6. Определение методической погрешности способа центрирования

Выше отмечалось, что при центрировании второго центра первый смещается с оси шпинделя. Величина смещения определяется графически. Разработанная методика этого построения приведена для двояковыпуклой линзы на Рис. 12. О₁O₂ – оптическая ось до центрирования, О – центр сферы патрона, ось патрона совпадает с осью шпинделя в системе координат XYZ, ось шпинделя совпадает с осью OX. Сначала смещаем патрон в плоскости YOZ так, чтобы совместить точку O₁ с точкой О. Ось патрона займет новое положение. Центр сферы патрона переместится в точку , центр кривизныO₂ переместится в точку . Вращая винты, поворачиваем сферическую часть патрона вокруг центрадля того, чтобы центр сферыO₂ из точки переместить на ось шпинделя в точку. При этом повороте первый центр кривизныO₁ из точки переместится в точку. Оптическая осьO₁O₂ не совпадает с осью вращения шпинделя, появится «неуточненная погрешность метода».

Построения сделаны для шести основных линз: двояковыпуклой, двояковогнутой, вогнуто-плоской выпукло-плоской, выпукло-вогнутые мениски.

Очевидно, что для уменьшения этой погрешности надо начинать центрирование с поверхности линзы, которая расположена точнее относительно оси шпинделя, или повторять весь процесс.

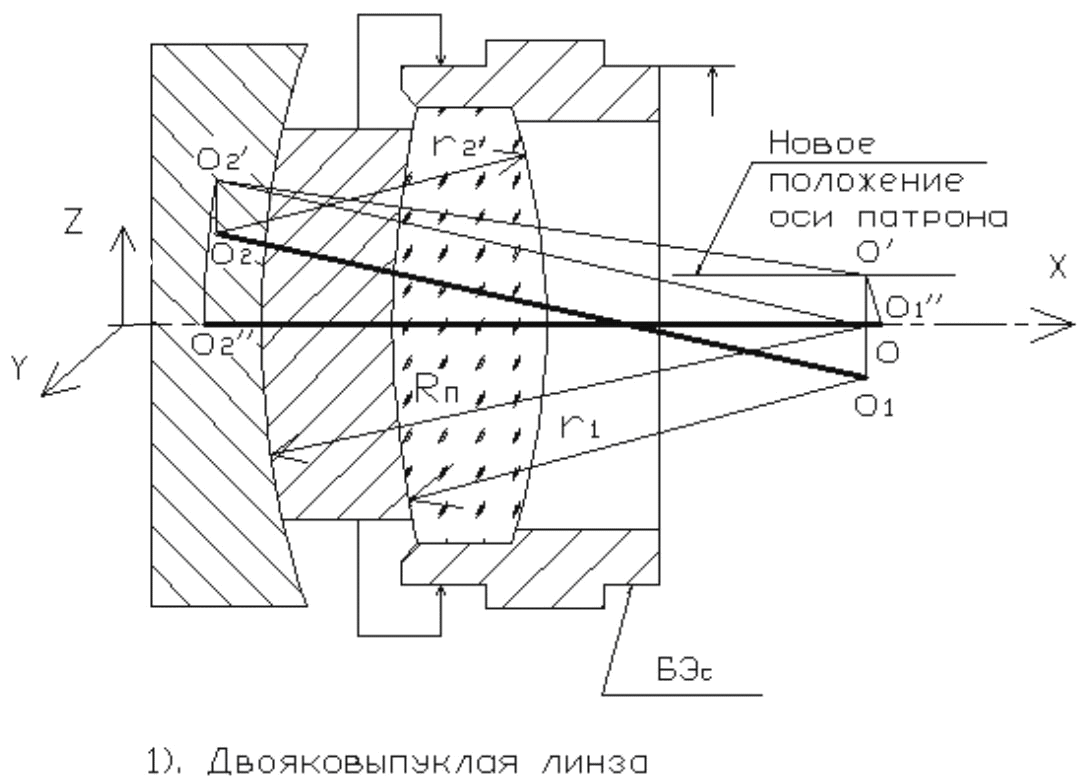
6)Поправить оси

Рис. 12. Схемы к определению методической погрешности метода центрирования.

7. Схемы к вычислению угла и расстояния между оптической осью и осью оправы Определение расстояния

Рис. 13. Схема к вычислению расстояния между оптической осью и осью оправы.

Как только установили в патроне оправу, включили освещение, посмотрели в окуляр, то сразу видим ось БЭ! Это ось зет, проходящая через перекрестие сетки микроскопа. Навели на О₂, померили О¹О₂, навели на О₁, померили О₁О и если в чертеже заданы эти отклонения, то известна полная картина погрешностей по расположению центров кривизны. Осталось измерить расстояние и угол между осями.

Ввели систему координат XYZ так, что плоскость XOY проходит через точку О₁.

Ось измерительного устройства совпадает с OZ; О₁ – центр сферы правой, О₂ –центр сферы левой, отрезки иопределяют децентрировку правой и второй поверхностей соответственно.

Расстояние междуиOZ строится в следующей последовательности. Плоскость XOY, перпендикулярна OZ, тогда расстояние определяется как расстояние между их ортогональными проекциями на эту плоскость (т.е.XOY). Ортогональная проекция OZ – это точка О, проекцию построим спроектировав точкуО₂ на XOY – это точка , значит– проекцияи перпендикулярOH – искомое расстояние. Вычислим это расстояние.

Векторизуем отрезки: ;

;

Уравнение :или общее уравнение прямой

.

Введем обозначения ;,

и тогда - общее уравнение прямой.

Расстояние от точки 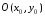до прямой:

. (2)

Определение угла

Перенесли параллельно себе OZ в точку (см. Рис. 14), тогда– искомый угол.

или (7)

Определение истинного расположения расстояния

Переносим параллельно себе отрезок до пересечения св точкеH, тогда 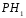– истинное положение расстояния междуиOZ. Видно, что

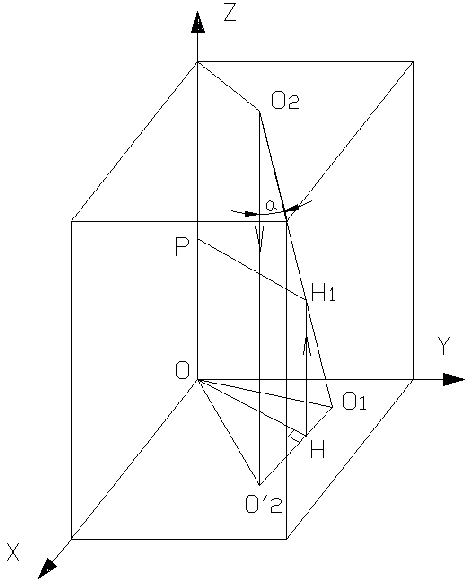
Рис. 14. Схема к вычислению угла между оптической осью и осью оправы.

Н₁НО₁ О₂О₂¹О₁,

тогда Н₁Н/О₂О₂¹ = Н₁О₁/О₂О₁ или Н₁Н = ОР = Н₁О₁ О₂О₂¹ / О₂О₁.