
- •Национальный исследовательский университет
- •Бакалавра
- •Национальный исследовательский университет
- •Содержание разделов задания и исходные данные
- •Перечень графического материала
- •Оглавление
- •Введение
- •1. Полупроводники
- •2. Квантовый размерный эффект электронов и дырок _
- •Квантоворазмерные гетероструктуры на основе твердого раствора AlxGa1-xAs
- •4. Модулированное легирование
- •5. Полупроводниковые материалы для квантовых ям и сверхрешеток.
- •5. Моделирование энергетического спектра электрона в твердом теле (модель Кронига-Пенни)
- •6. Моделирование энергетического спектра электрона в одномерной квантовой яме
- •5.2. С бесконечно высокими стенками
- •Оценка энергетического положения разрешенных состояний в симметричной кя конечной глубины.
- •Энергия в квантовой яме
- •2. Особенности движения частицнад потенциальной ямой
- •5.1.Зависимость числа уровней от ширины ямы
- •Применение квантовых наноструктур в электронике
- •Зонная структура формирования ямы, размерность, определение физических размеров квантовой ямы
- •Научная ценность моей работы.
Оценка энергетического положения разрешенных состояний в симметричной кя конечной глубины.
 (1.4.21)
(1.4.21)
Зависимости X(Y) для первых трех энергетических уровней, рассчитанные с использованием (1.4.21), приведены на рис. 1.3. По ним, задаваясь параметрами КЯ W, U0 и т (т.е. X), можно определить Y и энергетическое положение уровней. Видно, что для КЯ заданной ширины с уменьшением глубины U0 (т.е. X) будут происходить уменьшение энергии разрешенных состояний Y и последовательное выталкивание их из ямы (т.е. уровни будут сгущаться медленнее, чем уменьшается глубина ямы). Причем при изменении U0 от ∞ до Еп-1(∞,W) энергия n-го уровня в КЯ конечной глубины будет уменьшаться от En(∞,W) лишь до Еп-1(∞,W), а при дальнейшем уменьшении U0 п-й уровень будет вытолкнут из ямы.

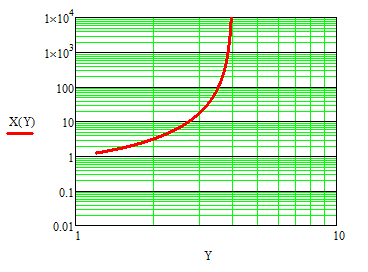

Рис. 1.3. Зависимости X(Y) для первых трех энергетических уровней с n = 1, 2 и 3 (кривые 1-3 соответственно), рассчитанные с использованием выражения (1.4.21)
Энергия в квантовой яме
Вычислим предварительно уровни энергии частицы в одиночной потенциальной яме Глубина и ширина ямы есть V0 и b соответственно. Введем следующие обозначения:
 (масса
частицы)
(масса
частицы)
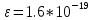 (энергия
частицы)
(энергия
частицы)
 (ширина
ямы)
(ширина
ямы)
 (глубина
ямы)
(глубина
ямы)
Нахождение уровней энергии в потенциальной яме.
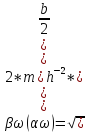

Рис. 1. Уровни энергии в потенциальной яме
Точки пересечения этой окружности с кривыми дают собственные значения энергии (в единицах Vo)






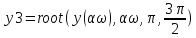




2. Особенности движения частицнад потенциальной ямой
Рассмотрим случай, когда полная энергия частицы Е меньше высоты стенок потенциальной ямы (финитное движение). Здесь размерный эффект проявляется в квантовании энергии и волнового вектора частицы.Когда энергия частицы превосходит высоту стенок потенциальной ямы (Е > U), движение частицы инфинитное. Однако, как и при движении над потенциальным барьером, здесь возможны отражение частиц от областей с резким изменением потенциала (в данном случае от краев ямы) и даже своеобразный резонансный захват пролетающих над ямой частиц.
Если частица движется вдоль оси X, то, достигая потенциальной ямы, она испытывает действие сил. При этом частица либо отразится, либо «пройдет» над потенциальной ямой.
5.1.Зависимость числа уровней от ширины ямы
В зависимости от ширины квантовой ямы, в ней может находится несколько уровней. На рис. 2.1 представлена зависимость ширины квантовой ямы и наличие числа уровней в ней. Высота ямы остается неизменна.

Рис. 2.1 Зависимость числа уровней от ширины ямы.
По размерам ям определяется возможность создания наноразмерных структур, позволяющих удерживать электроны. Определяются минимально возможные размеры квантовых приборов.
Применение квантовых наноструктур в электронике
Резонансный туннельный диод.
В классической физике если полная энергия частицы меньше потенциальной энергии в области барьера, то эта частица отражается и затем движется в обратном направлении. В том случае, когда полная энергия превышает потенциальную, барьер будет преодолен. Квантовая частица ведет себя иначе: она преодолевает барьер подобно волне. Даже если полная энергия меньше потенциальной, есть вероятность преодолеть барьер. Это квантовое явление получило название "туннельный эффект". Оно используется в резонансном туннельном диоде.
Он состоит из двух барьеров, разделенных областью с малой потенциальной энергией. Область между барьерами – это как бы потенциальная яма, в которой есть один или несколько дискретных уровней. Характерная ширина барьеров и расстояние между ними составляют несколько нанометров. Области слева и справа от двойного барьера играют роль резервуаров электронов проводимости, к которым примыкают контакты. Электроны занимают здесь довольно узкий энергетический интервал. В приборе используется следующая особенность двойного барьера: его туннельная прозрачность имеет ярко выраженный резонансный характер. В том случае, когда энергия электронов, налетающих на барьеры, равна энергии дискретного уровня, туннельная прозрачность резко возрастает. При резонансе из-за интерференции волн во внутренней области гасится волна, отражающаяся от двойного барьера. Следовательно, волна, упавшая слева, полностью проходит направо.
Рассмотрим, как работает резонансный диод. Ток, протекающий через двойной барьер, зависит от величины приложенного напряжения. Потенциал в приборе падает главным образом в области двойного барьера, так как области слева и справа от него обладают высокой проводимостью. Если приложенное напряжение мало и энергия электронов, налетающих на барьер слева, меньше энергии дискретного уровня, то прозрачность барьера и, следовательно, протекающий ток будут малы. Ток достигает максимального значения при таких напряжениях, когда энергия электронов равна энергии дискретного уровня. При более высоких напряжениях энергия налетающих электронов станет больше энергии дискретного уровня и туннельная прозрачность барьера уменьшится. При этом ток также уменьшится. На вольтамперной характеристике будет участок отрицательного дифференциального сопротивления. Благодаря этому в электронных схемах резонансный диод может использоваться не только как выпрямитель, но и выполнять самые разнообразные функции. Если к центральной области резонансного диода подвести контакт, через который можно управлять положением дискретного уровня, получится новый прибор – транзистор.
Не разобрано/пометки/нужное

