Оценка случайных погрешностей

Случайные погрешности трудно устранить. Они проявляются в рассеивании результатов многократных измерений одной и той же величины.

Оценку случайных погрешностей производят с помощью теории вероятности и математической статистики.

Нормальный закон распределения (закон Гаусса)

Этот закон является одним из наиболее распространенных законов распределения погрешностей, что объясняется центральной предельной теоремой теории вероятностей.

Центральная предельная теорема ТВ - распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа неравномерно действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Пример:

1. равноценные (50х50)

2. неравноценные (если событий >5)

3. незначительные по сравнению с сумарным действием.

Закон Гаусса имеет следующее выражения:

MX- математическое ожидание, оно является центром группирования результатов наблюдения.

G- среднеквадратичное отклонение характеризует величину рассеивания результатов наблюдений, т.е. точность измерения.

Дисперсия – математическое ожидание квадрата отклонения случайной величины от квадрата ее математического ожидания.

- смещенная характеристика дисперсии.

- несмещенная характеристика дисперсии.

Так как среднее арифметическое вычисляется по результатам отдельных наблюдений, то является тоже случайной величиной и характеризуется своим эмпирическим средне квадратическим отклонением

68% - доверительная вероятность в этом интервале лежат 68% всех размеров, среднеквадратическое отклонение является 68% или доверительным интервалом.

95% - в промышленности 99.73% - в научных исследованиях

Доверительный интервал, интервал в котором мы ожидаем размер.

Доверительная вероятность - вероятность того, что размеры деталей или результаты измерения окажется внутри доверительного интервала.

За оценку случайной погрешности результата измерений принимают доверительный интервал среднего арифметического.

Случайные погрешности, > 3G, считаются грубыми и исключаются из результата измерения.

При малом nиспользуют коэффициент Стьюдента, где

При nраспределение Стьюдента переходит в нормальное распределение, чем большеn, тем меньше коэф. Стьюдента, интервал с заданной вероятностью уменьшается

,P= , n=

№8

1. Посадки с натягом. Схемы расположения полей допусков в системе отверстия и вала. Применение посадок с натягом и примеры обозначения на чертежах.

2. Высотные параметры шероховатости поверхности. Нормирование и примеры обозначения на чертежах шероховатости поверхности с использованием высотных параметров.

3. Нормирование точности метрической резьбы. Примеры обозначения на чертежах посадок резьбовых соединений с зазором.

Система допусков и посадов метрических резьб

Внутренние и наружные резьбы соединяются по боковым сторонам профиля. Возможность контакта по вершинам и впадинам резьбы исключается соответствующим расположением полей допусков по и. В зависимости от характера сопряжения по боковым сторонам профиля (т.е. по среднему диаметру) различают резьбы со скользящей посадкой, с зазором, натягом и с переходными посадками.

Система допусков и посадок метрической резьбы регламентирована СТТ СЭВ 640-77, предусматривающим допуски посадок скольжения и с зазором.

1. Степени точности резьбы. Допуски диаметров резьбы устанавливаются степенями точности, обозначенные цифрами: с 3 по 9

	Степени точности
Диаметры наружной резьбы Наружный d Средний d2	4; 6; 8 3; 4; 5; 6; 7; 8; 9
Диаметры внутренней резьбы Внутренний D1 Средний D2	4; 5; 6; 7; 8 4; 5; 6; 7; 8

Допуск внутреннего диаметра d₁ наружной резьбы и наружного диаметра D внутренней резьбы не устанавливаются.

Допуски среднего диаметра являются суммарными.

2. Допуски резьбы. Основным рядом допусков для всех диаметров, в соответствии с рекомендацией JSO, принят ряд по 6-1 степени точности. Допуски диаметров резьбы для 6-ой степени точности при нормальной длине свинчивания определяются формулам.

Например, для d₂

Для D₂

где Р – в мм, D – среднее геометрическое крайних значений интервалов номинальных диаметров; Т – в мкм.

Допуски остальных степеней точности определяются умножением допуска 6-1 степени точности, найденного по соответствующим формулам, на коэффициенты. Например

Степень точности	3	4	5	7	8	9
Коэффициент	0,5	0,63	0,8	1,25	1,6	2

Из формулы (1) следует, что допуск на 1/3 больше допускапри одной и той же степени точности.

3. Поле допусков резьбы. Положение поля допуска диаметра резьбы определяется основным отклонением (верхним es для наружной резьбы и нижним EJ для внутренней). Для получения посадок резьбовых деталей с зазором предусмотрено 5 основных отклонений для наружной и 4 для внутренней резьбы. Эти отклонения одинаковы для d; d₂ и D₁; D₂. Выбранная величина основного отклонения соблюдается единой по всему периметру профиля, т.е. распространяется и на ненормируемые d₁ и D.

Большие отклонения d, e, f, E, F, G преимущественно назначают для резьб с защитными покрытиями.

О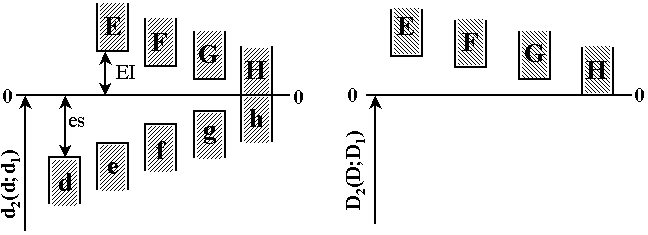тклонения отсчитываются от номинального профиля резьбы в направлении, перпендикулярном оси резьбы.

Поле допуска диаметра резьбы образуется сочетанием допуска и основного отклонения.

Поле допуска резьбы образуется сочетанием поля допуска среднего диаметра с полем допуска диаметра выступов (наружного диаметра для наружной резьбы и внутреннего диаметра D₁ для внутренней резьбы).

Поля допусков резьбы устанавливаются в классах точности – точный, средний и грубый – в зависимости от длины свинчивания.

Длина свинчивания. Для выбора степени точности в зависимости от длины свинчивания установлены три группы свинчивания: S – короткие, N – нормальные и L - длинные.

К нормальной (N) длине свинчивания относятся длины свыше 2,24Pd^0,2 до 6,7Pd^0,2. Длины свинчивания меньше нормальной, относятся к группе S, а больше – к группе L.

Классы точности резьбы. В соответствии со сложившейся во многих странах практикой поля допусков сгруппированы в 3 классах точности: точном, среднем и грубом.

Понятие о классах точности условное (на чертежах указывают не классы, а поля допусков), оно используется для сравнительной оценки точности резьбы.

Точный класс – для ответственных статически нагруженных резьбовых соединений.

Средний класс - для резьб общего применения.

Грубый класс – при нарезании резьбы в длинных глубоких отверстиях.

№9