Важные термины параметрического моделирования в MicroStation
Ограничение - это геометрическая информация, которая ограничивает или управляет каким-либо элементом конструкции.
Элементы параметрической модели - это элементы (точка, бесконечная линия, окружность, эллипс или В-сплайновая кривая), которые дают возможность ограничениям локализовать место расположения, ограничить или упорядочить другие элементы. Например, линия, как элемент модели, может быть осевой линией для какого-либо симметричного проекта.
Определенная модель - набор элементов параметрической модели, которые полностью определяются ограничениями или являются постоянными и не имеют никаких дополнительных ограничений. При этом, возможно имеется более одного реализуемого решения для набора элементов модели, которые полностью определены, но желаемый выборобычноясен.
Не доопределенная параметрическая модель - набор элементов модели, который полностью не определен ограничениями и не является постоянным. Элемент модели, который не доопределен, имеет много возможных «решений» и неоднозначен.
Избыточное ограничение - ограничение, которое применяется к набору элементов модели, который уже является определенным. Избыточное ограничение может быть, а может и не быть в противоречии с другими ограничениями, но в любом случае, оно не несет никакой полезной информации.
Степени свободы - число, которое показывает степень неоднозначности (недоопределенности) параметрической модели.
Обновление ограничений - решение алгебраических уравнений, описывающих конструкцию для заданного набора ограничений и показ степени свободы модели (DOF - Degree of freedom) и возможные места для ее полного определения.
Символы ограничений - это элементы, которые относятся к классу Построения и имеют специальное изображение для каждого типа ограничений, размер символов ограничений управляется в установках размера текста.
Ограничения параметрической модели
Ограничения указывают на то, какие характеристики должна иметь параметрическая модель, но не как получить ее в проекте с этими характеристиками. Как вычислить
46
конкретные геометрические параметры в свете этих ограничений - это задача обновления ограничений конструкции.
Большинство связей ограничения относится к основной части или к общей структуре параметрической модели. Детали проекта располагаются и формируются в этой структуре. Например, если параметрическая модель является симметричной, то он имеет элементы конструкции и ограничения, которые некоторым способом связывают элементы с осевой линией.
Ограничения накладываются с использованием инструментальных средств, которые содержит инструментальная панель Ограничения.
Можно создать следующие типы ограничений:
Расположения - ограничение, которое устанавливает расположение некоторой точки в плоскости проекта.
Геометрическое - ограничение, которое управляет положением или ориентацией двух или более элементов относительно друг друга.
Размерное - ограничение, которое управляется размером. Алгебраическое - уравнение, которое выражает связь между переменными.
Когда какое-либо ограничение добавляется, изменяется или удаляется, то модель решается заново, т.е. делается попытка восстановления параметрической модели так, чтобы новое или изменяемое ограничение, также как все существующие ограничения, было удовлетворено. Если какое-либо решение найдено, то соответствующие изменяемые элементы обновляются и повторно показываются. Полученное решение может воздействовать на элементы, которые не связаны с новым ограничением очевидным образом или локально.
Если решение невозможно, то выводится сообщение о невыполнении данной операции и иногда показывается графически место возникновения проблемы. Геометрия проекта не обновляется, но это ограничение принимается в любом случае. Если MicroStation Edition 2004 сообщает о невыполнении какой-либо операции, даже если новое ограничение не является избыточным и Вы уверены, что решение фактически возможно, то графические указатели могут помочь перестроить геометрию модели наиболее близко к предполагаемому решению и затем выполнить решение заново.
Добавление нового ограничения уменьшает неоднозначность параметрического фрагмента. (Удаление ограничения дает противоположный эффект.)
Ограничение может применяться только к элементу параметрической модели. Когда ограничение применяется к какому-либо элементу файла проекта, то он преобразуется в эквивалентный элемент параметрической модели.
47
Названия некоторых ограничений могут предполагать одностороннюю зависимость одного элемента от другого. Фактически же все ограничения устанавливают двухсторонние связи между элементами.
Большинство ограничений расположения и геометрических ограничений назначается в классе элементов - Построения. Кроме того, можно определять слой и класс размерных ограничений, ограничений расположения и алгебраических ограничений. В будущем будет добавлена возможность определять слой, символику и класс для всех ограничений и элементов параметрической модели.
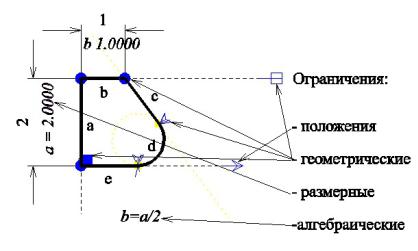
Рис. 2. Плоская параметрическая геометрическая модель.
Пример параметрической модели на рис. 2. состоит из пяти геометрических элементов моделирования (a, b, c, d и e). Объявленные ограничения между элементами обозначены символически на рисунке и подразумевают следующее:
Отрезок e горизонтален и касается дуги e. Отрезок a перпендикулярен e и имеет длину a=2.0. Отрезок b параллелен отрезку e и имеет длину b.
Отрезок c связан с отрезком b общей точкой пересечения и касается дуги e. Линия d - круговая дуга, касательная к отрезкам c и e.
Задано алгебраическое ограничение b=a/2.
Заданы точки пересечения отрезков e и a, а также a и b.
Эта модель не доопределена и число степеней свободы этой модели равно 2, т.е. необходимо добавить еще два ограничения.
Зачатки параметризации, которую можно назвать жесткой, процедурной параметризацией, были реализованы еще в обычных чертежных системах, типа AutoCAD. Эти системы сохраняют последовательность построения геометрических моделей в форме процедуры, закодированной в некотором внутреннем представлении. Фактически это ве-
48
дет к представлению геометрической модели чертежа как последовательности определений геометрических элементов, где каждое определение в последовательности вычисляет значение параметров текущего элемента как функции параметров уже вычисленных элементов и некоторых входных параметров. В некоторых системах, такую процедуру можно было непосредственно отредактировать или же написать ее заново, используя текстовое описание этой процедуры, а затем повторно ее интерпретировать. В таких процедурных параметрических системах можно было осуществлять только небольшой диапазон изменений геометрических моделей. Жесткая последовательность определений параметров модели означала, что добавление новых типов зависимостей между элементами модели было весьма затруднительно. Следовательно, многократное использование существующих моделей как основы получения новых подобных моделей в такой реализации было практически невозможно.
В связи с этим были разработаны гибкие параметрические/вариационные системы геометрического моделирования, в которых жесткая последовательность определений параметров элементов, заменена некоторой общей процедурой, которая не привязана к первоначальной последовательности операций геометрического моделирования, используемых при первоначальном построении геометрической модели. Эти системы используют некоторый тип декларативного представления ограничений, вместо процедурного и используют графы ограничений и логику предикатов первого уровня. Для изменения модели в таких системах, сначала редактируются ограничения, а затем выполняется общий алгоритм удовлетворения ограничений, чтобы разрешить отредактированные отношения между параметрами геометрических моделей элементов. Различие между параметрическими и вариационными методами заключается только в типе алгоритма удовлетворения ограничений, используемого этими системами.
Параметрические системы геометрического моделирования удовлетворяют ограничения, выполняя последовательно назначения переменных модели, при этом каждое новое значение параметров геометрической модели вычисляется как функция предварительно назначенных значений параметров. В отличие от процедурных систем, порядок назначений является гибким и определяется алгоритмом удовлетворения ограничений.
Вариационные системы геометрического моделирования удовлетворяют ограничения путем формирования системы уравнений, представляющих ограничения и удовлетворяют все ограничения модели одновременно путем численного решения соответствующей системы нелинейных алгебраических уравнений.
Различие между параметрическими и вариационными системами можно продемонстрировать на следующих простых примерах определения переменной x:
49
x = |
−b ± |
(b2 −4ac) |
- явное уравнение. |
|
2a |
||
|
|
|
ax2 +bx +c =0 - неявное уравнение.
С помощью явного уравнения можно непосредственно вычислять значение переменной x при заданных параметрах a, b и c и знаке квадратного корня. Параметрическая система работает, просматривая ограничения и выполняя предопределенные явные методы решения.
Напротив, вариационная система использует неявное уравнение, которое должно быть "решено" для x, при этом возможны несколько решений. Оба метода имеют преимущества и недостатки. Основанные на явном последовательном удовлетворении ограничений, параметрические модели работают быстро. Однако они не могут учесть взаимно связанные ограничения. С другой стороны, вариационные модели, используя неявные методы удовлетворения ограничений, могут обрабатывать связанные ограничения, но они менее быстрые и более ограничены при обработке не полностью определенных или противоречивых моделей, поэтому на практике в параметрическом моделировании используют оба метода.
50