
- •Глава 2. Электрические цепи однофазного синусоидального тока.
- •2.1. Синусоидальный ток и основные характеризующие его величины.
- •2.2. Среднее и действующее значение синусоидальных тока и эдс.
- •2.3. Сложение синусоидальных функций времени. Векторные диаграммы. Основы символического метода расчета.
- •2.4. Пассивные элементы электрической цепи.
- •2.5. Резистивный элемент.
- •2.9 Параллельные соединения элементов r, l, c.
- •2.9.1. Мощность в цепи синусоидального тока. Комплексная мощность.
- •2.10. Законы Кирхгофа и уравнение энергетического баланса в комплексной форме.
- •2.11. Резонанс в цепях синусоидального тока.
- •2.11.1. Резонанс напряжений.
- •2.11.2. Резонанс токов.
- •2.12. Резонанс напряжений и токов в разветвленных цепях.
2.10. Законы Кирхгофа и уравнение энергетического баланса в комплексной форме.
Первый закон Кирхгофа:
![]()
Второй закон Кирхгофа:

Уравнение энергетического баланса:
![]() .
.
![]() .
.
![]() .
.
2.11. Резонанс в цепях синусоидального тока.
Реактивные
сопротивления и проводимость являются
частотно-зависимыми величинами.
Следовательно, при последовательном
или параллельном соединении элементов
L
и C
возможна на какой-то частоте полная
компенсация реактивных сопротивлений
или проводимостей. Режим, при котором
наступает компенсация, называют
резонансом. При резонансе входное
сопротивление цепи становится активным,
входное напряжение совпадает по фазе
с входным током, а полная мощность будет
активной. Угловая частота,
![]() ,
при которой наступает резонанс, называется
резонансной или собственной угловой
частотой цепи. Различают две разновидности
резонанса: резонанс напряжений и резонанс
токов.
,
при которой наступает резонанс, называется
резонансной или собственной угловой
частотой цепи. Различают две разновидности
резонанса: резонанс напряжений и резонанс
токов.
2.11.1. Резонанс напряжений.
Может возникнуть в цепи с последовательным соединением L и C, рис. 2.20а.
 Для
этой цепи запишем:
Для
этой цепи запишем:
![]() .
.
Условие резонанса:
![]() или
или ![]() ,
,
откуда
резонансная частота
 .
.
Настройку цепи в резонанс, изменение параметров цепи при частотах , отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r, L, C.
На
рис. 2.20б,в,г приведены частотные
характеристики реактивных сопротивлений
![]() и
и![]() ,
суммарного реактивного сопротивления
,
суммарного реактивного сопротивления![]() ,
модуля полного сопротивления
,
модуля полного сопротивления ,
модуля входного тока
,
модуля входного тока![]() ,
а также амплитудно-частотные характеристики
напряжений:
,
а также амплитудно-частотные характеристики
напряжений:
![]() ,
,
![]() ,
,
![]() .
.
По
графику
![]() определена резонансная частота
определена резонансная частота![]() ,
по графику
,
по графику![]() можно увидеть, что сопротивление цепи
при резонансе минимально и равно
активному сопротивлению, по графику
можно увидеть, что сопротивление цепи
при резонансе минимально и равно
активному сопротивлению, по графику![]() - что ток в цепи при резонансе максимален.
Графики
- что ток в цепи при резонансе максимален.
Графики![]() ,
,![]() ,
,![]() имеют ярко выраженный избирательный
характер, т.е. имеют максимальные значения
на резонансной частоте или вблизи нее.
Можно также отметить, что напряжения
имеют ярко выраженный избирательный
характер, т.е. имеют максимальные значения
на резонансной частоте или вблизи нее.
Можно также отметить, что напряжения![]() и
и![]() при резонансе могут превышать значение
входного напряжения. Это хорошо
иллюстрируется с помощью векторных
диаграмм напряжения приведенных на
рис. 2.20д,е,ж при частотах
при резонансе могут превышать значение
входного напряжения. Это хорошо
иллюстрируется с помощью векторных
диаграмм напряжения приведенных на
рис. 2.20д,е,ж при частотах![]() ,
,![]() и
и![]() .Обратите
также внимание на значения угла
.Обратите
также внимание на значения угла![]() на этих частотах и сопоставьте эти
значения с характером реактивных
сопротивлений на соответствующих
частотах. Так при частотах
на этих частотах и сопоставьте эти
значения с характером реактивных
сопротивлений на соответствующих
частотах. Так при частотах![]() ,
реактивное сопротивление носит емкостной
характер и
,
реактивное сопротивление носит емкостной
характер и![]() и
т.д.
и
т.д.
2.11.2. Резонанс токов.
Возможен в цепях с параллельным соединением L и C элементов, рис. 2.21а.
 Для
этой цепи запишем уравнение по первому
закону Кирхгофа:
Для
этой цепи запишем уравнение по первому
закону Кирхгофа:

Компенсация реактивных проводимостей и реактивных токов:
![]()
 ,
,
произойдет
на резонансной частоте
![]()
Для
анализа явления резонанса токов построим
частотные характеристики реактивных
проводимостей рис.2.21б, модуля полной
проводимости
![]() ,
рис.2.21в, модуля полного тока
,
рис.2.21в, модуля полного тока![]() ,
рис. 2.21г. Здесь отмечена резонансная
частота, полная проводимость цепи при
резонансе минимальна и полный ток
минимален. Векторные диаграммы токов,
построенные для частот
,
рис. 2.21г. Здесь отмечена резонансная
частота, полная проводимость цепи при
резонансе минимальна и полный ток
минимален. Векторные диаграммы токов,
построенные для частот![]() ,
,![]() ,
,![]() ,
рис. 2.21д,е,ж, позволяют убедиться, что
токи в катушке и конденсаторе могут
значительно превышать полный ток.
,
рис. 2.21д,е,ж, позволяют убедиться, что
токи в катушке и конденсаторе могут
значительно превышать полный ток.
2.12. Резонанс напряжений и токов в разветвленных цепях.
Мы рассмотрели резонанс в последовательном и параллельном контурах с идеальными элементами L и C. Рассмотрим другие более сложные примеры. Для цепи рис. 2.22 запишем условие резонанса, определим резонансную частоту и ток в цепи.

Входные сопротивления цепи:
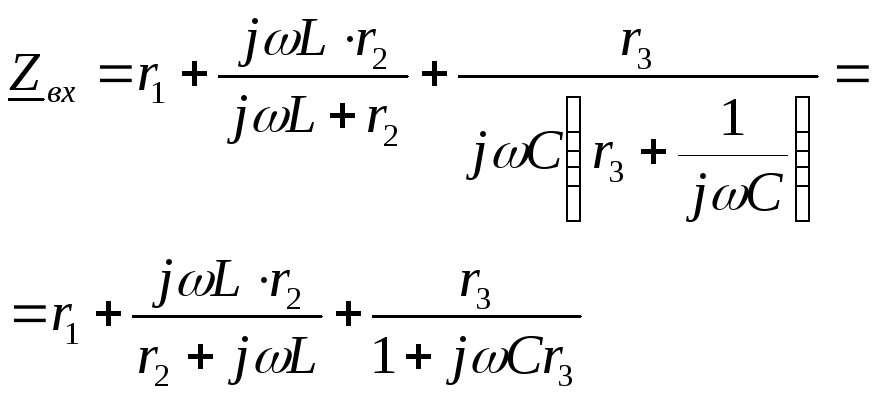
Выделим действительные и мнимые части сопротивлений:

Компенсация
реактивных сопротивлений произойдет
на частоте
![]() :
:

Входное сопротивление при резонансе минимально и равно:

Входной
ток при резонансе максимален и равен


Для цепи, приведенной на рис. 2.23, возможен резонанс токов. Запишем входную проводимость цепи
![]()
Выделим действительные и мнимые части проводимостей:

Условие резонанса:

Входной ток:

В разветвленных цепях с L и C возможны несколько резонансов. Так в цепи рис. 2.24 возможны и резонанс токов в ветвях L , C и резонанс напряжений для всей цепи.

Пример.
Цепь,
рис 2.25 настроена в резонанс. Определить
![]() и
и
![]() ,
если задано:
,
если задано:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Решение:
Входное сопротивление цепи равно:

Условие резонанса напряжений:


Решая
квадратное уравнение относительно
![]() ,
получим
,
получим![]()
Ток при резонансе равен:

