2.9 Параллельные соединения элементов r, l, c.
Для схемы рис. 2.11. составим уравнение по первому закону Кирхгофа для мгновенных значений:
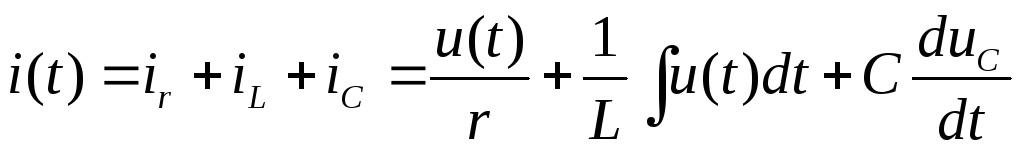(10)
Если
, то
(11)
Здесь
-
активная проводимость,
-
индуктивная проводимость.
Единица измерения проводимостей - сименс (Сим).
Векторная диаграмма токов приведена на рис. 2.12.
Уравнение (11) в комплексной форме:
(12)
Здесь
-
комплексная проводимость или комплекс
проводимости,
-
модуль комплекса проводимости
-
фаза комплекса проводимости.
Проводимости
образуют треугольник проводимости,
рис. 2.13.
Комплексная векторная диаграмма токов для уравнения (12) приведена на рис. 2.14.
Пример 1.
Для схемы, приведенной на рис. 2.15.
Задано:
,
L=6,37 мГн, С=796 мкФ, f=50 Гц,
,
,
Определить токи.
Решение.
Воспользуемся комплексным методом расчета. Запишем комплексы сопротивлений для каждой ветви:
,
.
Входное сопротивление цепи:
Входной
ток:
Определим
токи
и
Мгновенные значения токов запишем в виде:
Пример 2.
Для
схемы рис. 2.11 определить сдвиг по фазе
между входным током и напряжением, если
Ом,
Ом,
Ом.
Решение:
комплекс тока:
Фаза
напряжения принята за ноль, а фаза тока
получилась равной
.
Сдвиг по фазе между током и напряжением
.
2.9.1. Мощность в цепи синусоидального тока. Комплексная мощность.
Пусть
в цепи рис. 2.7 ток равен
.Мгновенное
напряжение будет сдвинуто по отношению
к току на угол
,
отличный от 0 и
.Мгновенная
мощность для этой цепи примет вид:
(13)
Выразим
сопротивления r
и
через модуль сопротивленияZ
:
, 
, 
(14)
Подставим (14) в (13), получим
Временные
диаграммы i(t),
u(t),
p(t)
приведены на рис. 2.16.
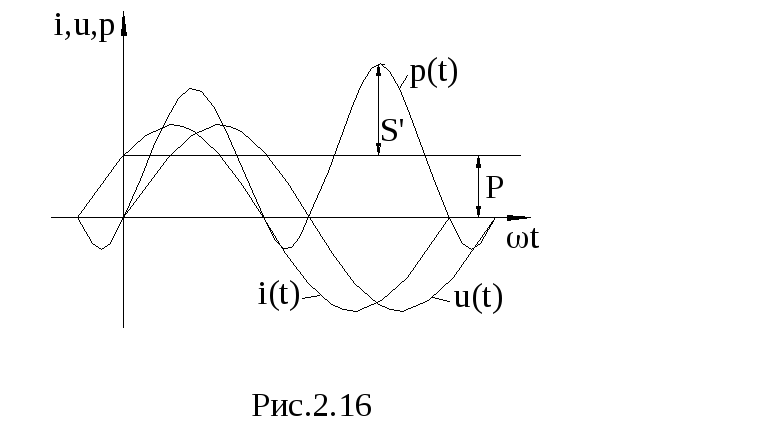
Мощность p(t) имеет постоянную составляющую, т.е. среднюю мощность, или активную мощность:
и
переменную составляющую. Амплитуда
переменной составляющей
называется полной мощностью, измеряется
в вольт-амперах, (ВА).
Мощности P и S связаны по закону треугольника мощностей, рис 2.17.
Третья
составляющая в этом треугольнике –
мощность реактивная
.
Реактивная
мощность измеряется в вольт-амперах
реактивных,(
).Полезная
мощность измеряется ваттметром.
Пример.
График
мгновенной мощности p(t)
приведен на рис. 2.19.
Максимальное и минимальное значения мощности соответственно равны 800 и 200 ВА. Определить полную активную и реактивную мощности цепи.
Решение:
Размах
значений мощности 1000
ВА, амплитудное
значение 500 ВА, это полная мощность S.
Среднее значение мощности P=800-500=300
Вт. Реактивная
мощность
.
Отношение активной мощности к полной (рис. 2.17) равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности
Для лучшего соотношения между мощностью электрической машины и других приборов и их габаритными размерами коэффициент мощности стремятся сделать максимально возможным.
Высокий коэффициент мощности желателен для уменьшения потерь при передаче энергии по линиям.
Чтобы выразить мощность через комплексы токов и напряжений воспользуемся следующим соображением.
Пусть
заданы комплексы
и
.
Активная
мощность должна быть равна
,
где
.
Отсюда следует, что при определении комплекса мощности фаза тока должна быть взята с обратным знаком, т.е. комплекс тока должен быть заменен на сопряженный.
Полная комплексная мощность
