Для первой гармоники

,

где ;

В общем случае , тогда,

а для первой гармоники ;

Для второй гармоники ;

Где ;

;

;

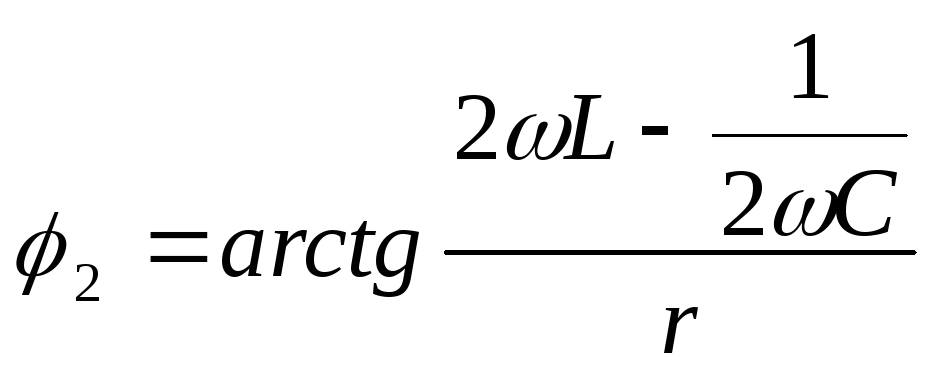
Напряжение U_r, резистивного элемента совпадает по фазе с током цепи и в общем случае:

, а так как ,то т.е. ,

где

Аналогично могут быть определены значения u_L и u_C :

;

.

Определение гармонических составляющих токов i₁ и i₂, а также напряжений U_r, U_L и U_C можно также осуществить с ис­пользованием комплексных чисел.

Пример 4.3. Несинусоидальная ЭДС - е(t) линейной электрической цепи рис. 4.6.а, изменяется по закону е(t)= 200 + 180sin(ωt - 30˚) + 120sin3ωt. Параметры цепи: r = 6 Ом, X_L=ωL= 2 Ом, X_С= 1/ωC=18 Ом. Определить мгновенное, действующее значение тока в цепи и действующее значение напряжения на участке цепи ab.

Решение. По отношению к постоянной составляющей ЭДС Е₀ = 200В сопротивление конденсатора равно бесконечности, т.е. X_C= 1/ωC = 1/ 0∙C= ∞. Следовательно, постоянная составляющая тока I_a= 0,

Расчет первой гармоники:

полное сопротивление цепи

угол сдвига фаз между ЭДС e₁ и током

20΄

так как , то

20΄

амплитуда и действующее значение первой гармоники тока

мгновенное значение тока

действующее значение напряжения на участке ab

Расчет третьей гармоники:

полное сопротивление цепи

т. е. для данной гармоники наблюдается резонанс напряжений, а, сле­довательно, угол сдвига фаз между ЭДС е₃ и током:

амплитуда и действующее значение тока

мгновенное значение тока

действующее значение напряжения на участке ab

Расчет общего тока:

мгновенное значение тока в цепи

действующие значения тока в цепи и напряжения на участке аb

В ряде случаев при проведении практических расчетов пе­риодические несинусоидальные ЭДС и напряжения представляют эквивалентными синусоидами. Подобная замена осуществляется так, чтобы действующее значение экви­валентной синусоиды ЭДС или напряжения равнялось действующему значению несинусоидальной величины.

4.6. Влияние резистивного, индуктивного и емкостного элементов цепи на форму кривой тока. Резонансные явления.

При резистивной нагрузке токи всех гармоник совпадают по фазе с соответствующими гармониками напряжений и форма кривой несинусоидального тока аналогична форме кривой напряжения u(t).

В цепи с индуктивным элементом амплитуда тока основной гармоники определяется как , а амплитуды токов всех после­дующих гармонических составляющих .

Так как сопротивление индуктивного элемента увеличивает­ся с переходом к высшим гармоникам, то амплитуда каждой гармоники тока будет уменьшаться обратно пропорционально порядку гармоники, и высшие гармоники тока будут проявлять­ся в меньшей степени в общей кривой тока. Таким образом, кривая тока меньше отличается от синусоиды, чем кривая на­пряжения. Аналогично в цепи с емкостным элементом амплитуды токов ос­новной и высших гармоник определяются как:

;

Так как сопротивление емкостного элемента уменьшается с переходом к высшим гармоникам, то амплитуды гармоник тока будут увеличиваться пропорционально порядку гармони­ки, форма кривой тока будет искажаться еще больше в сравне­нии с кривой напряжения.

Поскольку с ростом частоты сопротивление индуктивного элемента увеличивается, а емкостного уменьшается, в электри­ческой цепи рис.4.6,а может возникнуть резонанс напряжений либо для первой, либо для одной из высших гармоник. Усло­вие возникновения резонанса напряжений для некоторой k-гармоники

kωL = 1/kωC

При этом амплитуда тока резонансной гармоники может значительно превысить амплитуды тока всех остальных гармо­ник (см. пример 4.3), а на участках электрической цепи как с ин­дуктивным, так и с емкостным элементом могут возникнуть перенапряжения.

В электрических цепях несинусоидального тока при параллельном соединении катушки и конденсатора воз­можно возникновение резонанса тока либо для первой, либо для одной из высших гармоник с присущими данному резонан­су явлениями.

11