1.7. Уравнение баланса мощности в электрических цепях.

В любой электрической цепи сумма мощностей всех источников электрической энергии должна быть равна сумме мощностей всех приемников. На основании (1.11), (1.21..1.23),(1.25), можно записать в общем виде уравнение баланса мощности для любой электрической цепи

(1.26)

Чтобы уравнение баланса мощности давало более наглядное представление о характере энергетических процессов, целесообразнее составлять его для действительных направлений э.д.с., напряжений и токов.

1.8. Методы расчета электрических цепей.

Задача расчета электрической цепи ставится следующим образом. Задана схема электрической цепи, значения ее элементов и параметры источников. Требуется определить токи в ветвях и падение напряжения на элементах. Данная задача решается путем составления и решения системы уравнений, запись которых определяется выбранным методом расчета.

Перед составлением уравнений необходимо указать на схеме положительные направления известных и неизвестных величин.

1.8.1. Метод непосредственного использования законов Кирхгофа.

Данный метод целесообразен в следующих случаях:

- для расчета неразветвленных электрических цепей;

- если известна величина части токов, но неизвестны величины такого же количества источников или элементов цепи;

- для определения падения напряжения между какими-либо двумя точками электрической цепи;

- для проверки правильности расчетов, проведенных любым другим методом.

Проверка может быть также осуществлена путем составления уравнения баланса мощности.

З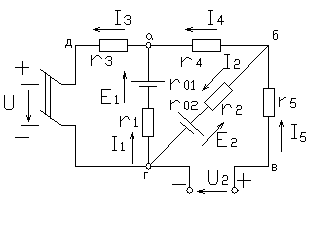адавшись положительными направлениями искомых величин, составляют уравнения сначала по первому закону Кирхгофа, максимальное число которых должно быть на единицу меньше числа узлов схемы. Недостающие уравнения следует составить по второму закону Кирхгофа.

В качестве примера составим систему уравнений для определения токов в

Рис 1.17 электрической цепи, схема которой изображена на рисунке 1.17 с известными сопротивлениями и величинами и направлениями источников э.д.с. и напряжений. Поскольку данная цепь имеет пять ветвей с неизвестными токами, необходимо составить пять уравнений. Выбрав положительные направления токов в ветвях, для узлов «а» и «б» составим уравнения по первому закону Кирхгофа, а для контуров «агда», «абга» и «бвгб» при обходе последних по часовой стрелке - уравнения по второму закону Кирхгофа.

1.8.2. Метод эквивалентных структурных преобразований.

В основе различных методов преобразования электрических схем лежит понятие эквивалентности, согласно которому напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными.

Преобразования электрических схем применяются для упрощения расчетов.

Рассмотрим наиболее типичные методы преобразования.

Последовательное соединение элементов.

При последовательном соединении элементов через них протекает один и тот же ток I (рис.1.18). Согласно второму закону Кирхгофа, напряжение, приложенное ко всей цепи

(1.27)

Для последовательного соединения сопротивлений r₁,r₂...r_n (рис. 1.18) с учетом (1.6) будем иметь

(1.28)

Ток в цепи с последовательным соединением элементов равен:

 

(1.29)

а напряжение на n-ом элементе равно

 

(1.30)

При последовательном соединении источников напряжения они заменяются одним эквивалентным источником с напряжениемUэкв, равным алгебраической сумме напряжений отдельных источников.

Рис 1.19 Причем со знаком «+» берутся напряжения, совпадающие с напряжением эквивалентного источника, а со знаком «-» - несовпадающие (рис.1.19).