Шпаргалки по ТОЭ 2
.docx|
1. Основные сведения прямом и обратном преобразовании Лапласа. 1. Прямое преобразование Лапласа: Пусть
функция
Обратным
преобразованием Лапласа называется
интегральный ряд
|
2. Свойства и теоремы преобразования Лапласа: 1. Свойство Линейности (однородности и аддитивности):
2. теорема дифференцирования:
3. теорема интегрирования: Если
4.
теорема
смещения в области
5. теорема о смещении во временной области:
6. предельные теоремы:
7.
теорема
подобия:
8.
Изображение
комплексной функции:
9. теорема интегрирования и диф. по параметру:
|
3. Законы Кирхгофа и схемы замещения в операторной схеме. 1.
Законы Кирхгофа в s-области:
2. Операторная схема замещения R-элемента: ВАХ:
3. Операторная схема замешения L-элемента: ВАХ:
схему замещения. Или по другому: АВХ:
Таким
образом в операторной схеме замещения
4. Операторная схема замещения С-элемента: АВХ ВАХ:
В зависимости от используемого метода решения (МУН, МКТ) используют наиболее подходящие варианты схем замещения. |
|
4. Расчет переходных процессов в цепях операторным методом. 1.
2.
3.
Переход в
Удобство:
относительная простота при повышении
порядка цепи
|
5.
Передаточная функция цепи и ее связь
с диф.ур.,
1.
Передаточная
функция:
4.
Частотные характеристики цепи формируем
из мередаточной функции с параметром
|
6. Периодические сигналы. Тригонометрические формы ряда Фурье. Периодическим
сигналом называется сигнал,
удовлетворяющий условию:
|
|
7. Ряд Фурье в комплексной форме. Рассмотри
sin-cos-форму
ряда Фурье:
иде
ряда Фурье: ло
экстрерумов.но
данным свойствам (1) имеет вид:
|
8. Дискретные характеристики периодического сигнала. Пусть
|
9. Использование преобразования Лапласа для расчета коэффициентов ряда Фурье и спектра периодического сигнала.
Рассмотрим
функцию
|
|
10. Мощность в установившимся периодическом режиме. Действующие значения токов и напряжений. Мощность или активная мощность определяется по формуле:
Указанные выражения для наглядности расчета представлены в виде:
|
Анализ установившихся периодических процессов в цепях. Считается,
что после коммутации переходный
процесс закончился и в цепи действует
вынужденный режим. При постоянных и
гармонических воздействиях вынужденный
режим называется установившимся. В
вынужденном режиме выходной сигнал
цепи имеет форму воздействия, поэтому
при периодических воздействиях
вынужденная составляющая реакции
тоже периодична. Ее расчет выполняется
следующим образом: 1) периодический
входной сигнал представляется в виде
отрезка ряда Фурье
|
111. Переход от периодических сигналов к апериодическим и отрядов Фурье к интегралу Фурье. Периодический
сигнал, удовлетворяющий условиям
Дирихле раскладываем в ряд Фурье:
|
|
12. Связь преобразования Лапласа с односторонним преобразованием Фурье. Пусть
функция
|
13. Спектральные характеристики апериодического сигнала, частотные характеристики с точки зрения спектра. Для
рассмотрения спектральных характеристик
апериодического сигнала используют
прямое преобразование Фурье.
|
|
|
14. Связь сплошного спектра одиночного импульса с дискретным спектром периодической последовательности импульсов этой же форму. Тут
типа графики функций
|
|
15. Ширина спектра и ее связь с длительностью и крутизной сигнала. Рассмотри
одиночный апериодический сигнал
Существуют
два сигнала одной формы, но разной
длительности. Данное изменение спектров
наблюдается на основе свойства
введенного преобразования Лапласа:
Крутой сигнал – сигнал, содержащий разрыв 1ого рода его производной с меньшим номером. |
|
16. Методы расчета сигнала по спектрам. 1)
пусть
по указанным спектрам определяем спектры периодического сигнала:
2)
Известен либо вещественный
|
|
|
|
Выражение
(3) и (4) называются тригонометрическими
формами преобразования Фурье. На
основе выражения (3) сигнал восстанавливается
с использованием мнимого спектра, а
на основе (4) – вещественного.
3) Связь вещественного апериодического спектра с преобразованием Лапласа
ВСЕ ЗАЕБАЛО!!! (14 jun 00:04) |
|
|
|
|
|
|

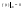 ,
,
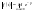 ,
где
,
где
 -
абсцисса сходимости. Указанный сигнал
преобразуем
по Лапласу следующем образом:
-
абсцисса сходимости. Указанный сигнал
преобразуем
по Лапласу следующем образом:
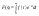 (1),
где
(1),
где
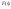 -
изображение, а
-
изображение, а
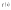 - оригинал.
- оригинал.
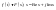 .
Выражение (1) – сходящийся интеграл,
а функция
.
Выражение (1) – сходящийся интеграл,
а функция
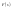 -
непрерывна и дифференцируема при
условии, что
-
непрерывна и дифференцируема при
условии, что
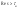 .
Из этого следует, что особые точки
.
Из этого следует, что особые точки
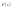 - корни знаменателя данной функции
при которых
- корни знаменателя данной функции
при которых
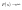 .
Эти точки располагаются в левой
полуплоскости относительно границы
.
Эти точки располагаются в левой
полуплоскости относительно границы
 .
.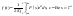 (2).
Для нахождения оригинала используем
не интеграл (2), а теорему о разложении,
согласно которой
(2).
Для нахождения оригинала используем
не интеграл (2), а теорему о разложении,
согласно которой
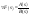 ,
где
,
где
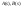 -
полиномы,
-
полиномы,
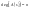 .
Полином
.
Полином
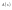 можно представить в виде произведения
с учетом корней:
можно представить в виде произведения
с учетом корней:
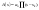 .
Таким образом
.
Таким образом
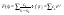
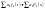
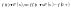 ,
логично что:
,
логично что:
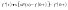 .
.
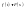 ,
то
,
то
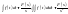 .
. :
: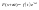 .
.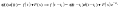 .
.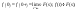 и
и
 .
.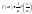 .
.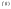 - комплексная функция, то
- комплексная функция, то

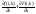 и
и
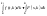
 ,
,
 .
.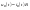 .
Согласно свойству однородности:
.
Согласно свойству однородности:
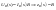 .
Сопротивление не зависит от
.
Сопротивление не зависит от
 .
.
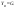 .
.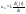 .
По т.Дифф.:
.
По т.Дифф.:

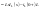 .
Изобразим для этого экв.
.
Изобразим для этого экв.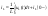 .
По т.Инт:
.
По т.Инт:
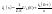 .
. -
элемент щамещается двумя элементами:
сопротивлением и независимым источником
(ИН, ИТ).
-
элемент щамещается двумя элементами:
сопротивлением и независимым источником
(ИН, ИТ).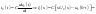
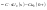 .
Схема выглядит так:
.
Схема выглядит так: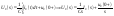 .
.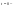 (режим
до коммутации). Если в цепи постоянное
воздействие
(режим
до коммутации). Если в цепи постоянное
воздействие
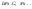 .
Находим
.
Находим
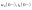 .
. (после
коммутации). Составляется операторная
схема замещения цепи на основе
операторных схем замещения
(после
коммутации). Составляется операторная
схема замещения цепи на основе
операторных схем замещения
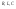 -элементов
(в цепи дополнительно появляются либо
ИН, либо ИТ, которые зависят от
-элементов
(в цепи дополнительно появляются либо
ИН, либо ИТ, которые зависят от
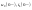 ).
В полученной схеме рассчитываются
изображения реакций.
).
В полученной схеме рассчитываются
изображения реакций. -область.
По найденным изображениям находят
образы реакций.
-область.
По найденным изображениям находят
образы реакций.
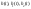 .
.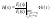 .
Передаточная функция определяется
как реакция цепи, изображенной в
операторной области с ННУ и в качестве
входного сигнала используется значение
«1» (изображение
.
Передаточная функция определяется
как реакция цепи, изображенной в
операторной области с ННУ и в качестве
входного сигнала используется значение
«1» (изображение
 ).
2.
Для нахождения импульсной характеристики
необходимо использовать теорему о
разложении поскольку
).
2.
Для нахождения импульсной характеристики
необходимо использовать теорему о
разложении поскольку
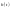 есть
оригинал передаточной функции и
использовать обратное преобразование
Лапласа. 3.
есть
оригинал передаточной функции и
использовать обратное преобразование
Лапласа. 3.
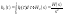
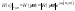
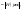
 5.
Связь
5.
Связь
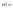 с
диф.ур. цепи:
с
диф.ур. цепи:
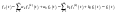 .
Используем т.Диф. при ННУ:
.
Используем т.Диф. при ННУ:
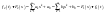 ,
,
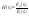 .
Сл-но: Нули
.
Сл-но: Нули
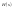 -значения
-значения
 при
которых
при
которых
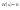 .
Полюсы – при котых
.
Полюсы – при котых
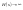 .
Полюсы должны совпадать с корнями
хар. поем
из мередаточной функции с параметром
азложении поскольку
линома
цепи.
.
Полюсы должны совпадать с корнями
хар. поем
из мередаточной функции с параметром
азложении поскольку
линома
цепи.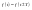 .
Пусть периодические сигнал удовлетворяет
условию Дирихле: 1) сигнал непрерывен
и может иметь
.
Пусть периодические сигнал удовлетворяет
условию Дирихле: 1) сигнал непрерывен
и может иметь
 разрыва
1ого рода. 2) на периоде сигнал ограничен
и имеет конечное число экстремумов.
Тогда он может быть представлен в виде
ряда Фурье:
разрыва
1ого рода. 2) на периоде сигнал ограничен
и имеет конечное число экстремумов.
Тогда он может быть представлен в виде
ряда Фурье:
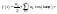
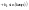 -
sin-cos-форма
записи, где
-
sin-cos-форма
записи, где
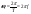 ,
,
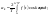
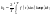
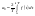 .
Из sin-cos-формы
можно перейти в cos-форму:
.
Из sin-cos-формы
можно перейти в cos-форму:
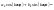

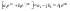 ,
где
,
где
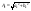 ,
,
 ,
т.о.
,
т.о.
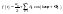 .
.
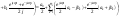 (1).
На основе следующих равенств:
(1).
На основе следующих равенств:
 и
и
 получаем
свойства, что
получаем
свойства, что
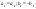 .
Согласчаем
свойства, что тв: орме.
.
Согласчаем
свойства, что тв: орме.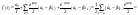
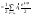 ,
где
,
где
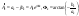 .
.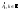 - комплексный спектр сигнала
- комплексный спектр сигнала
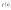 .
.
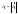 -
амплитудный спектр.
-
амплитудный спектр.
 -
фазовый спектр. Указанные спектры
являются функциями и изображаются в
следующем виде. В соответствии с
указанными свойствами построения
спектров периодических сигналов
-
фазовый спектр. Указанные спектры
являются функциями и изображаются в
следующем виде. В соответствии с
указанными свойствами построения
спектров периодических сигналов
 выполнялся
лишь в положительной области переменной
выполнялся
лишь в положительной области переменной
 ,
либо в положительной области
,
либо в положительной области
 (частотной
области). Поскольку спектры периодических
сигналов существуют только в (
(частотной
области). Поскольку спектры периодических
сигналов существуют только в ( )
)
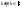 ,
то указанные спектры являются
дискретными. Следует отметить, что
из выражения ряда Фурье в sin-cos-форме
следует свойства: 1)
,
то указанные спектры являются
дискретными. Следует отметить, что
из выражения ряда Фурье в sin-cos-форме
следует свойства: 1)
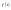 -
четная функция может быть описана
рядом Фурье лишь
-
четная функция может быть описана
рядом Фурье лишь
 (
(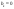 )
; 2)
)
; 2)
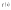 - нечсетная функция может быть описана
рядом Фурье
- нечсетная функция может быть описана
рядом Фурье
 .
На практике для построения спектров
периодического сигнала используют
cos-форму
ряда Фурье:
.
На практике для построения спектров
периодического сигнала используют
cos-форму
ряда Фурье:
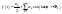 (1).
Выражение (1) называется гармоникой,
если работа ведется с сигналами вида
напряжения и тока, то форма (1) имеет
вид:
(1).
Выражение (1) называется гармоникой,
если работа ведется с сигналами вида
напряжения и тока, то форма (1) имеет
вид:
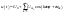 ,
где
,
где
 -
нулевая гармоника, а
-
нулевая гармоника, а
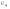 - амплитудное значение.
- амплитудное значение.
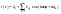 .
На практике ряд Фурье ограничивают с
учетом полосы пропускания цепи и
ширины спектра сигнала. В результате
выражение (1) – представление
периодического сигнала бесконечной
суммы его гармоник.
.
На практике ряд Фурье ограничивают с
учетом полосы пропускания цепи и
ширины спектра сигнала. В результате
выражение (1) – представление
периодического сигнала бесконечной
суммы его гармоник.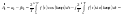
 Для
определенности рассмотрения перехода
к преобразованию Лапласа изменим
пределы интегрирования.
Для
определенности рассмотрения перехода
к преобразованию Лапласа изменим
пределы интегрирования.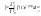 .
.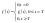
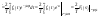 .
Т.о.:
.
Т.о.:
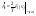 .
Согласно указанному выражению для
нахождения комплексного спектра
.
Согласно указанному выражению для
нахождения комплексного спектра
 периодического
сигнала
периодического
сигнала
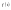 необходимо проделать следующие
операции: 1) в периодическом сигнале
выделить сигнал на первом периоде. 2)
найти изображение одиночного импульса.
3) Выполнить замену в виде равенства
необходимо проделать следующие
операции: 1) в периодическом сигнале
выделить сигнал на первом периоде. 2)
найти изображение одиночного импульса.
3) Выполнить замену в виде равенства
 ,
,
 и вычислить при различных комплексный
спектр.
и вычислить при различных комплексный
спектр.
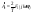 .
.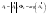
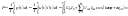
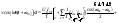
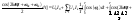
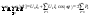 .
Вывод: Активная мощность в цепи при
периодических сигналах = сумме активных
мощностей, определяемых на каждой
гармонике. На основе аналогичных
выводов можно получить аналогичное
выражение для действующих значение
токов и напряжений, если эти сигналы
периодичны:
.
Вывод: Активная мощность в цепи при
периодических сигналах = сумме активных
мощностей, определяемых на каждой
гармонике. На основе аналогичных
выводов можно получить аналогичное
выражение для действующих значение
токов и напряжений, если эти сигналы
периодичны: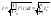 ,
,
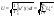 .
Отметим:
.
Отметим: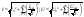
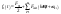 ,
где
,
где
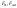 - амплитудный спектр воздействия, а
- амплитудный спектр воздействия, а
 -
фазовый. Чем больше
-
фазовый. Чем больше
 тем точнее восстанавливается входной
сигнал цепи. 2) определяются частотные
характеристики цепи
тем точнее восстанавливается входной
сигнал цепи. 2) определяются частотные
характеристики цепи
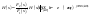 .
Вычисляются дискретные спектры и
формируется выходной сигнал цепи:
.
Вычисляются дискретные спектры и
формируется выходной сигнал цепи:
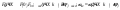 .
Результат:
.
Результат:
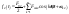
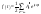 (1)
– комплексный вид.
(1)
– комплексный вид.
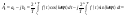
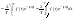 (2).
Подставим выражение (2) в выражение
(1).
(2).
Подставим выражение (2) в выражение
(1).
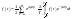 (3).
Перейдем от периодического сигнала
(3).
Перейдем от периодического сигнала
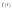 к
апериодическому сигналу, введя
предположение, что апериодический
сигнал это периодический сигнал с
к
апериодическому сигналу, введя
предположение, что апериодический
сигнал это периодический сигнал с
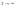 .
Из указанного условия следует:
.
Из указанного условия следует:
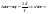 расстояние
м/у отсчетами дискретного спектра,
мал и в пределе дискретный сперт
превращается в непрерывную функцию.
расстояние
м/у отсчетами дискретного спектра,
мал и в пределе дискретный сперт
превращается в непрерывную функцию.
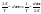 .
Сумма переходит в интерал:
.
Сумма переходит в интерал:
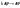 .
На основе указанного перехода
апериодически сигнал с использованием
выражения (3) модно представить в виде:
.
На основе указанного перехода
апериодически сигнал с использованием
выражения (3) модно представить в виде:
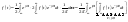 по
прямому преобразованию Фурье.
по
прямому преобразованию Фурье.
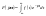 (4)
(4)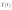 непериодическая,
обладающая свойствами:
непериодическая,
обладающая свойствами:
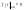 и
и
 тогда
односторонние преобразования Фурье
имеют вид:
тогда
односторонние преобразования Фурье
имеют вид:
 .
Сравним указанные формулы (1) и (2) с
формулами преобразования Лапласа:
.
Сравним указанные формулы (1) и (2) с
формулами преобразования Лапласа: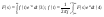 .
Из указанных равенств следует, что
формулы (3) и (4) тождественно равны (1)
и (2) при условии
.
Из указанных равенств следует, что
формулы (3) и (4) тождественно равны (1)
и (2) при условии
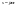 .
Следует отметить, что спектральное
представление, получаемое на основе
преобразования Фурье непериодических
сигналов, водится для качественного
анализа степени искажения входного
сигнала, проходящего через цепь.
.
Следует отметить, что спектральное
представление, получаемое на основе
преобразования Фурье непериодических
сигналов, водится для качественного
анализа степени искажения входного
сигнала, проходящего через цепь.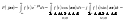
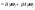 .
У четных сигналов
.
У четных сигналов
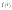 существует
лишь вещественный спектр (
существует
лишь вещественный спектр ( ).
У нечетных сигналов лишь мнимый спектр
(
).
У нечетных сигналов лишь мнимый спектр
( ).
Из указанных спектров формируется
).
Из указанных спектров формируется
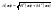 - амплитудный спектр.
- амплитудный спектр.
 - фазовый спектр. Спектры непериодических
сигналов являются непрерывными
функциями частоты:
- фазовый спектр. Спектры непериодических
сигналов являются непрерывными
функциями частоты:
 -
комплексный спектр. Спектры
непериодических сигналов в результате
формируется следующим образом:
-
комплексный спектр. Спектры
непериодических сигналов в результате
формируется следующим образом:
 .
.
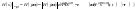 .
Таким образом частотные характеристики
цепи это фазовые и амплитудные сперты
импульсной характеристики
.
Таким образом частотные характеристики
цепи это фазовые и амплитудные сперты
импульсной характеристики
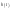 .
На основе спектрального спектра
запишем представление непериодического
сигнала.
.
На основе спектрального спектра
запишем представление непериодического
сигнала.
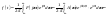
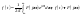 .
Таким образом периодический сигнал
удовлетворяющий условию Дирихле
представляется в виде ряда Фурье (
.
Таким образом периодический сигнал
удовлетворяющий условию Дирихле
представляется в виде ряда Фурье (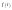 - непериодический, обладающий свойством:
- непериодический, обладающий свойством:
 (5))
могут быть описаны преобразованием
в ряд Фурье. (4) существуют при выполнении
условий (5).
(5))
могут быть описаны преобразованием
в ряд Фурье. (4) существуют при выполнении
условий (5).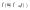 .
С характеристиками [
.
С характеристиками [ и
и
 ]
и [
]
и [ и
и
 ]
соответственно.
]
соответственно.
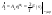 ;
;
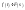 .
.
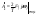 ,
где
,
где
 - комплексный спектр.
- комплексный спектр.
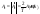 - амплитудный спектр;
- амплитудный спектр;
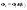 - фазовый спектр. Таким образом
амплитудный спектр непериодического
сигнала является огибающей с
коэффициентом
- фазовый спектр. Таким образом
амплитудный спектр непериодического
сигнала является огибающей с
коэффициентом
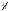 амплитудного спектра периодического
сигнала. Дискретный фазовый спектр
периодического сигнала формируется
путем дискретизации частотной области
амплитудного спектра периодического
сигнала. Дискретный фазовый спектр
периодического сигнала формируется
путем дискретизации частотной области
 из
фазового спектра одиночного сигнала.
из
фазового спектра одиночного сигнала.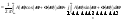 (1).
В симметричных пределах с нечетной
функцией sin
под знаком интеграла они стремятся к
0. Таким образом непериодических
сигнал формируется бесконечной суммой
гармонических составляющих амплитуды
которых образуют амплитудный спектр,
а начальные фазы – фазовые спектры.
Из выражения (1) следует, что реально
амплитудами гармоник являются
(1).
В симметричных пределах с нечетной
функцией sin
под знаком интеграла они стремятся к
0. Таким образом непериодических
сигнал формируется бесконечной суммой
гармонических составляющих амплитуды
которых образуют амплитудный спектр,
а начальные фазы – фазовые спектры.
Из выражения (1) следует, что реально
амплитудами гармоник являются
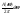 поэтому
в действительность амплитуды гармоник
характеризуются плотностью распределения
амплитудного спектра по частоте. В
результате точное название амплитудного
спектра это спектральная плотность
амплитуд указанных выше гармоник.
поэтому
в действительность амплитуды гармоник
характеризуются плотностью распределения
амплитудного спектра по частоте. В
результате точное название амплитудного
спектра это спектральная плотность
амплитуд указанных выше гармоник.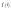 ,
для которого определим энергию:
,
для которого определим энергию:
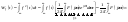
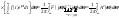 .
На основе полученной связи энергии
сигнала и его амплитудного спектра
формируется энергетический критерий
определения ширины спектра. Шириной
спектра называется
диапазон частот в районе
.
На основе полученной связи энергии
сигнала и его амплитудного спектра
формируется энергетический критерий
определения ширины спектра. Шириной
спектра называется
диапазон частот в районе
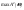 в
котором сосредоточенно
в
котором сосредоточенно
 энергии
сигнала (
энергии
сигнала ( ).
На практике для определения ширины
спектра используют амплитудный
критерий: Шириной
спектра называют
диапазон частот, в котором значения
амплитудного спектра удовлетворяют
условию:
).
На практике для определения ширины
спектра используют амплитудный
критерий: Шириной
спектра называют
диапазон частот, в котором значения
амплитудного спектра удовлетворяют
условию:
 .
В этом критерии в качестве может быть
5, 10. 5% амплитудный критерий соответствует
95% энергетическому, а 10% - 99%. Таким
образом ширина спектра – определяется
графически.
.
В этом критерии в качестве может быть
5, 10. 5% амплитудный критерий соответствует
95% энергетическому, а 10% - 99%. Таким
образом ширина спектра – определяется
графически.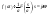 .
Если длительность сигнала изменить
в несколько раз (
.
Если длительность сигнала изменить
в несколько раз (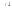 ),
то в столько раз измениться его спектр
(
),
то в столько раз измениться его спектр
(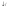 ).
Чем короче сигнал тем шире его спектр.
).
Чем короче сигнал тем шире его спектр.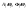 - известно (апериодический сигнал).
Найти
- известно (апериодический сигнал).
Найти
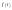 .
. .
Полученные дискретные спектры
подставляют в ряд Фурье в cos-форме
и получаем периодический сигнал.
Сигнал на периоде обладает заданными
спектрами.
.
Полученные дискретные спектры
подставляют в ряд Фурье в cos-форме
и получаем периодический сигнал.
Сигнал на периоде обладает заданными
спектрами.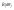 ,
либо мнимый
,
либо мнимый
 спектр.
Восстановить сам сигнал. Пусть
спектр.
Восстановить сам сигнал. Пусть
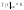 .
Для его представления используем
обратное преобразование Фурье.
.
Для его представления используем
обратное преобразование Фурье.
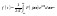
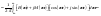
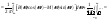
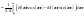 (1).
Рассмотрим сигнал
(1).
Рассмотрим сигнал
 (2).
Из выражения (1) вычитаем выражение
(2)
(2).
Из выражения (1) вычитаем выражение
(2)
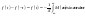 (3).
Суммируем (1) и (2):
(3).
Суммируем (1) и (2):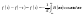 (4)
(4) - нечетная функция
- нечетная функция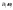 -
четная функция. На основе данного
свойства выражения (3) и (4) под интегралом
имеют четные функции. В результате
вводится преобразование:
-
четная функция. На основе данного
свойства выражения (3) и (4) под интегралом
имеют четные функции. В результате
вводится преобразование: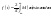 и
и