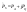-
Электрический
ток, напряжение…
Электрическим
током
называется упорядоченное движение
частиц - носителей тока. Постоянный
ток
– ток неизменимый во времени.
Электрический ток характеризуется
силой
тока.
 ,
где ,
где
 -
величина заряда, т.е. -
величина заряда, т.е.
 .
Помимо величины существует и направление
тока, связанное с перемещением
положительных зарядов (если I
= 2A,
то имеются ввиду положит заряды; I=-2A
– отрицательные). Направления токов
выбираются произвольно. .
Помимо величины существует и направление
тока, связанное с перемещением
положительных зарядов (если I
= 2A,
то имеются ввиду положит заряды; I=-2A
– отрицательные). Направления токов
выбираются произвольно.
 При
перемещении зарядов в цепи выделяется
или потребляется энергия.
При
перемещении зарядов в цепи выделяется
или потребляется энергия.
 .
При расчете цепей рекомендуется
выбирать согласованное включение
элементов цепи. .
При расчете цепей рекомендуется
выбирать согласованное включение
элементов цепи.
При
перемещении элементарного заряда
выделяется следующая энергия:
 (1).
Мощность
– скорость
потребления энергии элементом: (1).
Мощность
– скорость
потребления энергии элементом:
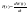 (2).
Из
(1)и(2) => (2).
Из
(1)и(2) =>
 .
Из (2): .
Из (2):
 .
Элемент называется
пассивным, если
в любой момент времени их энергия
положительна, т.е. .
Элемент называется
пассивным, если
в любой момент времени их энергия
положительна, т.е.
 .
Если на элементе его мощность >0, то
элемент потребляет энергию, в противном
случае – отдает. .
Если на элементе его мощность >0, то
элемент потребляет энергию, в противном
случае – отдает.
|
-
Резистивный
элемент.
Резистивный
элемент характеризуется своим
сопротивлением.
 ,
где ,
где
 -
удельное сопротивление, зависящая
от свойств материала. Закон Ома для
R-элемента: -
удельное сопротивление, зависящая
от свойств материала. Закон Ома для
R-элемента:
 .
ВАХ R-элемента
( .
ВАХ R-элемента
( ) )
G
– проводимость =
 [Сим].
Мощность на R-элементе [Сим].
Мощность на R-элементе
 .
R-элемент
всегда потребляет энегию, т.к. .
R-элемент
всегда потребляет энегию, т.к.
 (ВСЕГДА). (ВСЕГДА).
 =>
R-элемент
– пассивен. =>
R-элемент
– пассивен.
|
-
Источники
электромагнитной энергии. Идеальные
источники…
Реальные
источники электрической энергии
имеет ЭДС
 и внутреннее сопротивление
и внутреннее сопротивление
 .
Тогда сопротивление на его зажимах: .
Тогда сопротивление на его зажимах:
 .
Если по этому источнику будет протекать
ток i,
то напряжение будет убывать. .
Если по этому источнику будет протекать
ток i,
то напряжение будет убывать.
 .
Рассмотрим два предельных случая: .
Рассмотрим два предельных случая:
1.
 ,
т.е. напряжение не зависит от протекающего
через него тока ( ,
т.е. напряжение не зависит от протекающего
через него тока ( =0).
Такой источник называется источником
напряжения. =0).
Такой источник называется источником
напряжения.
2.
Пусть
 и
и
 ,
тогда ,
тогда
 и
мы получим, что и
мы получим, что
 ,
где а – некоторое число. Такой источник
называется источником
тока. ,
где а – некоторое число. Такой источник
называется источником
тока.
|
9.
Эквивалентное преобразование
источников.
|
|
11.
МКТ.
Порядок
расчета:
1.
Выбрать направления и задать номера
контурных токов. Если есть ИТ, то номер
контурного тока, проходящего через
ИТ, рекомендуется задавать последним.
Через ИТ должен проходить только один
контурный ток!
2.
Составить систему независимых
уравнений:
 . .
 ,
где ,
где
 -
собственное сопротивление i-того
контура, а -
собственное сопротивление i-того
контура, а
 -
взаимное сопротивление i-того
и j-того
контуров («+», если -
взаимное сопротивление i-того
и j-того
контуров («+», если
 и и
 сонаправлены и «-» - в противном случае)
сонаправлены и «-» - в противном случае)
 -
сумма источников напряжений, относящихся
у i-тому
узлу (если по направлению обхода «-»,
то «+», в противном случае – «-»). -
сумма источников напряжений, относящихся
у i-тому
узлу (если по направлению обхода «-»,
то «+», в противном случае – «-»).
3.
Решить систему и определить напряжения
(токи) цепи.
 . .
|
12.
МУН.
Порядок
расчета:
1.
Преобразовать ИН в ИТ (если возможно)
2.
Расставить узлы преобразованной цепи
(каждому узлу соответствует его
 ),
один из узлов принять базисным (его
потенциал =0). Если остались ИН, то его
«-» задает положение базисного узла,
а «+» - узел, номер которого рекомендуется
задавать последним. ),
один из узлов принять базисным (его
потенциал =0). Если остались ИН, то его
«-» задает положение базисного узла,
а «+» - узел, номер которого рекомендуется
задавать последним.
3.
Составить систему независимых
уравнений:
 . .
 ,
где ,
где
 -
собственная проводимость i-того
узла, а -
собственная проводимость i-того
узла, а
 -
взаимная проводимость i-того
и j-того
узлов (всегда «-»). -
взаимная проводимость i-того
и j-того
узлов (всегда «-»).
 -
сумма источников токов, относящихся
у i-тому
узлу (исход – «-», а вход – «+»). -
сумма источников токов, относящихся
у i-тому
узлу (исход – «-», а вход – «+»).
4.
Решить систему и определить напряжения
(токи) цепи.
 . .
5.
Вернуться к исходной цепи.
|
13.
Метод
эквивалентного источника напряжения.
|
14.
Метод эквивалентного источника тока.
|
|
15.
L-элемент
цепи. Основная х-ка, ВАХ, закон
коммутации.
L-элемент
– двухполюсник, характеризующий одну
из сторон ЭМ-процесса, а именно
накопление энергии магнитного поля.
Основная х-ка – индуктивность.
 ,
где ,
где
 -
потокосцепление, т.е. индуктивность
– отношение потокосцепления к току
его вызвавшему. L
характеризуется вебер-амперной
характеристикой. -
потокосцепление, т.е. индуктивность
– отношение потокосцепления к току
его вызвавшему. L
характеризуется вебер-амперной
характеристикой.
 .
Построим ВАХ L: .
Построим ВАХ L:
 . .
Следовательно:
1.
 2.
если нам изве- 2.
если нам изве-
стен
ток на L
к моменту времени
 ,
то ,
то
 3.
Если
в цепи постоянное воздействие, то 3.
Если
в цепи постоянное воздействие, то
 ,
т.к. ,
т.к.
 .
При постоянном воздействии тока L
заменятся
на к.з. Энергия L: .
При постоянном воздействии тока L
заменятся
на к.з. Энергия L:
 .
Если .
Если
 ,
то ,
то
 и
L
накапливает энергию МП, в противном
случае – отдает энергию в цепь.
Энергия: и
L
накапливает энергию МП, в противном
случае – отдает энергию в цепь.
Энергия:

 ,
поскольку ,
поскольку
 ,
то ,
то
 и
следовательно L
– пассивен,
т.е. потребляет энергию. Закон
коммутации: и
следовательно L
– пассивен,
т.е. потребляет энергию. Закон
коммутации:
 при при
 -
конечном, т.е. -
конечном, т.е.
 .
Док-во:
допустим
противоположное: .
Док-во:
допустим
противоположное:
 ,
т.е. ,
т.е.
 ,
а это противоречит условию. Вывод: ,
а это противоречит условию. Вывод:
|
16.
С-элемент. Основная х-ка, ВАХ, закон
коммутации.
С-элемент
– такой
двухполюсник, который характеризует
одну из сторон ЭМ-процесса, а именно
запасание энергии ЭП. Основная х-ка
– емкость:
 .
С
характеризуется
кулон-вольтовой характерис- .
С
характеризуется
кулон-вольтовой характерис-
тикой.
Построим ВАХ элемента
 .
Следствия: .
Следствия:
1.

2.
Если в цепи известно напряжение на С
к
моменту
 ,
то ,
то
3.
При постоянном воздействии
 ,
т.е. С
эквивалентен
обрыву (х.х.). Энергия С ,
т.е. С
эквивалентен
обрыву (х.х.). Энергия С
 и
и

 ,
т.е. W
– всегда положительна ,
т.е. W
– всегда положительна
 С
– пассивен.
Закон
коммутации: При С
– пассивен.
Закон
коммутации: При
 -
конечном -
конечном
 ,
т.е. ,
т.е.

|
19.
Любой
выходной сигнал динамической цепи
1ого
порядка
при коммутации имеет вид:
 (1)
(1)
Алгоритм:
1.
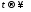 (вынужденный режим) в данном режиме
L=к.з.,
С=х.х. Определяем
(вынужденный режим) в данном режиме
L=к.з.,
С=х.х. Определяем
 ( в режиме посткоммутации (t>0))
( в режиме посткоммутации (t>0))
2.
 (до
коммутации) Если в цепи нет дополнительных
условий (нулевые начальные) в данном
режиме всегда находят начальные
условия цепи: (до
коммутации) Если в цепи нет дополнительных
условий (нулевые начальные) в данном
режиме всегда находят начальные
условия цепи:
 (одно из двух)
(одно из двух)
3.
 (сразу после коммутации) На основе
законов коммутации
(сразу после коммутации) На основе
законов коммутации
 с=И.Н.
с величиной с=И.Н.
с величиной
 , ,
 L=И.Т.
с величиной L=И.Т.
с величиной
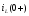 .
В полученной цепи находим реакцию .
В полученной цепи находим реакцию

4.
Определяем постоянную времени (в
режиме после коммутации): (в
режиме после коммутации):
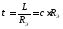 . .
 - сопротивление в режиме после
коммутации при исключенных источниках
относительно L/C-элементов.
- сопротивление в режиме после
коммутации при исключенных источниках
относительно L/C-элементов.
5.
Находим постоянную А:

6.
Ответ: имеет вид выражение (1), содержащее
полученные в результате расчетов
значения.
Расчет
переходных процессов в разветвленной
цепи RL/C.
|
20.
Процессы в последовательной RLC
при подключении к источнику const
U.
Апериодический, граничный и режим
затухающих колебаний.
|
|
21.
Определение порядка цепи. Особенности
коммутации в цепях при наличии
емкостных контуров и индуктивных
сечений.
Порядок
цепи
– это максимальная степень
дифференциального уравнения. Во
многих случаях порядок равен
накопительных элементов ( ),
однако если цепь содержит Cконтуры
или
Lсечения
(узлы, у которых примыкающие ветви
содержат L),
то порядок цепи снижается. ),
однако если цепь содержит Cконтуры
или
Lсечения
(узлы, у которых примыкающие ветви
содержат L),
то порядок цепи снижается.
|
23.
Единичная ступенчатая, единичная
импульсная и функция единичного
наклона. Связь м/у ними. Применение в
ТОЭ.
Некоторые
стандартные сигналы, на которые
необходимо находить отклики (из них
можно выразить все остальные).
-
Единично-ступенчатая
функция (f
Харисайда):
 или или

Используется
для выделения функции в некотором
времени.
-
Единичная
импульсная функция (f
Диракле, сингулярная f)
 .
Свойства: .
Свойства:
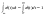 , ,
т.о.

-
Функция
единичного наклона
 ,
очевидно, что: ,
очевидно, что:

|
24.
Переходная характеристика цепи.
Импульсная характеристика. Характеристика
 . .
Переходная
характеристика
 численно равна реакции цепи при
нулевых ННУ на единственное в цепи
воздействие вида единичной ступенчатой
функции
численно равна реакции цепи при
нулевых ННУ на единственное в цепи
воздействие вида единичной ступенчатой
функции
 . .
 ,
где ,
где -
обычная непрерывная функция, у которой: -
обычная непрерывная функция, у которой:
 . .
Импульсная
характеристика:
 численно
равна реакции при нулевых ННУ на
единственное в цепи воздействие вида
единичной импульсной функции численно
равна реакции при нулевых ННУ на
единственное в цепи воздействие вида
единичной импульсной функции
 . .
 .
Поскольку .
Поскольку
 ,
то реакции связаны аналогично: ,
то реакции связаны аналогично:
 . .
Характеристика
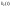 (весовая
характеристика):
численно равна реакции на воздействие
вида (весовая
характеристика):
численно равна реакции на воздействие
вида
 ;
может
быть найдена интегрированием ;
может
быть найдена интегрированием
 . .
|
26.
Интеграл наложения через импульсную
характеристику.
Пусть
 при при
 .
Разбиваем .
Разбиваем
 на
участки ширины на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию ,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав .
Просуммировав
реакции,
получим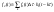 ,
если ,
если
 тогда
имеем тогда
имеем
 ,
если ,
если
 ,
то ,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 , ,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем: -функцию.
В итоге имеем:
Интеграл
Дюамеля:

|
|
26.
Интеграл наложения через импульсную
характеристику.
Пусть
 при при
 .
Разбиваем .
Разбиваем
 на
участки ширины на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию ,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав .
Просуммировав
реакции,
получим ,
если ,
если
 тогда
имеем тогда
имеем
 ,
если ,
если
 ,
то ,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 , ,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем: -функцию.
В итоге имеем:
Интеграл
свертки:

|
26.
Интеграл наложения через импульсную
характеристику.
Пусть
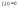 при при
 .
Разбиваем .
Разбиваем
 на
участки ширины на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию ,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав .
Просуммировав
реакции,
получим ,
если ,
если
 тогда
имеем тогда
имеем
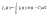 ,
если ,
если
 ,
то ,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 , ,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем: -функцию.
В итоге имеем:
Интеграл
свертки:

Интеграл
Дюамеля:

|
27.
Среднее и действующие значение
гармонической функции.
Среднее
за период T
значение
определяется как
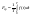 ,
если ,
если
 -
гармоническое, то -
гармоническое, то
 .
Средневыпрямленное значение – среднее
значение положительной полуволны. .
Средневыпрямленное значение – среднее
значение положительной полуволны.
 .
Действительное
значение периодического тока
– такое значение постоянного тока,
которое за время, равное периоду,
выделит в R
равное количество энергии. В общем
случае: .
Действительное
значение периодического тока
– такое значение постоянного тока,
которое за время, равное периоду,
выделит в R
равное количество энергии. В общем
случае:
 ,
если ,
если
 ,
то ,
то

|
30.
Закон Ома и Кирхгофа в комплексной
форме.
Формы
записи комплексного числа:
 , , -
сопряженное. Сумма -
сопряженное. Сумма
 : : ,
если ,
если
 ,то ,то
 ,
т.е. ,
т.е.

Закон
токов Кирхгофа:
 ,
тогда ,
тогда

Закон
напряжения Кирхгофа:
Проводя
аналогичные рассуждения
 .
Введем понятие комплексного R: .
Введем понятие комплексного R:
 ,
где ,
где
 -
активное, а -
активное, а
 -
реактивное сопротивления. -
реактивное сопротивления.
Закон
Ома в комплексной форме:

|
|
31.
R-эл-т
в синусоидальном режиме.
По
закону Ома:
 . .
Теперь
подставим
 получим
получим
 . .
Теперь
напишем для комплексного сопротивления:
 . .
Комплексная
проводимость:
 . .

|
32.
L-эл-т
в синусоидальном режиме. (33. С-эл-т в
sin-режиме
– а.)
 ,
подставим синусоидальные напряжение
и ток: ,
подставим синусоидальные напряжение
и ток:
 в
L: в
L:
 ,
т.е. фазовый сдвиг: ,
т.е. фазовый сдвиг:
 ; ;
 -
индуктивное сопротивление.
-
индуктивное сопротивление.
 . .
Теперь
пусть
 .
Подставляя в ВАХ, получим: .
Подставляя в ВАХ, получим:
 или или .
Величина .
Величина
 -
комплексное сопротивление. -
комплексное сопротивление.
|
34.
Мощность в синусоидальном режиме.
Пусть
через элемент течет ток
 и
и
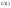 , ,
 . .
 -
мгновенная мощность: -
мгновенная мощность:
  . .
Активная
мощность:
 ,
где ,
где

Реактивная
мощность:
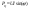 . .
Активная
мощность зависит от
 .
При .
При
  -
полная мощность. -
полная мощность.
|
35.
Мощность в комплексной форме.
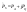
|


 ,
где
,
где
 -
величина заряда, т.е.
-
величина заряда, т.е.
 .
Помимо величины существует и направление
тока, связанное с перемещением
положительных зарядов (если I
= 2A,
то имеются ввиду положит заряды; I=-2A
– отрицательные). Направления токов
выбираются произвольно.
.
Помимо величины существует и направление
тока, связанное с перемещением
положительных зарядов (если I
= 2A,
то имеются ввиду положит заряды; I=-2A
– отрицательные). Направления токов
выбираются произвольно. При
перемещении зарядов в цепи выделяется
или потребляется энергия.
При
перемещении зарядов в цепи выделяется
или потребляется энергия.
 .
При расчете цепей рекомендуется
выбирать согласованное включение
элементов цепи.
.
При расчете цепей рекомендуется
выбирать согласованное включение
элементов цепи. (1).
Мощность
– скорость
потребления энергии элементом:
(1).
Мощность
– скорость
потребления энергии элементом:
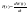 (2).
Из
(1)и(2) =>
(2).
Из
(1)и(2) =>
 .
Из (2):
.
Из (2): .
Элемент называется
пассивным, если
в любой момент времени их энергия
положительна, т.е.
.
Элемент называется
пассивным, если
в любой момент времени их энергия
положительна, т.е.
 .
Если на элементе его мощность >0, то
элемент потребляет энергию, в противном
случае – отдает.
.
Если на элементе его мощность >0, то
элемент потребляет энергию, в противном
случае – отдает. ,
где
,
где
 -
удельное сопротивление, зависящая
от свойств материала. Закон Ома для
R-элемента:
-
удельное сопротивление, зависящая
от свойств материала. Закон Ома для
R-элемента:
 .
ВАХ R-элемента
(
.
ВАХ R-элемента
( )
) [Сим].
Мощность на R-элементе
[Сим].
Мощность на R-элементе .
R-элемент
всегда потребляет энегию, т.к.
.
R-элемент
всегда потребляет энегию, т.к.
 (ВСЕГДА).
(ВСЕГДА).
 =>
R-элемент
– пассивен.
=>
R-элемент
– пассивен. и внутреннее сопротивление
и внутреннее сопротивление
 .
Тогда сопротивление на его зажимах:
.
Тогда сопротивление на его зажимах:
 .
Если по этому источнику будет протекать
ток i,
то напряжение будет убывать.
.
Если по этому источнику будет протекать
ток i,
то напряжение будет убывать. .
Рассмотрим два предельных случая:
.
Рассмотрим два предельных случая: ,
т.е. напряжение не зависит от протекающего
через него тока (
,
т.е. напряжение не зависит от протекающего
через него тока ( =0).
Такой источник называется источником
напряжения.
=0).
Такой источник называется источником
напряжения. и
и
 ,
тогда
,
тогда
 и
мы получим, что
и
мы получим, что
 ,
где а – некоторое число. Такой источник
называется источником
тока.
,
где а – некоторое число. Такой источник
называется источником
тока. .
. ,
где
,
где
 -
собственное сопротивление i-того
контура, а
-
собственное сопротивление i-того
контура, а
 -
взаимное сопротивление i-того
и j-того
контуров («+», если
-
взаимное сопротивление i-того
и j-того
контуров («+», если
 и
и
 сонаправлены и «-» - в противном случае)
сонаправлены и «-» - в противном случае) -
сумма источников напряжений, относящихся
у i-тому
узлу (если по направлению обхода «-»,
то «+», в противном случае – «-»).
-
сумма источников напряжений, относящихся
у i-тому
узлу (если по направлению обхода «-»,
то «+», в противном случае – «-»). .
. ),
один из узлов принять базисным (его
потенциал =0). Если остались ИН, то его
«-» задает положение базисного узла,
а «+» - узел, номер которого рекомендуется
задавать последним.
),
один из узлов принять базисным (его
потенциал =0). Если остались ИН, то его
«-» задает положение базисного узла,
а «+» - узел, номер которого рекомендуется
задавать последним. .
. ,
где
,
где
 -
собственная проводимость i-того
узла, а
-
собственная проводимость i-того
узла, а
 -
взаимная проводимость i-того
и j-того
узлов (всегда «-»).
-
взаимная проводимость i-того
и j-того
узлов (всегда «-»). -
сумма источников токов, относящихся
у i-тому
узлу (исход – «-», а вход – «+»).
-
сумма источников токов, относящихся
у i-тому
узлу (исход – «-», а вход – «+»). .
. ,
где
,
где
 -
потокосцепление, т.е. индуктивность
– отношение потокосцепления к току
его вызвавшему. L
характеризуется вебер-амперной
характеристикой.
-
потокосцепление, т.е. индуктивность
– отношение потокосцепления к току
его вызвавшему. L
характеризуется вебер-амперной
характеристикой. .
Построим ВАХ L:
.
Построим ВАХ L:
 .
. 2.
если нам изве-
2.
если нам изве- ,
то
,
то
 3.
Если
в цепи постоянное воздействие, то
3.
Если
в цепи постоянное воздействие, то
 ,
т.к.
,
т.к.
 .
При постоянном воздействии тока L
заменятся
на к.з. Энергия L:
.
При постоянном воздействии тока L
заменятся
на к.з. Энергия L:
 .
Если
.
Если
 ,
то
,
то
 и
L
накапливает энергию МП, в противном
случае – отдает энергию в цепь.
Энергия:
и
L
накапливает энергию МП, в противном
случае – отдает энергию в цепь.
Энергия:

 ,
поскольку
,
поскольку
 ,
то
,
то
 и
следовательно L
– пассивен,
т.е. потребляет энергию. Закон
коммутации:
и
следовательно L
– пассивен,
т.е. потребляет энергию. Закон
коммутации:
 при
при
 -
конечном, т.е.
-
конечном, т.е.
 .
Док-во:
допустим
противоположное:
.
Док-во:
допустим
противоположное:
 ,
т.е.
,
т.е.
 ,
а это противоречит условию. Вывод:
,
а это противоречит условию. Вывод: .
С
характеризуется
кулон-вольтовой характерис-
.
С
характеризуется
кулон-вольтовой характерис- .
Следствия:
.
Следствия:
 ,
то
,
то
 ,
т.е. С
эквивалентен
обрыву (х.х.). Энергия С
,
т.е. С
эквивалентен
обрыву (х.х.). Энергия С
 и
и

 ,
т.е. W
– всегда положительна
,
т.е. W
– всегда положительна
 С
– пассивен.
Закон
коммутации: При
С
– пассивен.
Закон
коммутации: При
 -
конечном
-
конечном
 ,
т.е.
,
т.е.


 ),
однако если цепь содержит Cконтуры
или
Lсечения
(узлы, у которых примыкающие ветви
содержат L),
то порядок цепи снижается.
),
однако если цепь содержит Cконтуры
или
Lсечения
(узлы, у которых примыкающие ветви
содержат L),
то порядок цепи снижается. или
или

 .
Свойства:
.
Свойства:
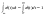 ,
,
 ,
очевидно, что:
,
очевидно, что:

 .
. численно равна реакции цепи при
нулевых ННУ на единственное в цепи
воздействие вида единичной ступенчатой
функции
численно равна реакции цепи при
нулевых ННУ на единственное в цепи
воздействие вида единичной ступенчатой
функции
 .
.
 ,
где
,
где -
обычная непрерывная функция, у которой:
-
обычная непрерывная функция, у которой:
 .
. численно
равна реакции при нулевых ННУ на
единственное в цепи воздействие вида
единичной импульсной функции
численно
равна реакции при нулевых ННУ на
единственное в цепи воздействие вида
единичной импульсной функции
 .
.
 .
Поскольку
.
Поскольку
 ,
то реакции связаны аналогично:
,
то реакции связаны аналогично:
 .
.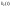 (весовая
характеристика):
численно равна реакции на воздействие
вида
(весовая
характеристика):
численно равна реакции на воздействие
вида
 ;
может
быть найдена интегрированием
;
может
быть найдена интегрированием
 .
.
 при
при
 .
Разбиваем
.
Разбиваем
 на
участки ширины
на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию
,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав
.
Просуммировав
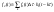 ,
если
,
если
 тогда
имеем
тогда
имеем
 ,
если
,
если
 ,
то
,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 ,
,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем:
-функцию.
В итоге имеем:

 при
при
 .
Разбиваем
.
Разбиваем
 на
участки ширины
на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию
,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав
.
Просуммировав
 ,
если
,
если
 тогда
имеем
тогда
имеем
 ,
если
,
если
 ,
то
,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 ,
,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем:
-функцию.
В итоге имеем:

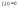 при
при
 .
Разбиваем
.
Разбиваем
 на
участки ширины
на
участки ширины
 ,
т.о. каждый кусочек будет иметь реакцию
,
т.о. каждый кусочек будет иметь реакцию
 .
Просуммировав
.
Просуммировав
 ,
если
,
если
 тогда
имеем
тогда
имеем
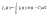 ,
если
,
если
 ,
то
,
то
 содержит импульсную функцию. В таком
случае:
содержит импульсную функцию. В таком
случае:
 ,
,
 - часть импульсной характеристики не
содержащая
- часть импульсной характеристики не
содержащая
 -функцию.
В итоге имеем:
-функцию.
В итоге имеем:


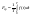 ,
если
,
если
 -
гармоническое, то
-
гармоническое, то
 .
Средневыпрямленное значение – среднее
значение положительной полуволны.
.
Средневыпрямленное значение – среднее
значение положительной полуволны.
 .
Действительное
значение периодического тока
– такое значение постоянного тока,
которое за время, равное периоду,
выделит в R
равное количество энергии. В общем
случае:
.
Действительное
значение периодического тока
– такое значение постоянного тока,
которое за время, равное периоду,
выделит в R
равное количество энергии. В общем
случае:
 ,
если
,
если
 ,
то
,
то

 ,
, -
сопряженное. Сумма
-
сопряженное. Сумма
 :
: ,
если
,
если
 ,то
,то
 ,
т.е.
,
т.е.

 ,
тогда
,
тогда

 .
Введем понятие комплексного R:
.
Введем понятие комплексного R:
 ,
где
,
где
 -
активное, а
-
активное, а
 -
реактивное сопротивления.
-
реактивное сопротивления.
 .
. получим
получим
 .
.
 .
. .
.

 ,
подставим синусоидальные напряжение
и ток:
,
подставим синусоидальные напряжение
и ток: в
L:
в
L:
 ,
т.е. фазовый сдвиг:
,
т.е. фазовый сдвиг:
 ;
; -
индуктивное сопротивление.
-
индуктивное сопротивление.
 .
. .
Подставляя в ВАХ, получим:
.
Подставляя в ВАХ, получим: или
или .
Величина
.
Величина
 -
комплексное сопротивление.
-
комплексное сопротивление. и
и
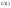 ,
,
 .
.
 -
мгновенная мощность:
-
мгновенная мощность:

 .
. ,
где
,
где

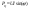 .
. .
При
.
При

 -
полная мощность.
-
полная мощность.