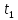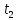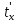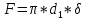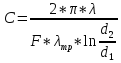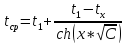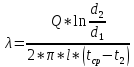Лабораторные / Лаба Термодинамика 1. Исследование теплопроводности неметаллических материалов

_{МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ}

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«Национальный исследовательский ядерный университет «МИФИ»

Озерский технологический институт –

филиал федерального государственного автономного образовательного учреждения высшего

образования «Национальный исследовательский ядерный университет «МИФИ»

(ОТИ НИЯУ МИФИ)

Кафедра ТМ и МАХП

Лабораторная работа №1

«Исследование теплопроводности

неметаллических материалов»

По дисциплине «Техническая термодинамика»

Принял				М.А. Миллер
Выполнил студент группы	1ТМ-36Д			П.С. Сергеев

Озёрск

2019

Цель работы: определение коэффициента теплопроводности твёрдых тел – плохих проводников тепла по методу трубы.

Приборы: установка.

Труба состоит из дюралюминиевой (марка Д16, 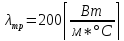) цилиндрической трубы 1 с толщиной стенки 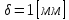, диаметром 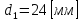и длиной 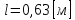, на которой закреплены элементы из исследуемого материала 2. Внутренний и наружный диаметры элементов составляют соответственно 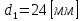и 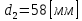. В качестве исследуемых материалов использованы: текстолит (труба № 1), асбоцемент (труба № 2) и гетинакс (труба № 3).

Внутри металлической трубы помещается электрический нагреватель 3 (нихромовая спираль), имеющий равномерное размещение витков по длине, что обеспечивает постоянную плотность теплового потока. Вся выделяющаяся тепловая мощность Q передается окружающей среде через боковую поверхность 2 и торцы 4. Нагреватель работает от источника питания 8. Мощность, потребляемая электрическим нагревателем, определяется по току в цепи нагревателя и падению напряжения на нём.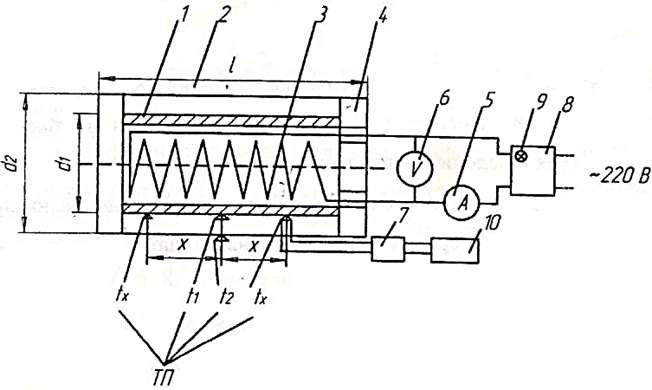

Для измерения силы тока в цепь последовательно включен амперметр 5, а для измерения напряжения на концах нагревателя – вольтметр 6.

Температура внутренней и наружной поверхностей исследуемого образца измеряется с помощью хромель-алюмелевых термопар. ЭДС термопар измеряется цифровым милливольтметром 10 через механический переключатель термопар 7.

Ход работы:

1. Включим установку и выведем её на стационарный режим.

2. Произведём измерение температур и снимем показания приборов 5 раз с интервалами в 2 минуты.

№ опыта					I, А		U, В
	ºC
1	136	58	88	115	1,4		90
2	140	60	90	118	1,4		88
3	145	61	92	125	1,4		87
4	147	62	94	128	1,4		87
5	150	64	97	133	1,4		88
Среднее	144	61	92	124	1,4		88

3. Произведём обработку результатов измерений.

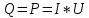– тепловой поток;

где:	F – площадь поперечного сечения металлической трубы, м2;
	d1 – наружный диаметр металлической трубы, м;
	δ – толщина стенки металлической трубы, м.

.

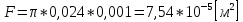где:	C – коэффициент, м-2;
	λ – искомый коэффициент теплопроводности изоляции, Вт/(м*ºC);
	λмт –коэффициент теплопроводности материала металлической трубы, Вт/(м*ºC);
	d1 – внутренний диаметр изоляции, м;
	d2 – наружный диаметр изоляции, м.

.

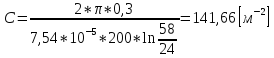где:	t1 – температура в середине трубы, ºC;
	tx – температура внутренней поверхности изоляции на расстоянии x метров от середины трубы (0,27 м).

;

;

;

;

.

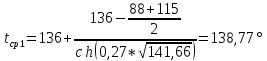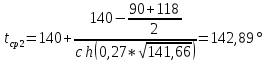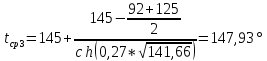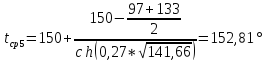где:	l – длина трубы;
	t2 – температура на внешней поверхности изоляции.

;

;

;

;

.

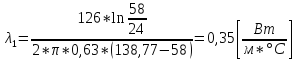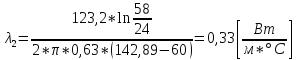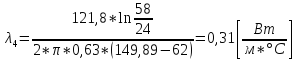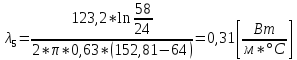Полученные значения коэффициентов теплопроводности оказались близки ожидаемым.

Контрольные вопросы:

1. Закон Фурье и его математическое описание. Градиент температуры.

Закон Фурье - вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры:

.

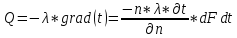где: λ – коэффициент теплопроводности, Вт/(м*К).

Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту. "-" – противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры. Коэффициент теплопроводности определяет плотность теплового потока при градиенте температуры 1 К/м.

2. Коэффициент теплопроводности, его физический смысл.

Коэффициент теплопроводности – количественная способность вещества проводить тепло. Равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1/К).

3. Распределение температуры в цилиндрической стенке. Тепловой поток через цилиндрическую стенку.

При стационарном процессе теплопроводности в цилиндрической однослойной стенке с внутренним радиусом r₁ и наружным r₂ уравнение распределения температуры имеет вид: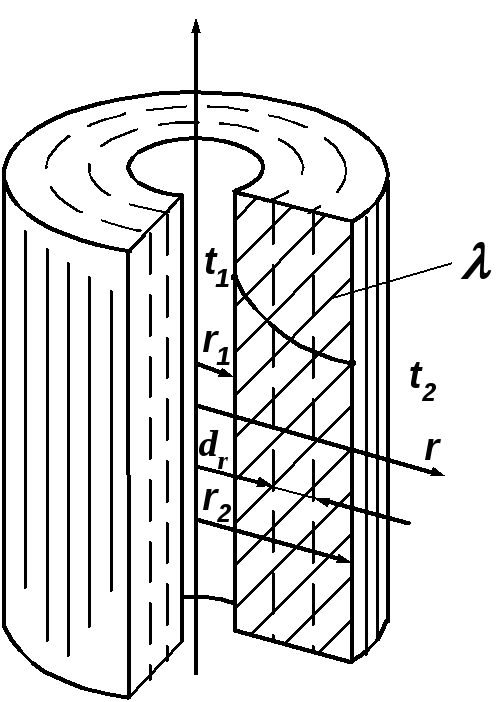

.

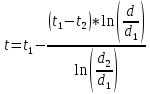Уравнение представляет собой уравнение логарифмической кривой. Распределение температуры в цилиндрической стенке является криволинейным. В случае плоской стенки плотность теплового потока остается одинаковой для всех изотермических поверхностей и градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность изменяется, т. к. величина поверхности зависит от радиуса (H=2*π*r*l), что приводит к изменению градиента температуры.

Из общего закона Фурье можно получить закон Фурье для цилиндрической стенки:

→ .
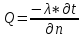
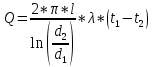