
- •Оглавление
- •Введение
- •Анализ уровня техники кориолисовых расходомеров
- •Постановка задачи
- •Принцип действия кориолисового раходомера
- •– Конструкция измерительных трубок расходомера
- •– Функциональная схема кориолисового расходомера
- •– Колебания измерительной трубки в кориолисовом расходомере
- •– Направление силы кориолиса в трубке
- •– Изгиб трубки под действием силы Кориолиса
- •– Связь угла закручивания с временной задержкой
- •Измерение расхода при двухфазном потоке
- •– Рост погрешности измерения расхода при увеличении содержания воздуха для малых и средних массовых расходов
- •– Рост погрешности измерения расхода при увеличении содержания воздуха для больших массовых расходов
- •– Эффект «расщепления фаз» и смещения центра масс
- •Обработка измерительных сигналов в кориолисовом расходомере
- •Исходные данные для исследования
- •Модель сигналов кориолисова расходомера
- •– Вид модельных сигналов с измерительных катушек
- •– Изменение параметров модельных сигналов с течением времени
- •Описание эксперимента по проливке кориолисова расходомера
- •– Схема проливочного стенда
- •– Вид измерительных сигналов при высоком gvf
- •– Зависимость числа ложных переходов от gvf
- •– Восстановление точного значения времени перехода через ноль
- •– Ложные переходы в левом измерительном сигнале
- •– Анализ расположения ложных переходов в измерительных сигналах
- •– Блок-схема модифицированного алгоритма переходов через ноль
- •Разработка предварительного фильтра
- •Общие сведения о цифровых фильтрах
- •Формирование требований к фильтру
- •– Пример задания требований к частотной характеристике а) для фнч; б) для пф
- •– Спектры измерительных сигналов расходомера а) – спектры сигналов при расходе 0,3 кг/с, б) при расходе 0,8 кг/с.
- •– Изменение частоты колебаний трубок для расхода 0,8 кг/с
- •Сглаживающие фильтры:
- •Некаузальные фильтры:
- •Каузальные фильтры
- •– Частотная характеристика оптимального ких-фильтра нижних частот
- •– Подбор параметров оптимального ких-фильтра с линейной фазой
- •– Сравнение частотных характеристик ких-фильтров с различными параметрами
- •– Импульсная характеристика и диаграмма нулей/полюсов для оптимального линейно-фазового ких-фильтра
- •– Подбор параметров минимально-фазового ких-фильтра
- •– Сравнение частотных характеристик минимально-фазовых ких-фильтров
- •– Диаграмма для оценки порядка эллиптического фильтра
- •– Подбор параметров эллиптического бих-фильтра
- •– Сравнение частотных характеристик бих-фильтров
- •Сглаживающие фильтры
- •– Сравнение внешнего вида сигналов на выходе различных типов фильтров
- •– Типовая схема средства измерений
- •– Деформация функции измерения расходомера с ростом gvf
- •Разработка параметрической модели для расчета расхода в условиях двухфазного потока
- •– Зависимость
- •– Зависимость
- •– Зависимость
- •Проверка модели для расчета расхода на реальном сигнале
- •– Погрешность расчета по базовой линейной модели (модель 0)
- •– Погрешность расчета по линейной модели с зависимыми от gvf коэффициентами (модель 1)
- •– Погрешность расчета расхода по линейным моделям с коррекцией
- •– Погрешность расчета расхода по квадратичным моделям с коррекцией
- •Заключение библиографический список
-
– Сравнение частотных характеристик минимально-фазовых ких-фильтров
(дополнить)
Таким образом, получены два КИХ фильтра для дальнейшего сравнения, коэффициенты фильтров приведены в приложении .
Фильтр с бесконечной импульсной характеристикой (БИХ-фильтр).
Выходной сигнал БИХ-фильтра ( зависит только как от входного сигнала
зависит только как от входного сигнала
 ,
так и от предыдущих отсчетов выходного
сигнала (фильтр является рекурсивным)
и описывается соотношением:
,
так и от предыдущих отсчетов выходного
сигнала (фильтр является рекурсивным)
и описывается соотношением:

где
 – импульсная характеристика фильтра;
– импульсная характеристика фильтра;
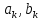 – коэффициенты фильтра;
– коэффициенты фильтра;
 – порядок числителя системной функции
фильтра;
– порядок числителя системной функции
фильтра;
 – порядок знаменателя системной функции
фильтра.
– порядок знаменателя системной функции
фильтра.
Основные свойства БИХ-фильтров:
-
устойчивость не гарантируется;
-
нелинейность ФЧХ;
-
чувствительность к шуму округления и ошибкам квантования;
-
обеспечение требуемых частотных характеристик при малом порядке фильтра (по сравнению с КИХ-фильтрами)
-
малое количество вычислительных операций (сложение и умножение).
Цель синтеза БИХ фильтра – определение
значений коэфициентов
 ,
которые удовлетворяют спецификациям
фильтра. Выделяют 4 способа синтеза
БИХ-фильтров.
,
которые удовлетворяют спецификациям
фильтра. Выделяют 4 способа синтеза
БИХ-фильтров.
-
Метод размещения нулей и полюсов. Размещение нулей и полюсов вручную позволяет быстро получать требуемый вид частотных характеристик для фильтров малых порядков. Однако, с возрастание порядка фильтра, применение данного способа становится нецелесообразным.
-
Метод инвариантного преобразования импульсной характеристики. Суть метода состоит в получении непрерывной импульсной характеристики желаемого вида с последующей ее дискретизацией. Метод требует высокой частоты дискретизации, не применим для синтеза ФВЧ и режекторных фильтров.
-
Согласованное
 -преобразование.
Суть метода состоит в переходе от
аналоговой передаточной функции фильтра
к цифровой на основании отражения нулей
и полюсов. Метод имеет схожие ограничения
с методом инвариантного преобразования
импульсной характеристики.
-преобразование.
Суть метода состоит в переходе от
аналоговой передаточной функции фильтра
к цифровой на основании отражения нулей
и полюсов. Метод имеет схожие ограничения
с методом инвариантного преобразования
импульсной характеристики. -
Билинейное
 -преобразование.
Суть метода состоит в переходе от
аналоговой передаточной функции фильтра
к цифровой с помощью специальной замены
переменной. Метод позволяет синтезировать
любой тип фильтров, получаемые фильтры
эффективны с точки зрения удовлетворения
спецификаций частотной характеристики
и минимальности порядка фильтра, а
также сохраняют свою устойчивость.
-преобразование.
Суть метода состоит в переходе от
аналоговой передаточной функции фильтра
к цифровой с помощью специальной замены
переменной. Метод позволяет синтезировать
любой тип фильтров, получаемые фильтры
эффективны с точки зрения удовлетворения
спецификаций частотной характеристики
и минимальности порядка фильтра, а
также сохраняют свою устойчивость.
Для синтеза БИХ-фильтра был использован
метод билинейного
 -преобразования
классического аналогового фильтра. В
качестве классического фильтра-прототипа
был использован эллиптический фильтр
с частотной характеристикой вида
-преобразования
классического аналогового фильтра. В
качестве классического фильтра-прототипа
был использован эллиптический фильтр
с частотной характеристикой вида
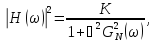
где
 – рациональная функция Чебышева;
– рациональная функция Чебышева;
 – коэффициент, связанный с неравномерностью
в полосе пропускания;
– коэффициент, связанный с неравномерностью
в полосе пропускания;
 – коэффициент передачи фильтра.
– коэффициент передачи фильтра.
Характеристика эллиптического фильтра
имеет равные колебания в полосе
пропускания и подавления (аналогично
оптимальным КИХ-фильтрам). Эллиптическая
характеристика позволяет получить
наиболее эффективные фильтры с точки
зрения соответствия заданной крутизны
амплитудной характеристики и порядка
фильтра. Синтез эллиптического БИХ-фильтра
методом билинейного
 -преобразования
реализован в MATLAB функцией
ellip().
-преобразования
реализован в MATLAB функцией
ellip().
Для оценки порядка БИХ-фильтра нижних
частот применяют графический метод,
подробно описанный в []. Применение
графического метода основано на расчете
двух параметров
 и
и
 :
:


После расчета этих параметров используется
диаграмма оценки порядка эллиптического
фильтра (Рисунок Рисунок 2.3.3.3.2), где
горизонтальная ось – параметр
 ,
вертикальная ось – параметр
,
вертикальная ось – параметр
 ,
порядок фильтра
,
порядок фильтра
 – параметр кривых.
– параметр кривых.

