
Калькулятор расчёта треугольника по трём сторонам
.pdfКалькулятор расчёта треугольника по трём сторонам Автор: Казимиров Леонид Петрович
email: kaslp1939@mail.ru
Москва, 2019г.
Справка.
Здесь решается треугольник по трём сторонам Вершины треугольника обозначаются - 0,1,2, порядок следования - против часовой стрелки.
За -0- может быть принята любая вершина.
В этой вершине (т.0) помещено начало системы координат, ось Х которой направлена по линии 0-1 в сторону вершины 1.
Система координат - правая.
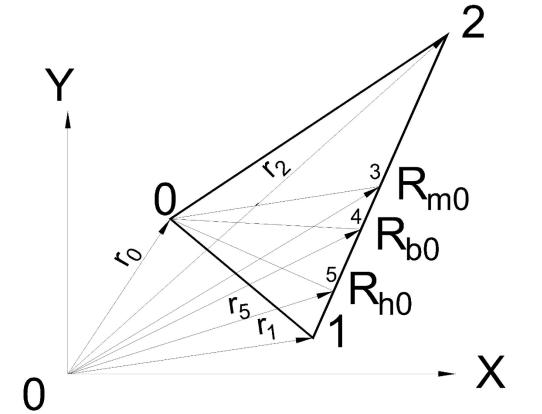
Из каждой вершины на противоположную сторону проведены линии - медиана, бисектриса угла и высота.
Эти линии в месте пересечения оставляют след - точку пересечения.
Для вершины |
0 |
- имеем |
медиана т.3, бисектриса т.4 , высота т.5 |
Для вершины |
1 |
- имеем |
медиана т.6, бисектриса т.7 , высота т.8 |
Для вершины |
2 - имеем |
медиана т.9, бисектриса т.10 , высота т.11 |
|
Для этих точек, а также для вершин треугольника вычисляются координаты в ведённой СК.
Таким образом определяются векторы , начало которых находятся в вершине , а конец - в точке пересечения на противоположной стороне.
Для треугольника также вычисляются - модули этих векторов,периметр и площадь треугольника, радиусы вписанной и описанной окружности, углы при вершинах. Для документирования расчётов имеется возможность делать снимки экрана.
Ссылка на скачивание
«Калькулятор расчёта треугольника по трём сторонам.rar»
https://cloud.mail.ru/public/4NRY/4ViodVedZ
Руководство пользователя
В архиве находится папка «Калькулятор расчёта треугольника по трём сторонам»
сфайлами:
1.CalcTriAngleVektor.exe
2.TriAngleMainVektor.dll
Запускаем CalcTriAngleVektor.exe
Появляется окно
1
Здесь читаем краткую справку о программе. Далее жмём кнопу «Ок».
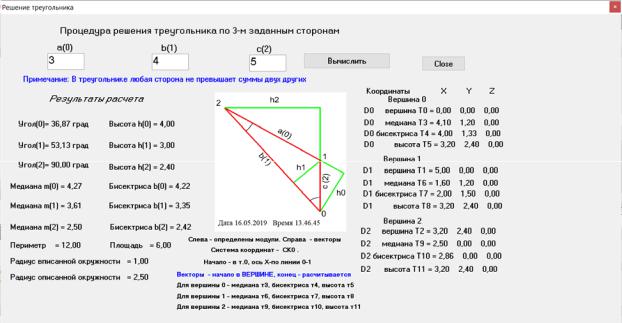
Появляется следующее окно, главное, в котором вводим исходные данные
В нём есть окна a(0), b(1), c(2), для ввода исходных данных, кнопки «Вычислить», «Close» и «Снимок экрана».
Вводим значения a(0), b(1), c(2), и нажимаем кнопку «Вычислить». Получаем результат
2
Использована литература:
Бронштейн И.Н и Семендяев К.А. Справочник по математике М.,1964 г., стр. 186.
Как работает программа
Все рассматриваемые системы координат – правые.
Проведенные из каждой вершины (угла) на противоположную сторону - высота, медиана и бисектриса - создают на этой стороне характерные точки. Координаты этих точек будут координатами соответствующих векторов – высоты, медианы и бисектрисы. Ниже приведен порядок действий для вычисления этих координат.
Введём основную систему координат СКО с центром в вершине (угле) 0, ось X совпадает с линией 0-1 ( с угла 0 к углу 1).
Аналогично введём системы координат в т.1 и т.2.
В каждой из этих систем находим координаты точек - T0,T1,T2 и координаты проведенных - высот, медиан и бисектрис. Далее путём преобразований находим эти координаты в основной СКО. Системы координат показаны на рисунке ниже
3
Вершина 0 (начало координат в т.1) |
Вершина1 (начало координат в т.2) |
|
Y1 
0
|
c |
|
|
b |
|
|
|
1 |
5 |
4 |
3 |
|
a |
2 |
|
X |
Rh0 |
R |
|
R |
X |
||
|
|
|
m0 |
|
|
1 |
|
|
|
b0 |
|
|
|
|
|
Y
Y2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
a |
|
c |
|
|
|
|
|
|
|
2 |
b |
|
0 |
8 |
X2 |
R6 |
7 |
R |
|||
|
m1 R |
|
h1 |
|
|
|
|
b1 |
|
|
|
|
|
Y |
|
Вершина 2 (начало координат в т.0) |
||||||
2 |
|
0 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
Rh2 |
|
|
|
|
|
9 |
c |
|
|
|
|
|
|
|
|
|
|
|
|
||
11 |
0 |
R |
10 |
R |
|
1 |
X |
|||
|
|
|
|
|
m2 |
|
0 |
|||
|
|
|
|
b2 |
|
|
|
|||
Индексы, например у высоты h0 - , обозначает то, что эта высота опущена с вершины угла 0. Аналогично для других вершин и параметров.
Все эти построения СК оправданы тем, что координаты векторов в этих системах координат имеют самый простой вид. Приведение их к основной СКО осуществляется путём поворота СК на соответствующий угол и переноса начала в точку 0.
Чтобы получить вектор, например, высоты h0 в произвольной СКО, определяем вектор R0 начальной точки ( принимается вершина 0 - её координаты) и вектор конечной точки Т5 – её координаты.. Далее из векторного уравнения (см. рисунок)
r0 + Rh0 = r5
находим Rh0.
4
Ссылка на скачивание
Калькулятор расчёта треугольника по трём сторонам.rar
https://cloud.mail.ru/public/4NRY/4ViodVedZ
Для тех кто программирует.
Разработана Динамическая библиотека TriAngleMainVektor.dll
Программа написана на ДЕЛФИ для Windows x32
Ссылка на скачивание CalcTriAngleHVektor.rar
https://cloud.mail.ru/public/3eqH/4h659RyPR
5
