методички / 4042 ЭИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Автоматика, телемеханика и связь на железнодорожном транспорте»

ПРЕДИКТОР СМИТА В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Методические указания к выполнению практической работы по дисциплине

«Теория автоматического управления»

для студентов специальности 23.05.05 «Системы обеспечения движения поездов» специализаций «Автоматика и телемеханика на железнодорожном транспорте», «Телекоммуникационные системы и сети железнодорожного транспорта» очной формы обучения

Составитель: В. Л. Бажанов

Самара

2016

1

УДК 517.2, 62-50

Предиктор Смита в замкнутых системах автоматического регулирования :

методические указания к выполнению практической работы по дисциплине «Теория автоматического управления» для студентов специальности 23.05.05 «Системы обеспечения движения поездов» специализаций «Автоматика и телемеханика на железнодорожном транспорте», «Телекоммуникационные системы и сети железнодорожного транспорта» очной формы обучения / составитель : В. Л. Бажанов. – Самара: СамГУПС, 2016. – 14 с.

Методические указания направлены на изучение предиктора Смита как средства повышения качества управления запаздывающими объектами и объектами высоких порядков. Раскрывается принцип работы предиктора. Разбираются теоретические и технические проблемы реализации предиктора в цифровых управляющих устройствах. Осваиваются приемы практического применения предиктора.

Задание на выполнение работ предусматривает использование вычислительной техники и специализированных прикладных программ для исследования качества работы замкнутых систем управления и оценки эффективности применения предиктора Смита.

Утверждены на заседании кафедры «Автоматика, телемеханика и связь на железнодорожном транспорте» 12 января 2016 г., протокол № 5.

Печатаются по решению редакционно-издательского совета университета.

Составитель: Бажанов Владимир Леонидович

Рецензенты: д. т. н., профессор, заведующий кафедрой «МАП» СамГУПС О. А. Кацуба; к. т. н., профессор кафедры «АТ и С на железнодорожном

транспорте» СамГУПС В. Б. Леушин

Под редакцией составителя

Подписано в печать 17.06.2016. Формат 60.90 1/16. Усл. печ. л. 0,88. Заказ 113.

© Самарский государственный университет путей сообщения, 2016

2

ПРЕДИКТОР СМИТА В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ (САР)

Введение

Запаздывающая реакция управляемых объектов на воздействия регулятора резко снижает качество работы автоматических систем, реализующих принцип управления «по отклонению». Это объясняется тем, что усилия регулятора по противодействию возмущениям, действующим на объект, остаются в течение некоторого времени tz (времени задержки, или запаздывания) полностью безрезультатными. При этом возмущения продолжают свое негативное воздействие на объект, и все дальше уводят его от желаемого состояния. Чем продолжительнее запаздывание, тем больше становится ошибка управления.

Дополнительные сложности при управлении запаздывающим объектом, создает эффект дезинформации, возникающий из-за отсутствия ожидаемой реакции объекта на изначально сформированное регулятором управление. Регулятор провоцируется на дополнительные, более резкие, избыточные воздействия. Отменить эти ошибочные воздействия уже невозможно. Их последствия неотвратимы. Попытки исправления приводят к новым, еще более грубым ошибкам. В итоге система автоуправления утрачивает работоспособность.

Эффективным средством повышения качества управления запаздывающими объектами является предиктор Смита, изучаемый в настоящих методических указаниях.

В результате усвоения теоретического материала, включенного в методические указания, учащиеся будут знать, в каких случаях следует применять предиктор Смита, на каком принципе основано действие предиктора, какие технические средства необходимы для его реализации. Выполнившие полностью предлагаемые практические задания будут уметь корректно выполнять настройку предиктора в зависимости от динамических свойств управляемого объекта, обеспечивать повышенное качество работы систем автоматического управления запаздывающими объектами и объектами высоких порядков. Будут владеть методиками расчета оптимальных параметров предиктора Смита, навыками применения специализированного программного обеспечения, приемами практической настройки систем автоматического управления на основе регуляторов, использующих предиктор Смита.

Изучаемый материал помогает студентам обрести следующие компетенции: ПК-21: умение анализировать технологический процесс эксплуатации, технического

обслуживания и ремонта систем обеспечения движения поездов как объекта управления; ПК-29: умение проводить научные исследования и эксперименты; анализировать,

интерпретировать и моделировать в областях проектирования и ремонта систем обеспечения движения поездов;

3

ПК-30: умение составлять описания проводимых исследований и разрабатываемых проектов, собирать данные для составления отчетов, обзоров и другой технической документации;

ПК-31: владение способами сбора, систематизации, обобщения и обработки науч- но-технической информации, подготовки обзоров, аннотаций, составления рефератов, отчетов и библиографий по объектам исследования; наличием опыта участия в научных дискуссиях и процедурах защиты научных работ и выступлений с докладами и сообщениями по тематике проводимых исследований.

Цель работы: изучение принципа действия предиктора Смита в замкнутых САР; освоение приемов практического применения предиктора при управлении запаздывающими объектами и объектами высоких порядков; оценка эффективности использования предиктора.

Теоретические сведения

Основная идея предиктора

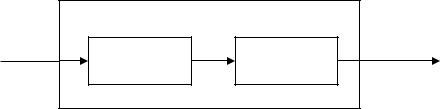
Запаздывающие объекты управления можно представить в виде совокупности двух компонентов, последовательно соединенных между собой. Первый из компонентов – это чистое звено задержки (e-p∙tz), через которое в течение времени запаздывания tz «проходит» каждая поданная регулятором управляющая команда U(t), прежде чем она окажет воздействие на второй компонент – незапаздывающую часть управляемого объекта (W(p)). Такая структура представлена на рис. 1.

на управляющие воздействия регулятора

Общая передаточная функция запаздывающего объекта управления записывается следующим образом:

где W(p)tz – передаточная функция запаздывающего ОУ, W(p) – передаточная функция незапаздывающей части объекта, tz – время запаздывания.

4

Управление, формируемое регулятором в текущий момент, достигнет незапаздывающей части объекта W(p) только спустя время tz. Следовательно, это управление окажется правильным в том случае, если будет рассчитано на основе состояния, в котором объект окажется через время tz. Иначе говоря, регулятору нужен прогноз состояния объекта управления на период tz. При этом регулятор должен настраиваться в расчете на управление незапаздывающим объектом с передаточной функцией W(p). Таким образом, основная идея предиктора заключается в том, чтобы дать регулятору возможность формировать управляющее воздействие на основе прогнозируемого состояния объекта управления [1]. А задача предиктора заключается в расчете этого прогноза.

Что нужно для осуществления прогноза?

Для расчета прогноза микропроцессорному регулятору необходимо иметь:

1.Математическую модель незапаздывающей части объекта управления;

2.Данные о текущем состоянии ОУ;

3.Сведения об управляющих воздействиях, поданных регулятором на объект на последний период tz (они будут влиять на состояние объекта в период времени прогнозирования tz).

Все требуемое для прогноза является вполне доступным. Построение математической модели незапаздывающей части объекта осуществимо любым из известных методов

[2].Датчик регулируемой переменной X(t) доставляет регулятору данные о текущем состоянии управляемого объекта. Сведения об управляющих воздействиях U(t), сформированных самим же регулятором за последний период tz, легко сохраняются в памяти цифрового регулятора.

Действия регулятора, использующего предиктор

Обычный цифровой регулятор без предиктора в каждом очередном временном цикле выполняет следующий набор обязательных действий:

С установленной периодичностью считывает показания с датчика регулируемой переменной X(t);

По запрограммированному закону управления (например, ПИД-закону) рассчитывает коррекцию управляющего воздействия U(t);

Передает результаты расчета на исполнительные органы системы управления для реализации.

Регулятор с предиктором добавляет в описанную выше последовательность действий еще одно действие – определение прогнозируемого состояния объекта управления XP(t). Оно выполняется предиктором Смита после считывания X(t) с датчика. Последующий расчет управления U(t) производится на основе данных прогноза XP(t). Рассчитанное управление выдается на исполнительные органы и обязательно заносится в стеко-

5

вую память регулятора для использования при дальнейшем прогнозе. Требуемый объем стековой памяти зависит от величины времени запаздывания и длительности рабочего цикла регулятора (периода дискретизации). Предиктор Смита реализуется в цифровом регуляторе в виде вычислительного программного модуля.

Указанные действия выполняются регулятором на каждом очередном временном шаге (в каждом цикле).

Еще раз следует подчеркнуть, что регулятор с предиктором должен настраиваться так, будто ему предстоит управлять объектом, не имеющим запаздывания. Это облегчает выбор параметров настройки, поскольку методики определения настроек регуляторов на объектах без запаздывания существенно проще и лучше отработаны.

Эффект от применения предиктора

Применение предиктора Смита обеспечивает пользователю два основных преимущества:

1.Повышенное качество работы замкнутых САР с запаздывающим объектом управления;

2.Простоту расчета оптимальных параметров настройки ПИД-регуляторов при пусконаладке систем управления.

Эффект от применения предиктора зависит от ряда факторов. Главным среди них является точность прогноза, рассчитываемого предиктором. Для получения необходимой точности прогноза требуются:

достоверная информация о текущем состоянии регулируемой переменной;

математическая модель, адекватно описывающая незапаздывающую часть объекта управления.

На практике и первое, и второе неизбежно содержит погрешности. Это означает, что абсолютно точный прогноз невозможен в принципе. Также очевидно, что точность прогноза естественно снижается с увеличением срока прогнозирования (времени запаздывания). Ошибки в прогнозе дезинформируют регулятор, а значит, обрекают его на ошибочные действия. Логично ожидать положительного эффекта от предиктора лишь до тех пор, пока погрешность прогноза не превысит некоторого допустимого предела. Плохо прогнозирующий предиктор может оказаться вреднее, чем его отсутствие.

Неизбежные погрешности в информации от датчика регулируемой переменной и реальная неадекватность математической модели в предикторе всегда будут ограничивать интервал времени [0; tzдоп], на котором обеспечивается необходимая точность прогноза. Если запаздывание у объекта управления tz не превышает величины tzдоп, то положительный эффект от применения предиктора вполне реален. В обратном случае последствия становятся трудно предсказуемыми.

6

Выбор математической модели для предиктора

Универсальные регуляторы (например, ПИД-регуляторы) способны управлять объектами широкого класса. Разнообразие возможных объектов означает, что для точного прогноза предиктор также должен иметь такое же разнообразие прогнозирующих моделей. Можно сразу сказать, что программная реализация опции предиктора с большим количеством математических моделей получится чрезвычайно громоздкой, а практическое использование опции крайне затруднительным. Поэтому для регуляторов массового применения нужен предиктор с минимальным числом прогнозирующих моделей. И лучшим вариантом была бы единая универсальная математическая модель с небольшим числом идентифицируемых параметров, способная с необходимой точностью описывать начальную реакцию всевозможных объектов на воздействия регулятора.

В качестве такой модели может служить неполное дифференциальное уравнение второго порядка с двумя параметрами, легко идентифицируемыми по экспериментальным кривым разгона объектов управления:

Реакция модели (2) на входную ступеньку величиной «U» при нулевых начальных условиях описывается выражением:

Значения параметров Km и Tm у модели (2) должны выбираться так, чтобы выражение (4) с наибольшей точностью описывало начальный участок незапаздывающей части кривой разгона объекта управления. Этим обеспечивается адекватность прогнозирующей модели предиктора объекту управления. Чем больше участок ∆, на котором кривая разгона объекта достаточно хорошо совпадает с переходной характеристикой модели (рис. 2), тем шире диапазон эффективной работы предиктора [0; tzдоп].

Использование в предикторе математической модели (2) оправдывается ее свойствами. Во-первых, для нее сравнительно легко определяются начальные условия, необходимые для расчета прогноза. Они включают в себя текущее значение управляемой переменной X(t), измеряемой датчиком, а также величину ее первой производной dX/dt (оценивается конечно-разностным способом по ограниченной предыстории сигнала). Во-

7

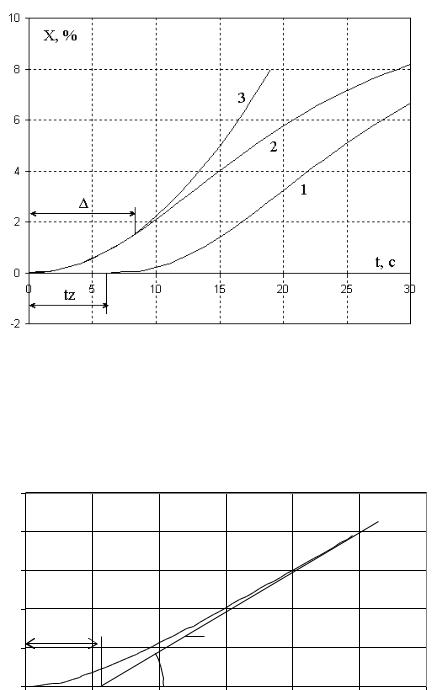
вторых, модель содержит всего два параметра Tm и Km, которые приходится определять при настройке предиктора. Эти параметры наглядно отображаются на переходной характеристике (кривой разгона) математической модели (2), что существенно упрощает оценку их значений. На рис. 3 показано, что асимптота (Ас), проведенная к переходной характеристике, отсекает на оси времени отрезок, равный значению параметра Tm. А тангенс угла наклона асимптоты к оси времени (tgα) численно равен произведению Km∙U (U – величина ступеньки на входе прогнозирующей модели).

Рис. 2. Кривая разгона ОУ с запаздыванием tz – 1; кривая разгона ОУ без учета запаздывания – 2; переходная характеристика математической модели предиктора – 3; интервал удовлетворительного

совпадения кривых 2 и 3 –

8

Зная это, наладчик может провести асимптоту к незапаздывающей части кривой разгона объекта управления и сразу определить по графику значение Тm, а затем найти величину tgα, как отношение противолежащего катета к прилежащему, и рассчитать параметр Km:

m U

Специально разработанная программа визуальной аппроксимации «VAPW» позволяет проще и надежнее определять параметры прогнозирующей модели Tm и Km, при которых реакция модели (2) наилучшим образом аппроксимирует начальный участок незапаздывающей части кривой разгона объекта управления. Программа не только выдает значения искомых параметров Tm и Km, но и позволяет визуально оценивать точность аппроксимации и размер зоны совпадения ∆.

Пример применения предиктора Смита

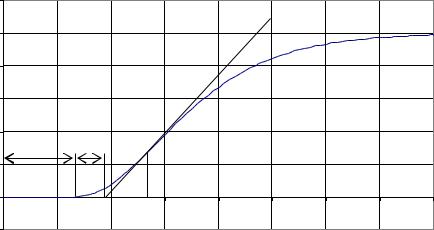
Для практики типична ситуация, когда доступной информацией о свойствах управляемого объекта является экспериментально снятая кривая разгона объекта. Рассмотрим использование предиктора в подобной ситуации. Пусть в распоряжении наладчика системы управления имеется кривая разгона объекта, представленная на рис. 4.

при подаче на вход ступеньки U = 10 %

По изображению кривой разгона видно, что на начальном отрезке времени [0;tz] объект практически не реагирует на входное воздействие. Размер этого участка можно принять за время запаздывания:

9

Кривая при значениях времени t > tz характеризует незапаздывающую часть объекта управления.

Если в предикторе ПИД-регулятора используется прогнозирующая модель (2), то нужно определить значения ее параметров Tm и Km, при которых расчетная реакция модели на входную ступеньку U = 10 % будет наиболее точно совпадать с начальным участком кривой разгона незапаздывающего объекта управления. Проще всего определить Tm и Km, если воспользоваться описанными выше свойствами математической модели (2). Роль асимптоты может исполнить касательная к кривой разгона, проведенная через точку перегиба «а». Тогда значение параметра Tm характеризуется длиной отрезка [tz; b]. На графике видно, что этот отрезок составляет примерно 5,7 секунд, т. е.:

Для определения Km нужно знать тангенс угла наклона касательной «α». Он рассчитывается как отношение противолежащего катета «ас» к прилежащему «bc». Длины катетов определяются по графику, и вычисляется тангенс:

Полученные значения параметров прогнозирующей модели (7) и (9) вводятся в регулятор. Необходимо также указать регулятору величину времени запаздывания tz (срок прогноза). После этого предиктор готов к работе.

Осталось определить параметры ПИД-закона применительно к управлению незапаздывающей частью объекта. Это можно сделать разными способами. Например, можно воспользоваться методом Зиглера–Никольса. Но более надежный результат получается с помощью метода масштабирования. Программа «ММ-настройка», реализующая метод масштабирования, быстро выдает искомый результат:

После ввода настроек (10) ПИД-регулятор с предиктором Смита готов к работе. Систему управления можно запускать в действие.

10