
- •Alexei Yurievich Vinogradov Numerical methods of solving stiff and non-stiff boundary value problems
- •2019 Moscow, Russia
- •Table of contents
- •Introduction.
- •Chapter 2. Improvement of s.K.Godunov’s method of orthogonal sweep for solving boundary value problems with stiff ordinary differential equations.
- •2.1. The formula for the beginning of the calculation by s.K.Godunov’s sweep method.
- •2.2. The second algorithm for the beginning of the calculation by s.K.Godunov’s sweep method.
- •2.3. The replacement of the Runge-Kutta’s numerical integration method in s.K.Godunov’s sweep method.
- •2.4 Matrix-block realizations of algorithms for starting calculation by s.K.Godunov’s sweep method.
- •2.5. Conjugation of parts of the integration interval for s.K.Godunov’s sweep method.
- •2.6. Properties of the transfer of boundary value conditions in s.K.Godunov’s sweep method.
- •2.7. Modification of s.K.Godunov’s sweep method.
- •6.1. The method of "transfer of boundary value conditions" to any point of the interval of integration.
- •6.2. The case of "stiff" differential equations.
- •6.3. Formulas for computing the vector of a particular solution of inhomogeneous system of differential equations.
- •6.4. Applicable formulas for orthonormalization.
- •8.2. Composite shells of rotation.
- •8.3. Frame, expressed not by differential, but algebraic equations.
- •8.4. The case where the equations (of shells and frames) are expressed not with abstract vectors, but with vectors, consisting of specific physical parameters.
- •List of published works.
6.1. The method of "transfer of boundary value conditions" to any point of the interval of integration.
The complete solution of the system of differential equations has the form
 .
.
Or you can write:
 .
.
We substitute this expression for
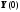 into the boundary conditions of the
left edge and obtain:
into the boundary conditions of the
left edge and obtain:
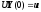 ,
,
 ,
,
 .
.
Or we get the boundary conditions transferred to
the point
 :
:
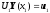 ,
,
where
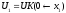 and
and
 .
.
Further, we write similarly

And substitute this expression for
 into the transferred boundary
conditions of the point
into the transferred boundary
conditions of the point
 :
:
 ,
,
 ,
,
 .
.
Or we get the boundary conditions transferred to
the point
 :
:
 ,
,
where
 and
and
 .
.
And so we transfer the matrix boundary condition
from the left edge to the point
 and in the same way transfer the matrix boundary condition from the
right edge.
and in the same way transfer the matrix boundary condition from the
right edge.
Let us show the steps of transferring the boundary conditions of the right edge.
We can write:

We substitute this expression for
 in the boundary conditions of the right edge and obtain:
in the boundary conditions of the right edge and obtain:
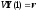 ,
,
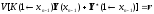 ,
,

Or we get the boundary conditions of the right
edge, transferred to the point
 :
:
 ,
,
where
 and
and
 .
.
Further, we write similarly

And substitute this expression for
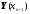 in the transferred boundary
conditions of the point
in the transferred boundary
conditions of the point
 :
:
 ,
,
 ,
,
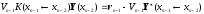 .
.
Or we get the boundary conditions transferred to
the point
 :
:
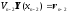 ,
,
where
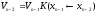 and
and
 .
.
And so at the inner point
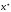 of the integration interval we
transfer the matrix boundary condition, as shown, and from the left
edge and in the same way transfer the matrix boundary condition from
the right edge and obtain:
of the integration interval we
transfer the matrix boundary condition, as shown, and from the left
edge and in the same way transfer the matrix boundary condition from
the right edge and obtain:
 ,
,
 .
.
From these two matrix equations with rectangular horizontal coefficient matrices, we obviously obtain one system of linear algebraic equations with a square matrix of coefficients:
 .
.
6.2. The case of "stiff" differential equations.
In the case of "stiff" differential equations, it is proposed to apply a line orthonormalization of the matrix boundary conditions in the process of their transfer to the point under consideration. For this, the orthonormalization formulas for systems of linear algebraic equations can be taken in [Berezin, Zhidkov].
That is, having received

we apply a line orthonormation to this group of linear algebraic equations and obtain an equivalent matrix boundary condition:
 .
.
And in this line orthonormal equation is substituted
 .
.
And we get
 ,
,
 .
.
Or we get the boundary conditions transferred to
the point
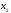 :
:
 ,
,
where
 and
and
 .
.
Now we apply linear orthonorming to this group of linear algebraic equations and obtain an equivalent matrix boundary condition:

And so on.
And similarly we do with intermediate matrix boundary conditions carried from the right edge to the point under consideration.
As a result, we obtain a system of linear
algebraic equations with a square matrix of coefficients, consisting
of two independently stepwise orthonormal matrix boundary conditions,
which is solved by Gauss’ method with the separation of the main
element for obtaining the solution
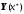 at the point
at the point
 under consideration:
under consideration:
 .
.
