Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Федеральное государственное образовательное учреждение

высшего профессионального образования

“Казанский государственный архитектурно-строительный университет”

Институт транспортных сооружений

Кафедра дорожно-строительных машин

М.Г.Яруллин

Методические указания

для выполнения расчетно-графических работ

для студентов-заочников

Казань – 2012

Задание 1. Исследование структуры и кинематики плоских шарнирно-рычажных механизмов

1.1. Порядок выполнения работы.

1. Начертить тонкими линиями схему механизма в заданном масштабе для 12 положений кривошипа, указанных в задании.

2. Два положения механизма, указанных в задании, обвести основными линиями и для них построить планы скоростей и вычислить масштаб скоростей.

3.  Построить два плана ускорений и вычислить масштаб ускорений.

4. Начертить траекторию центра масс указанного звена, совершающего плоскопараллельное движение, и определить радиусы кривизны этой траектории для двух обведенных положений механизма.

Графическая часть работы выполняется на листе ватмана (миллиметровки) формата А3. На листе располагаются: план положений механизма, 2 плана скоростей и 2 плана ускорений.

В расчетно-пояснительной записки приводится пояснение к построению плана скоростей и плана ускорений для одного положения механизма:

1. Составляются векторные уравнения для определения скоростей и ускорений шарнирных точек.

2. Вычисляются радиусы кривизны траектории выбранного центра масс, угловые скорости и угловые ускорения звеньев для двух выбранных положений механизма.

1.2. Построение плана положений механизма и траекторий точек звеньев

Пусть требуется построить схему механизма, изображенного на рис. 1.1 в масштабе K_L, м/мм, для нескольких положений кривошипа ОА, отмеченных положением принадлежащей ему точки А (А₀, А₁, А₂ и А₃). Положения остальных звеньев механизма, соответствующие заданным положениям кривошипа ОА, находим методом засечек.

Точка В движется по дуге «b–b» окружности радиуса ВС. Ее положение В₁, соответствующее заданному положению кривошипа ОА₁, определяется пересечением дуги «b–b» дугой радиуса  = АВ, проведенной из центра А₁. Положение точки D₁, принадлежащей звену 2, определяется пересечением дуг радиуса ₁ = AD и радиуса ₂ = BD, проведенных соответственно из точек А₁ и В₁. Соединив точку В₁ с точками А₁ и С и опустив перпендикуляр из точки D₁ на отрезок A₁ B₁, получим положения звеньев 2 и 3 в зависимости от заданного положения кривошипа 1. Положение точки F звена 4 определяется пересечением луча D₁E с дугой радиуса D₁F₁. Определив положение точек D₁ и F₁ и, следовательно, звена 4, найдем положение точки S₄.

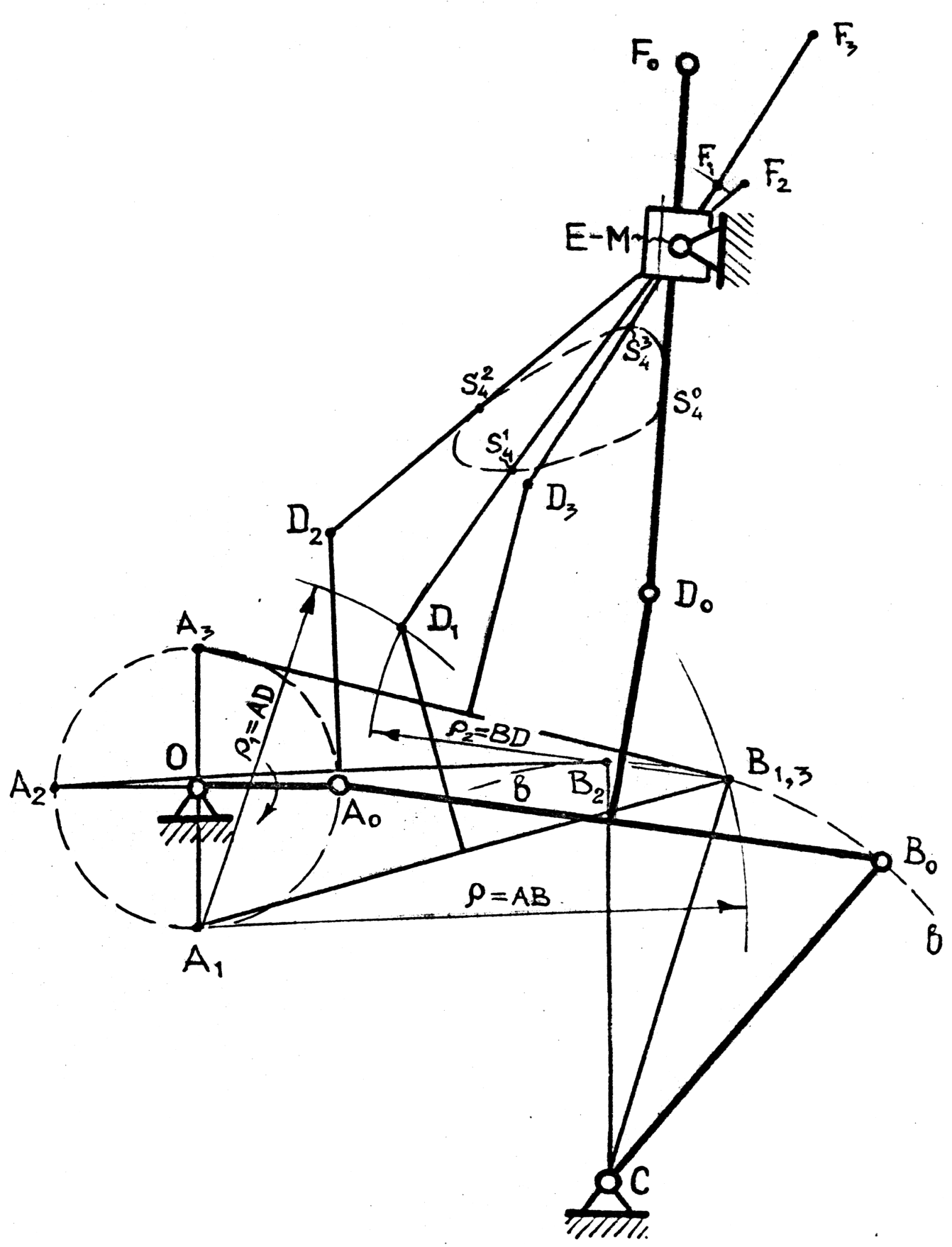
Рис. 1.1. Схема построения положений звеньев механизма

Аналогичным способом вычерчиваются и другие положения механизма. Затем, соединив плавной кривой найденные положения точки, например, S₄ – центра масс звена 4, получим ее траекторию ^*.

1. 3. Построение планов скоростей и ускорений

На рис. 1.2, а представлен механизм, начерченный в масштабе K_L, м/мм. Пусть кривошип 1 этого механизма вращается с постоянной угловой скоростью ₁, 1/c. Требуется определить скорости и ускорения всех точек, указанных на схеме механизма, а также угловые скорости и угловые ускорения его звеньев.

Величина скорости точки А определяется по формуле

V_A = ₁ l_OA, м/с, (1.1)

где l_OA = K_L  ОА – длина кривошипа, м; ОА – отрезок на чертеже, изображающий в масштабе K_L длину кривошипа, мм; а направление – в соответствии с направлением ₁ (перпендикулярно ОА).

Для определения скорости точки В составим векторное уравнение

V_B = V_A + V_B/A. (1.2)

В этом уравнении известны величина и направление вектора , а также направления векторов (  ВС) и (  АВ).

В уравнении (1.2) два неизвестных элемента: величина скорости V_B и V_B/A. А так как векторное уравнение соответствует двум скалярным, то указанное уравнение имеет определенное решение. Для определения этих неизвестных строим многоугольник (план) скоростей (рис. 1.2, б). По указанному в задании (см. 1.10) отрезку оа, изображающему на чертеже скорость V_A, подсчитываем масштаб скорости

K_V = V_A/oa, м/(смм) (оа =70 мм).

Из произвольно взятой на чертеже точки о откладываем отрезок оа перпендикулярно ОА. Через конец этого отрезка (точку а) проводим прямую перпендикулярно АВ, а через точку о – прямую перпендикулярно ВС. Полученная от пересечения этих прямых точка b определяет длины отрезков оb и аb, которые изображают на чертеже скорости V_В и V_B/A. Величины этих скоростей:

V_B = obK_V, м/с; V_B/A = abK_V, м/с.

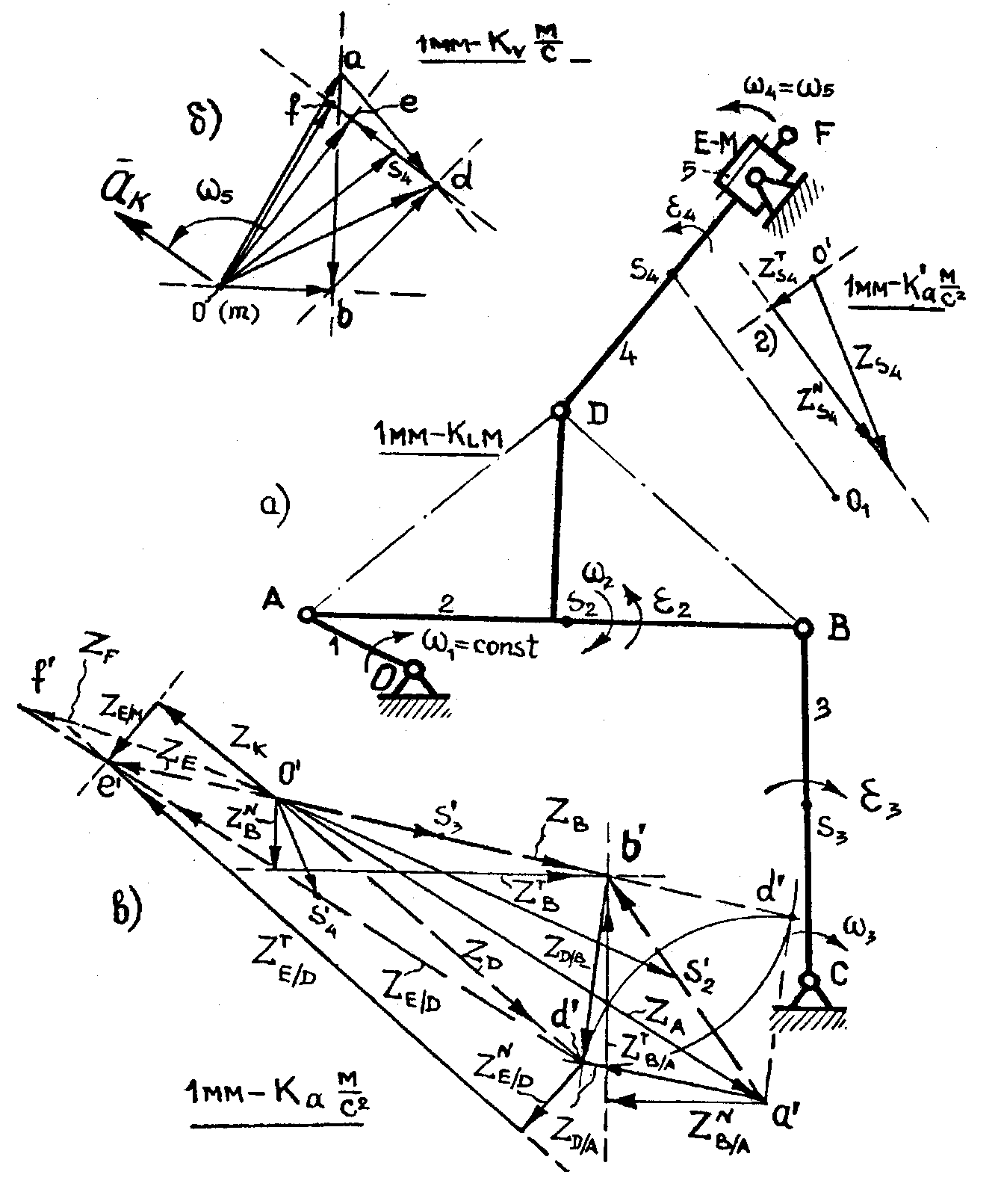
Рис. 1.2. Построение планов скоростей и ускорений

Для определения скорости точки D составим два уравнения:

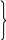V_D = V_A + V_D/A,

(1.3)

V_D = V_B + V_D/B,

и решим их совместно. Для чего через точку a проведем прямую перпендикулярно AD и через точку b – прямую перпендикулярно DB. Пересечение этих прямых определяет точку d, отрезок od и, следовательно, скорость V_D, численное значение которой

V_D = odK_V, м/с.

Скорость точки Е, лежащей на звене 4 и совпадающей в данный момент с неподвижной точкой М механизма, определяется двумя векторными уравнениями:

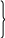V_E =V_D +V_E/D,

(1.4)

V_E = V_M +V_E/M =V_E/M,

так какV_M = 0.

Для решения первого уравнения через точку d проведем прямую перпендикулярно DF, а для решения второго – через точку о (то же и точку m) проведем прямую параллельно DF. При пересечении этих прямых получим точку e, определяющую вектор скорости точки Е и вектор относительной скорости V_E/D. Численные значения скоростей находятся по формулам:

V_E = oeK_V, м/с,

V_E/D = edK_V, м/с.

Скорость точки S₄ определяется из уравнения

V_S4 =V_D +V_S4/D

и скорость точки F – из уравнения

V_F =V_D +V_F/D .

Поскольку V_S4/D /V_E/D = S₄D/ED, V_F/D /V_E/D = FD/ED и, следовательно, V_S4/D = V_E/D  S₄D/ED и V_F/D = V_Е/D FD/ED, то, прибавив в первом случае к вектору (рис. 1.3, б) вектор ds₄ = V_S4/D /K_V = = V_E/D  S₄D/ED K_V =  S₄D/ED, получим вектор скорости точки S₄; во втором случае, прибавив к вектору вектор

fd =V_F/D / K_V = V_F/D FD/ED K_V =ed FD/ED,

получим вектор скорости точки F.

Численные значения этих скоростей:

V_S4 = os₄K_V, м/с,

V_F = ofK_V, м/с.

Теперь найдем угловые скорости звеньев.

Угловая скорость шатуна 2

₂ = V_B/A / l_AB, 1/c,

где l_AB = K_L AB – длина шатуна, м;

то же самое

₂ = V_D/A / l_AD = V_D/B / l_BD, 1/c,

где l_AD = K_L AD и l_{B D} = K_L BD, м.

Угловая скорость балансира 3

₃ = V_B / l_BС, 1/c,

и звена 4 (то же и звена 5)

₄ = ₅ = V_F/D / l_FD ^*, 1/c,

где l_ВС = K_L ВС – длина шатуна 2 и l_FD = K_L F D – длина звена 4, м; l_S4D = K_L S₄ D, м.

Для определения направления угловой скорости, например, звена 4, переносим скорость V_F/D в точку F и рассматриваем движение точки F относительно D в направлении скорости V_F/D. Устанавливаем, что ₄ направлена против хода часовой стрелки. Аналогично, перенеся V_В и V_B/A в точку В, устанавливаем что ₃ и ₂ направлены также против хода часовой стрелки.

Перейдем теперь к определению ускорений.

Ускорение точки А определяется по формуле

а_А = =  l_OA, м/с²,

(так как ₁ = соnst и ₁ = 0) и направлено от точки A к точке О.

Ускорение точки B находится из уравнения

а_B = + + .

А так как точка В движется по окружности, то ее ускорение будет складываться из нормального ускорения и тангенциального ускорения , т. е.

а_B = + ,

поэтому окончательно будем иметь

 + = + + . (1.5)

где  СВ и  АВ.

В этом уравнении а_А получено выше, а и находятся по формулам

= /l_BC, м/с², и = /l_AB, м/с².

Для решения уравнения (1.5) из произвольно взятой точки о’ (рис. 1.2, в) по направлению (параллельно BC по направлению от точки B к точке С) отложим отрезок

= /K_a, мм,

где K_а – произвольно взятый масштаб ускорения ^*, м/(с²мм). Через его конец проводим прямую перпендикулярно ВС. Затем из точки о' параллельно ОА (по направлению от точки А к точке О) отложим отрезок z_A = a_A / K_a, мм.

Из его конца параллельно АВ (по направлению от точки В к точке А) отложим отрезок = /K_a, мм, и через его конец проведем прямую перпендикулярно АВ. Пересечение проведенных прямых даст точку b, которая определяет длины отрезков и , которые в масштабе K_A изображают тангенциальные ускорения и . Численное значение этих ускорений

= K_a  , м/с², и = K_a  , м/с².

Ускорения а_B и а_B/А изобразятся на чертеже отрезками z_B и z_B/А, а их величины найдутся по формулам

а_B = K_a  z_B, м/с², и а_B/А = K_a  z_B/А, м/с².

Угловые ускорения звеньев 2 и 3 находятся по формулам

₂ = /l_AB, 1/c², и ₃ = /l_BС, 1/c².

Для установления направления ₂ и ₃ перенесем ускорения и в точку В и, рассматривая движение В относительно точек А и С, установим, что ₂ направлено против часовой стрелки, а ₃ – по часовой стрелке.

Ускорение точки D находим из уравнений

а_D = а_А + а_D/А,

а_D = а_B + а_D/B,

где а_D/А / а_В/А = AD / AB и а_D/B / а_В/А = DB / AB,

или же а_D/А = а_В/А  AD / AB и а_D/B = а_В/А DB / AB.

Тогда z_D/A = а_D/А / K_a = z_B/A  AD / AB, мм, и z_D/В = а_В/А / K_a = = z_B/A  DВ / AB, мм.

Описываем этими отрезками как радиусами окружности вокруг точек а и b. Пересечение этих окружностей дает две точки d . Из них правильной является та, которая образует с точками а и b треугольник, у которого точки d , b и а располагаются по обходу (по направлению углового ускорения ₂) в том же порядке, что и на шатуне 2 (треугольник ADB) ^*. Соединив точку d  с точкой о, получим отрезок z_D, который в масштабе K_a изображает на чертеже ускорение точки D. Численное значение ускорения а_D = K_a  z_D, м/с².

Для определения ускорения точки Е, принадлежащей звену 4 и совпадающей в данный момент с неподвижной точкой М, составим два уравнения

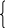 а_E =а_D + + ,

 а_E = а_M +а_E/M +а_K =а_K +а_E/M,

где  DF, а_E/M  DF.

Нормальное ускорение и ускорение Кориолиса определяются по формулам = / l_ED, м/с², и а_K = 2₅V_E/M, м/с².

Для выявления направления а_K необходимо повернуть вектор V_Е/М на 90° в сторону ₅ (см. рис. 1.2, б).

Выполнив расчеты, приступаем к графическому решению уравнений, определяющих ускорение точки D (рис. 1.2, б). Для этого от точки d ' откладываем отрезок

zⁿ_E/D = аⁿ_E/D /K_a, мм,

параллельно ED, направляя его от точки Е к точке D. Через конец этого отрезка проводим прямую линию перпендикулярно ED(DF). Затем из точки о' параллельно а_K откладываем отрезок

z_K = а_K /K_a, мм,

и через его конец проводим прямую параллельно ED. Пересечение указанных прямых дает точку e', которая определяет отрезки и z_E/M, изображающие на чертеже ускорения и a_E/M. Численные их значения

= K_a  z^_E/D, м/с², и a_E/М = K_a  z_E/М, м/с².

Ускорение точки Е изображается на чертеже отрезком z_E, а его численное значение определяется по формуле

а_E = K_a  z_E, м/с².

Ускорения точек S₄ и F найдем из уравнений

а_S4 = а_D + а_S4/D,

а_F = а_D + а_F/D,

причем а_S4 / а_E/D = S₄D / DE и а_F/D / а_F/D = FD / DE, и, следовательно,

а_S4 = а_E/D  S₄D / DE и а_F/D = а_E/D  FD / DE.

Прибавив к o'd ' отрезок

d's₄ = а_S4/D / K_a = z_E/D  S₄D / DE, мм,

и отрезок

d' f’ = а_F/D / K_a = z_E/D  S₄D / DE, мм,

получим отрезки o's'₄ и o'f ', которыми изображаются на чертеже ускорения а_S4 и а_F. Численные значения ускорений

а_S4 = K_a z_S4, м/c², и а_F = K_a z_F, м/с².

Угловое ускорение звена 4 (звена 5)

₄ = ₅ = / l_ED, 1/c²,

где l_ED = K_L ED, м.

Перенос ускорения в точку Е (точку М) показывает, что ₄ направлена против часовой стрелки.

Рассмотрим построение планов скоростей и ускорений для механизма, представленного на рис. 1.3, а. Масштаб длины K_L, м/мм, а также угловая скорость кривошипа 1 известны.

Зная ₁, находим скорость

V_A = ₁ l_OA, м/с,

которая на плане скоростей (рис. 1.3, б) изображается отрезком оа.

Рис. 1.3. Второй случай построения планов скоростей и ускорений

Затем определяем скорость точки В, которую можно рассматривать как состоящую из переносной скорости точки А (V_A) и относительной скорости точки B вокруг точки A (V_B/A), т.е.

V_B = V_A +V_B/A,

где V_B  OB и V_B/A  АВ.

Для решения этого уравнения из точки о проводим прямую параллельно ОВ, а через точку а – прямую перпендикулярно АВ. Точка b пересечения указанных прямых определяет длины отрезков оb и аb, изображающих скорости V_B и V_B/A. Скорость точки С найдем из уравнения

V_С =V_A +V_С/A,

где

V_С/A = V_В/A АС / АВ,

поскольку

V_С/A / V_В/A = АС / АВ.

В соответствии с этим уравнением, прибавив к отрезку оа по направлению оb отрезок

ас = V_С/A / K_V = аb АС / АВ, мм,

получим отрезок ос, изображающий скорость V_С.

Теперь найдем скорость точки D. Движение точки D можно рассматривать как движение, состоящее из переносного со скоростью V_C и относительного со скоростью V_D/C, направленной вдоль DE. Тогда

V_D =V_C +V_D/C,

где V_D  DE и V_D/C  DE.

Поэтому через точку о проводим прямую перпендикулярно DЕ и через точку с – прямую параллельно DE. Точка пересечения прямых определяет точку d и отрезки оd и сd, которые изображают на чертеже скорости V_D и V_D/C.

И, наконец, скорость точки F (рис. 1.3, а):

V_F /V_D = EF/ED.

Отсюда

V_F = V_D EF/ED.

На плане скоростей (рис. 1.3, б) эта скорость изображается отрезком

of = V_F / K_V = od EF / EC,

совпадающим по направлению с отрезком od.

Численные значения скоростей определяются перемножением масштаба скорости и соответствующего отрезка (см. анализ предыдущего механизма).

Угловые скорости звеньев

₂ = V_B/A / l_AB = V_C/A / l_AC, 1/c,

₄ = ₅ = V_D / l_ED = V_F / l_EF, 1/c.

Перенеся скорость V_B/A в точку В (или скорость V_C/A в точку С), устанавливаем, что ₂ направлена против часовой стрелки; а перенеся скорость V_D/E в точку D (или то же самое скорость V_F в точку F), получаем, что ₄ (то же и ₅) направлена по часовой стрелке.

Приступаем к определению ускорений. Ускорение точки А

а_А = =  l_OA, м/с²,

и направлено от точки А к точке О.

Для определения ускорения точки B составим уравнение

а_B = а_А + + ,

где а_B  ОВ,  АВ и = /l_AB, м/с², – нормальная составляющая относительного ускорения; направлена от точки В к точке А.

В соответствии с векторным уравнением через точку о' (рис. 1.3, в) проведем прямую параллельно ОВ. Затем из той же точки о' отложим отрезок

z_А = а_А / K_a, мм,

и к концу его прибавим отрезок

= / K_a, мм,

направив его параллельно АВ от точки B к точке А. Через конец этого отрезка проведем прямую перпендикулярно АВ до пересечения с первой прямой и получим точку b' и отрезки o'b' (z_B) и , которые изображают на чертеже ускорения а_B и .

Ускорение точки С найдем из уравнения

а_С = а_А + а_С/А.

Входящее сюда ускорение а_С/А определяется из пропорции

а_С/A / а_В/A = АС / АВ,

и, следовательно,

а_С/A = а_В/A АС / АВ.

Отложив на плане ускорений от точки а отрезок

a' c' = а_C/A / K_a = z_B/A  AC / AB, мм,

совпадающий с отрезком z_B/A, получим точку с' и отрезок о'с' (z_C), изображающий ускорение точки С.

Ускорение точки D, принадлежащей кулисе – звену 5, определяется уравнением

 а_D = а_C + а_D/C + а_K.

Так как точка D движется по окружности, то

а_D = +

и предыдущее уравнение примет вид

 + а^_D = а_C + а_D/C + а_K,

где

 DE, а_D/C  DE, = / l_DE, м/с², = / K_a и

а_K = 2₄V_D/С

– ускорение Кориолиса, направление его определяется поворотом вектора V_D/C на 90° в сторону ₄ (показано на рис. 1.3, б).

Выполнив вычисления, переходим к графическому решению уравнения, для чего из точки о' (рис. 1,3, в) откладываем параллельно DF (в направлении от точки D к точке Е) отрезок и  DE; из точки с' – z_K = a_K / K_A, мм. Через конец этого отрезка проведем прямую параллельно DE. Пересечение указанных прямых будет в точке d'. Отрезки , z_D/C и о'd '(z_D) изображают ускорения , а_D/C и а_D.

Ускорение точки F найдем из выражения

а_F / а_D = EF / ED,

откуда

а_F = а_D  EF / ED.

Это ускорение на плане ускорений изображено отрезком

z_F = а_F /K_a = z_D  EF/ED, мм.

Для определения численных значений ускорений необходимо полученные отрезки из плана ускорений умножить на масштаб ускорения (см. анализ первого механизма).

Угловые ускорения звеньев

₂ = /l_AB, 1/c², и ₄ = ₅ = / l_ED, 1/c².

Перенос ускорения а^_B/А в точку В показывает, что ₂ направлено против часовой стрелки, а перенос ускорения в точку D устанавливает, что ₄ (то же самое ₅) направлено по часовой стрелке.

Сравнивая направления ₂ и ₂, а также ₅ и ₅, видим, что звенья 2 и 5 движутся ускоренно, сравнение же V_B и а_B показывает, что ползун 3 движется замедленно.