
- •Часть I
- •1. Цели и задачи курса “Основы векторного и тензорного анализа” (овта), и его место в учебном процессе.
- •Элементы векторной алгебры
- •Градиент скалярного поля
- •Дивергенция векторного поля и теорема Остроградского-Гаусса
- •Ротор векторного поля и теорема Стокса
- •Комбинированные задачи векторного анализа
- •Задачи на использование метода оператора набла
- •Перечень рекомендованной литературы
Градиент скалярного поля
Если в каждой точке
![]() пространства задан скаляр
пространства задан скаляр
![]() – это скалярное
поле. Если
в каждой точке
пространства задан вектор
– это скалярное
поле. Если
в каждой точке
пространства задан вектор
![]() – это векторное
поле.
– это векторное
поле.
Если скалярное
поле
задается в ДСК,
то это означает, что скалярная функция
трех переменных
![]() .
При рассмотрении локального поведения
часто используется порождаемое
им векторное поле
.
При рассмотрении локального поведения
часто используется порождаемое
им векторное поле
![]() ,
называемое градиентом
скалярного поля.
,
называемое градиентом
скалярного поля.
Одно из альтернативных
определений этой величины использует
понятие производной
по направлению,
заданному единичным вектором
![]() .
.
Градиентом скалярного поля в точке называется вектор
 , (2.1)
, (2.1)
величина которого
определяется производной по направлению
единичного вектора
нормали к поверхности уровня
![]() ,
проходящей через точку
,
в сторону возрастания значений
.
,
проходящей через точку
,
в сторону возрастания значений
.
Напомним, что нормалью к поверхности S в точке P называется прямая, проходящая через точку P и перпендикулярная к касательной плоскости к S в этой точке.
Компоненты этого
вектора в ДСК
 можно получить, используя приводимое
ранее выражение
.
можно получить, используя приводимое
ранее выражение
.
Следовательно, в ДСК выражение для градиента скалярного поля имеет вид:
 (2.2)
(2.2)
Полный дифференциал
![]() от
определяется как приращение значения
этой величины при изменении радиус-вектора
на бесконечно малое приращение
от
определяется как приращение значения
этой величины при изменении радиус-вектора
на бесконечно малое приращение
![]() (2.3)
(2.3)
Следовательно,
 , (2.4)
, (2.4)
где
![]() – угол между векторами градиент
– угол между векторами градиент
![]() и
и
![]() .
Следовательно, направление
вектора
– это направление скорейшего роста
скалярного поля в данной точке, а модуль
градиента – это скорость роста поля в
этом направлении.
.
Следовательно, направление
вектора
– это направление скорейшего роста
скалярного поля в данной точке, а модуль
градиента – это скорость роста поля в
этом направлении.
Экстремальные
точки скалярного поля
– это точки, при смещении из которых с
точностью до членов, линейных по смещению,
поле остается неизменным. Из этого
определения вытекает, что частные
производные
в этих точках равны нулю, а возникающую
из этого условия систему трех уравнений
можно использовать для нахождения
экстремальных
точек
.
По этой же причине в этих точках
![]() .
.
Указания по решению задач
2.1. Для заданных ниже функций найти градиент, точки экстремума, направление наискорейшего роста в заданной точке (x0, y0, z0), а также уравнение плоскости, касательной к поверхности постоянного значения функции в этой точке:
2.1.1.
![]() ;
;
2.1.2.
![]() ;
;
2.1.3.
![]() ;
;
2.1.4.
![]() ;
;
2.1.5.
![]() .
.
Указание. Пусть = (2.1.3). Для нахождения компонент вектора градиента и точек экстремума вычислим:

Запишем систему уравнений, определяющих точки экстремума:

Решение полученной
системы определяет точку экстремума
с координатами
![]()
Выражение для векторного поля градиента имеет вид:
 ,
,
а в точке
![]() :
:
![]() .
.
Для нахождения
уравнение плоскости, касательной к
поверхности постоянного значения
в точке
![]() воспользуемся определяющим ее выражением
(1.22), в котором компоненты вектора
воспользуемся определяющим ее выражением
(1.22), в котором компоненты вектора
![]() заменим на соответствующие значения
компонент вектора
заменим на соответствующие значения
компонент вектора
![]() :
:
![]() .
.
2.2. Найти компоненты вектора градиент:
2.2.1.
![]() ,
где
,
где
![]() .
.
Указание.
В данной задаче
=
![]() .
.

Следовательно: 
Аналогично: 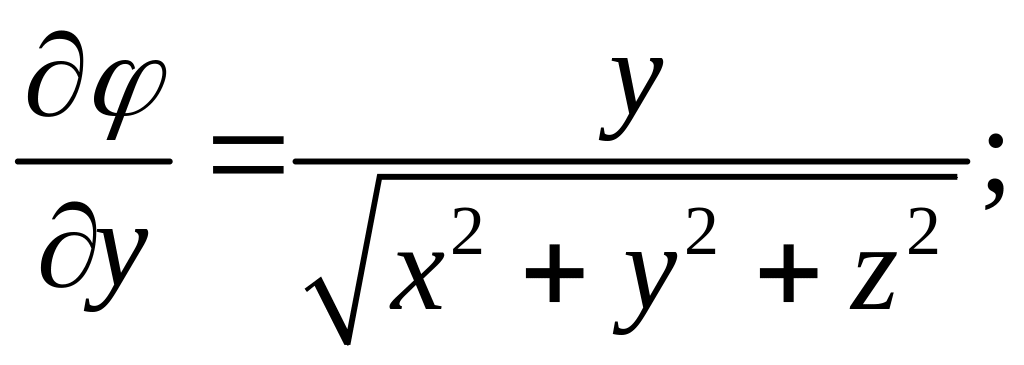
и 
Подставляя найденные выражения в (2.2), получим:

Ответ:
![]() .
.
2.2.2.
![]() ,
где
,
где
![]() ;
;
Указание.
Решение данной задачи аналогично решению
предыдущей. Следует лишь учесть, что в
соответствии с определением, данным
при постановке задачи, вектор
![]() .
.
Итак:
=
![]() .
.
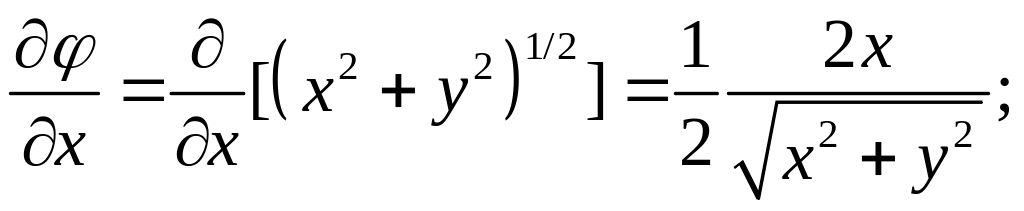
Следовательно: 
Аналогично: 
а ![]()
Подставляя найденные выражения в (2.2), получим:
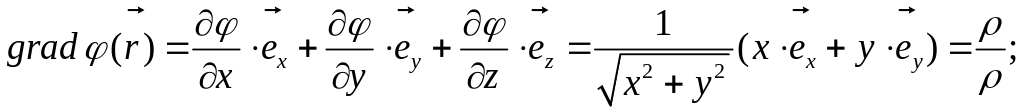
Ответ:
 .
.
2.2.3.
![]() ;
;
2.2.4.
![]() ;
;
2.2.5.
 ,
где
,
где
![]() — постоянный вектор,
— постоянный вектор,
![]() ;
;
2.2.6.
![]() ,
где
,
где
![]() — постоянный
вектор,
— постоянный
вектор,
![]() ;
;
2.2.7.
![]() ;
;
Указание.
В данной задаче
=
![]() .
.

Следовательно: 
Аналогично: 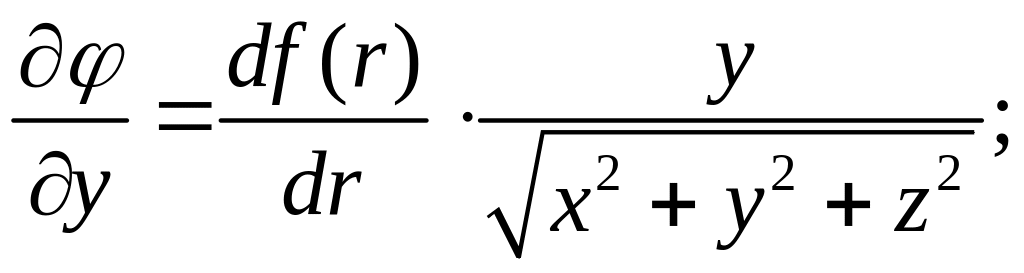
и 
Подставляя найденные выражения в (2.2), получим:
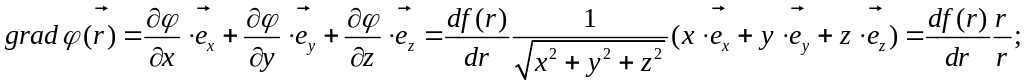 Ответ:
Ответ:
![]() .
.
2.2.8.
![]() ;
;
2.2.9.
![]() ,
где
,
где
![]() — постоянный вектор;
— постоянный вектор;
2.2.10.
![]() ;
;
2.2.11.
![]() ;
;
Указание.
В данной задаче
=
![]() .
.
 Следовательно:
Следовательно:

Аналогично: 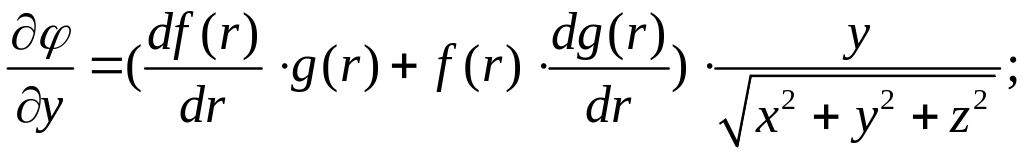
и 
Подставляя найденные выражения в (2.2), получим:

![]()
Ответ:
![]() .
.
2.2.12.
![]() ,
где
,
где
![]() — постоянный вектор.
— постоянный вектор.
Указание.
В данной задаче
=
![]() =
=
![]() .
.
![]()
Следовательно: ![]()
Аналогично: 
и ![]()
Подставляя найденные выражения в (2.2), получим:

Ответ:
![]() .
.
2.2.13.
![]() ,
где
и
,
где
и
![]() — постоянные векторы;
— постоянные векторы;
Указание. В данной задаче
=
![]() =
=
![]() .
.
![]() ,
,
где
![]() компонента векторного произведения на
ось x.
компонента векторного произведения на
ось x.
Примечание: Полученный результат можно получить быстрее, переписав, используя свойство векторного произведения по отношению к циклической перестановке векторов, выражение для в виде:
=
=![]() =
=![]()
Следовательно: ![]()

![]()
Подставляя найденные
выражения в (2.2), получим:
![]()
Ответ: .
2.2.14.
![]() ;
;
2.2.15.
![]() ;
;
2.2.16.
![]() ;
;
2.2.17.
![]() ;
;
2.2.18.
![]() ;
;
2.2.19.
![]() ;
;
2.2.20.
![]() ;
;
2.2.21.
![]()
2.2.22.

2.2.23.
![]()
2.3.1. Написать
уравнение прямой, проходящей через
точку А(3,
2, 1) в направлении наискорейшего роста
функции
![]() ,
r=|
|
,
r=|
|
Указание. Уравнение прямой, проходящей через точку и параллельной вектору , определяется выражением (1.23a). Направление наискорейшего роста функции в точке определяется вектором градиента этой функции в этой точке.
В соответствии с этими замечаниями найдем вначале векторное поле градиента предложенной функции.
В данной задаче = .
 .
.
Следовательно: ![]()
Аналогично: ![]()
и ![]()
Подставляя найденные выражения в (2.2), получим:
![]() .
.
Для определения
значения вектора градиента в точке А(3,
2, 1) введем
радиус-вектор
![]() ,
вычислим его длину
,
вычислим его длину
![]() и подставим в полученное выражение для
градиента:
и подставим в полученное выражение для
градиента:
![]()
![]()
Сократив записанное уравнение на неравный нулю множитель, получим искомое уравнение прямой.
Ответ:
![]() .
.
2.3.2. Написать уравнение плоскости, касательной к поверхности постоянного значения функции (x2+y2-3z) в точке А(-1, 2, -1).
2.3.3. Найти угол между направлениями наискорейшего роста функций (x2+2y2-z2) и r=| | в точке А(-1, 1, 1).
2.3.4. Найти силу, действующую на частицу в точке А(-1, -2, -1), если потенциальная энергия равна (2x+y2-z).
Указание.
По определению,
если задана
потенциальная энергия
![]() ,
сила
,
сила
![]() ,
действующую на частицу в точке
,
определяется выражением
,
действующую на частицу в точке
,
определяется выражением
![]() .
.
2.3.5. Написать
уравнение плоскости, проходящей через
точку А(1,
1, 2), которая является плоскостью,
касательной к поверхности постоянного
значения функции
![]() в этой точке.
— радиус-вектор,
— постоянный вектор с координатами (1,
2, 0).
в этой точке.
— радиус-вектор,
— постоянный вектор с координатами (1,
2, 0).
