Федеральное агентство по образованию

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Положенцев Е. В.

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

по курсу:

ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА

Часть I

Ростов-на-Дону

2010

1. Цели и задачи курса “Основы векторного и тензорного анализа” (овта), и его место в учебном процессе.

Целью данного курса является освоение студентами основ одного из наиболее важных для физической науки разделов математики - векторного и тензорного анализа.

Главной задачей курса является заполнение пробела, существующего между традиционными математическими дисциплинами и дисциплинами теоретической физики, и подготовка студентов к лучшему восприятию последних, а также изложение математических методов, используемых в общей физики, прежде всего в курсе «Электричество и магнетизм». Студенты должны научиться пользоваться изученным математическим аппаратом так, как это принято в физике, освоить типичные для физики приемы его применения и привыкнуть к наиболее распространенным в физической литературе системам обозначений.

Для успешного усвоения курса ОВТА студенты должны знать и уметь использовать основные разделы традиционного математического анализа, векторной алгебры и аналитической геометрии, которые изучаются на первом курсе физического факультета частично раньше, а частично – параллельно с курсом векторного и тензорного анализа.

В первой части курса ОВТА, читаемого студентам первого курса физического факультета в весеннем семестре излагаются основы математического описания дифференциальных и интегральных свойств векторных и скалярных полей. Знание этих свойств и умение владеть соответствующим математическим аппаратом совершенно необходимо для освоения курса общей физики «Электричество и магнетизм» и курсов теоретической физики «Электродинамика» и «Основы механики сплошных сред», где изучаются свойства полевых систем – электромагнитного поля и сплошных сред – жидкостей и твердых тел.

Содержание

1. Элементы векторной алгебры……………………………………………..стр. 4

2. Градиент скалярного поля…………………………………………………стр. 15

3. Дивергенция векторного поля и теорема Остроградского-Гаусса………стр. 25

4. Ротор векторного поля и теорема Стокса…………………………………стр. 35

5. Комбинированные задачи векторного анализа……………………………стр. 42

6. Задачи на использование метода оператора набла………………………..стр. 45

7. Перечень рекомендованной литературы…………………………………..стр. 50

Элементы векторной алгебры

Большинство физических величин являются скалярными или векторными.

Скаляр целиком определяется своим численным вещественным значением (масса, заряд, энергия, работа).

Одно из определений вектора апеллирует к его геометрическому образу – направленному отрезку (или упорядоченной паре точек), который характеризуется своей длиной и направлением.

Д ля указания направления вектора в пространстве необходимо задать материальные ориентиры, т.е. построить систему отсчета. Если в трехмерной системе отсчета выбрать три базовых направления, то мы получаем возможность задавать направление вектора углами, которые он образует с базовыми направлениями. А если к тому же вдоль базовых направлений выбрать линейный масштаб в единицах измерения векторной величины, то получим систему координат, позволяющую задавать вектор тремя независимыми вещественными числами – проекциями вектора на оси координат.

Н аиболее употребительна декартовая система координат (ДСК), при построении которой базовые направления задаются тремя взаимно перпендикулярными прямыми – осями координат . Различают правые (правовинтовые) и левые (левовинтовые) ДСК. В правой ДСК направление оси определяется направлениями осей по правилу правого винта (см. рисунок).

Сложение векторов можно определить геометрическим образом по правилу параллелограмма: суммой векторов и называют вектор , проведенный из начала к концу , если конец и начало совмещены. Операция сложения векторов обозначается следующим образом:

= = (1.1)

и обладает свойством коммутативности (см. рисунок):

А налогичным образом определена и операция умножения вектора на скаляр:

. (1.2)

Модуль (длина) вектора

,

а направление совпадает с направлением вектора , если > 0, и противоположно этому направлению, если < 0.

В ДСК вектор определяется тремя проекциями (компонентами) на соответствующие оси и представляет собой совокупность трех значений, которая обозначается следующим образом: или . Это так называемое алгебраическое представление векторов.

Операции сложения векторов и умножения на скаляр в своей совокупности определяют линейную комбинацию векторов:

. (1.3)

Вводя три единичных вектора (орта) , направленных по соответствующим осям координат, вектор , с учетом (1.3), можно записать в виде его разложения по ортам:

, (1.4)

где индекс суммирования i принимает значения либо x, y, z (при алфавитном способе обозначения осей), либо 1, 2, 3.

В частности, любой точке пространства с координатами и мы можем сопоставить радиус-вектор , проведенный в эту точку из начала координат. Разложение этого вектора в ДСК имеет вид:

. (1.4a)

Пользуясь разложением (1.4) векторов по ортам, сумму векторов и называют вектор = , компоненты которого определяются формулой:

, (1.5)

Соответственно, в результате умножения вектора на скаляр получается вектор , компоненты которого определяются по формуле:

, (1.6)

При определении операций типа произведение векторов в результате мы можем получить либо скалярную, либо векторную величины. В соответствии с этим определены скалярное и векторное произведения двух векторов.

Скалярное произведение векторов.

Скалярное произведение двух векторов обозначается и определяет скалярную величину по формуле:

, (1.7)

где – угол между векторами и . Поскольку есть проекция a_b вектора на направление вектора , то скалярное произведение (1.7) является произведением этой проекции a_b на модуль вектора и, наоборот, произведением модуля вектора на проекцию b_a вектора на направление вектора .

Из определения скалярного произведения следуют следующие его свойства:

1. коммутативность: ;

2. дистрибутивность:

3. возможность вынесения (внесения) скалярных значений за скобки скалярного произведения:

4. скалярное произведение двух ортогональных векторов равно 0.

Последнее свойство, в частности, для ортов означает, что

, (1.8)

где – символ Кронекера. (1.9)

Используя разложения векторов и (1.4), мы можем получить выражение для скалярного произведения через компоненты этих векторов:

,

в котором при суммировании по индексу j мы воспользовались свойством (1.9) символа Кронекера.

Следовательно, скалярное произведение векторов и равно:

, где . (1.10)

Квадрат модуля вектора (квадрат его длины) находится как

,

и, следовательно, сам модуль (длина) определяется следующим выражением

. (1.11)

Компоненты вектора можно определить, используя скалярные произведения

= , где i = x, y, z. (1.12)

Направляющие косинусы этого вектора, в соответствии с (1.12), определяются следующими выражениями:

. (1.12)

Векторное произведение векторов

Векторное произведение двух векторов и обозначается , или и образует вектор , направление которого определяется правилом правого винта, если вектор поворачивать по направлению к вектору , а величина определяется следующей формулой:

, (1.13)

где — единичный вектор, направление которого определяется правилом правого винта.

Из определения векторного произведения (1.13) следуют следующие его свойства:

1. антикоммутативность: ;

2. дистрибутивность:

3. возможность вынесения (внесения) скалярных значений за скобки векторного произведения:

4. векторное произведение двух параллельных векторов равно нулевому вектору , все компоненты которого равны нулю.

Применяя (1.13) к единичным ортам, получим:

; ; ; и

, где индекс . (1.14)

Модуль векторного произведения – это площадь параллелограмма, построенного на векторах-сомножителях, равная:

. (1.15)

Используя разложения векторов и по единичным ортам (1.4) и значения векторных произведений (1.14), легко получить выражение для вектора :

= = (1.16)

Последнее равенство обычно оформляется с помощью символического определителя:

= . (1.17)

Произведения трех векторов

Умножив скалярно вектор на векторное произведение и , получим смешанное произведение векторов (СПВ).

Используя формулы для векторного (1.16) и скалярного (1.10) произведений, легко получить следующие выражение для скалярной величины:

= , (1.18)

Это равенство обычно оформляется с помощью символического определителя:

= (1.19)

Геометрически значение СПВ равно объему V параллелепипеда, построенного на векторах , и . Знак “ ” перед V в (1.19) выбирается в том случае, когда тройка векторов правая, а знак “ ” — в случае, когда тройка векторов левая.

Для любых векторов значение СПВ не меняется при циклической перестановке векторов и меняет знак при перестановке двух любых векторов-сомножителей:

Если хотя бы два вектора-сомножителя коллинеарны, смешанное произведение равно .

Умножив векторно вектор на векторное произведение и , получим двойное векторное произведение , которое вычисляется по правилу, известному под названием «бац минус цаб»:

. (1.20)

Уравнения плоскости и прямой

Уравнение плоскости, перпендикулярной вектору и проходящей через точку , в векторной форме имеет вид:

(1.21)

или в компонентах:

. (1.22)

Уравнение прямой, параллельной вектору и проходящей через точку , имеет вид:

, (1.23)

где  — любое вещественное число. Учитывая, что величина  одна и та же для всех координатных осей, получаем, что, уравнение прямой, записанное в компонентах, имеет вид:

. (1.23a)

Указания по решению задач

1.1. Выразить косинус угла между векторами и через направляющие косинусы этих векторов (направляющие косинусы — косинусы углов между вектором и осями координат).

Указание. Используя определение скалярного произведения (1.7), косинус угла между векторами и , запишем:

= .

Подставляя в полученную формулу выражения (1.12), определяющие значения компонент векторов через их модули и направляющие косинусы с осями координат, получим:

=

= =

= .

Ответ.

1.2. Дан тетраэдр ABCD, где, например, A(1,1,0), B(1,5,0), C(3,1,0), D(2,1,3).

Найти:

1.2.1. Компоненты вектора ;

1.2.2. Длину стороны AB;

1.2.3. Угол между векторами и ;

1.2.4. Площадь грани ABC;

1.2.5. Вектор нормали к грани ABC;

1.2.6 Угол между гранями ABC и ABD;

1.2.7. Объем тетраэдра ABCD;

1.2.8. Уравнение плоскости, параллельной плоскости ABC и проходящей через точку D;

1.2.9. Уравнение прямой, параллельной прямой AB и проходящей через точку C.

Указание. К вершинам тетраэдра ABCD проведем из начала координат радиус вектора (1,1,0), (1,5,0), (3,1,0) и т.д.

Вектора , и т.д. можно получить из выражений типа:

= ; = .

Следовательно, (0,4,0) и (2,0,0).

= ; = .

=

Для вычисления площади грани ABC воспользуемся выражением (1.15):

=4.

Объем пирамиды , где – площадь основания пирамиды, – высота. Если в качестве основания выбрать грань ABC, т.е. = , то высоту пирамиды можно определить выражением = , а для вычисления объема тетраэдра ABCD получить следующую формулу:

= = = =4,

где – единичный вектор нормали к грани ABC.

Другой способ нахождения объема тетраэдра:

1.3. Найти проекции скорости и ускорения точки, а также угол между скоростью и ускорением в заданный момент времени, если координаты x и y заданы, условиями:

1.3.1. x = sin(t²), y = cos(t²), t = 1;

1.3.2. x = sin(t) - cos(2t), y = cos(t²), t = 1;

1.3.3. x = sin²(t), y = cos(t), t = 2.

Указание. Для решения предложенных задач следует ввести радиус-вектор , описывающий положение точки в произвольный момент времени t:

= ,

найти вектор скорости точки :

= = ,

а также вектор ускорения точки :

= = .

В частности, если , а , то:

= ;

= ;

= ;

= .

Подставив полученные выражения для , в формулу для , а выражения для и в формулу для и положив в полученных выражениях значение t = 1, получим значения векторов скорости и ускорения точки при t = 1.

Угол между скоростью и ускорением в заданный момент времени можно определить, используя определение (1.7) скалярного произведения двух векторов.

1.4. Найти координаты центра масс системы трех частиц с массами m₁, m₂ и m₃, расположенных в точках A₁, A₂ и A₃:

1.4.1. m₁ = 2, m₂ = 4, m₃ = 3, A₁ (0,0,2), A₂ (1,1,0), A₃ (0,1,1);

1.4.2. m₁ = 1, m₂ = 2, m₃ = 2, A₁ (1,0,1), A₂ (0,2,3), A₃ (1,1,1);

1.4.3. m₁ = 3, m₂ = 4, m₃ = 1, A₁ (2,0,0), A₂ (1,2,1), A₃ (-1,1,1);

1.4.4. m₁ = 3, m₂ = 1, m₃ = 2, A₁ (-1,0,1), A₂ (2,3,0), A₃ (1,0,2).

Указание. Для решения задачи введем радиус-вектора , указывающие в ДСК положение частицы с номером , при этом = 1, 2, 3 в соответствии с количеством частиц.

В этом случае радиус-вектор , описывающий в ДСК положение центра масс системы N частиц, определяется следующей формулой [1]:

= .

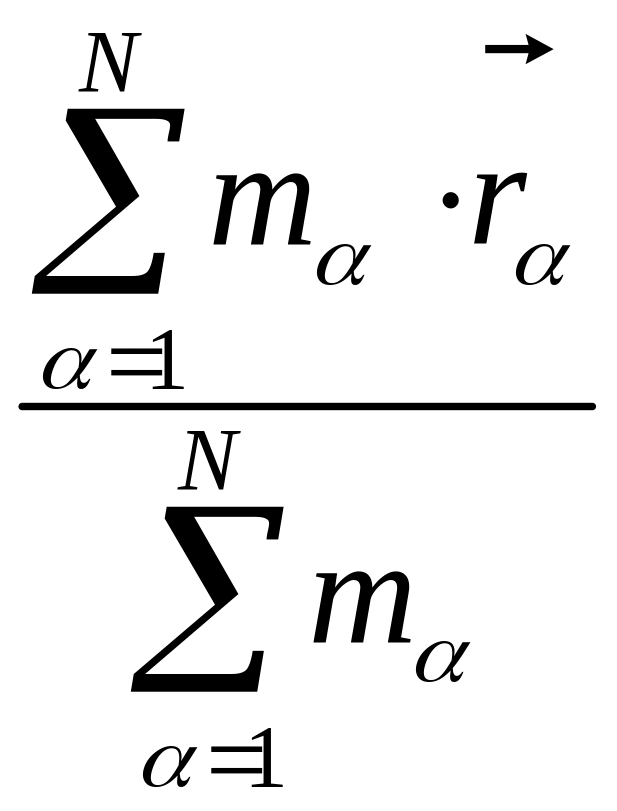Используя это выражение для каждой компоненты , получим значения координат центра масс системы частиц.

1.5. Упростить выражения:

1.5.1. ;

1.5.2. ;

1.5.3. ;

1.5.4. .

1.6. Доказать справедливость тождества:

1.7. Написать уравнение плоскости, проходящей через точку A и перпендикулярной вектору , и уравнение прямой, проходящей через точку A и параллельной вектору :

1.7.1. A(1,2,-3, ), (5,7,-6);

1.7.2. A(-2,0,1, ), (-1,2,4);

1.7.3. A(1,2,-1, ), (0,1,-1).

Указание. Для решения задачи следует воспользоваться выражением (1.22):

,

которое является уравнением плоскости, перпендикулярной вектору и проходящей через точку и выражением (1.23a):

,

которое является уравнением прямой, параллельной вектору и проходящей через точку .

Например, ответы к задаче 1.7.1.

Уравнение плоскости: – ;

Уравнение прямой: – .

1.8. Найти объем параллелепипеда, построенного на векторах:

.