2.1.3. Пример решения задачи 1.

Задача 1. Расчет многопролетной неразрезной балки, свободно опертой на независимые упругие опоры.

Задание.

Определить коэффициент податливости упругой опоры для неразрезной многопролетной балки ( рис. 1-1). Упругой опорой является однопролетная балка 4-5, расположенная перпендикулярно к многопролетной.

Раскрыть статическую неопределимость многопролетной балки. Построить для нее эпюры перерезывающих сил и изгибающих моментов. Схема балки изображена на рис.1.1. Исходные данные приведены в табл. 1.1.

Таблица 1.1.

Исходные данные к задаче 1.

l1/l0	l2/l0	l3/l0	lп/l0	c/l0	I1/I0	I2/I0	I3/I0	Iп/I0	Q1/q0l0	Q3/q0l0	P/q0l0
1,5	1,0	1,2	2,0	0,4	1,0	1,2	1,1	1,3	1,0	1,2	2,0
q0 = 2 кН/м ; l0 = 2 м ; l1 = 3 м ; l2 = 2,4 м ; Q1 = 40 кН ; Q3 = 48 кН ; P = 80кН

Определение коэффициента податливости А₁ упругой опоры.

В еличина коэффициента податливости упругой опоры А₁ многопролетной балки 0 -3 равна прогибу f₁ в точке 1 поперечной балки 4-5, загруженной в этой точке единичной силой R₁= 1 ( рис. 1.2). Пользуясь таблицей изгиба балок [3], находим

Раскрытие статической неопределимости неразрезной балки.

Расчетная схема неразрезной балки приведена на рис.1.3. Для раскрытия статической неопределимости балки используется метод пяти моментов.

Рис. 1.3.Расчетная схема балки

Определение углов поворота опорных сечений балки от внешней нагрузки.

Углы поворота балки α_i в точках 0, 1, 2 ( см. рис.1.3.) находятся с помощью таблиц элементов изгиба свободно опертых балок [1]:

Составление системы уравнений пяти моментов и ее решение.

Уравнения неразрывности углов поворота на опорах имеют вид [2, с. 46]:

Просадка упругой опоры равна

Умножив все члены уравнений (1.1) на 6EI₀/l₀ , получим

для опоры 0

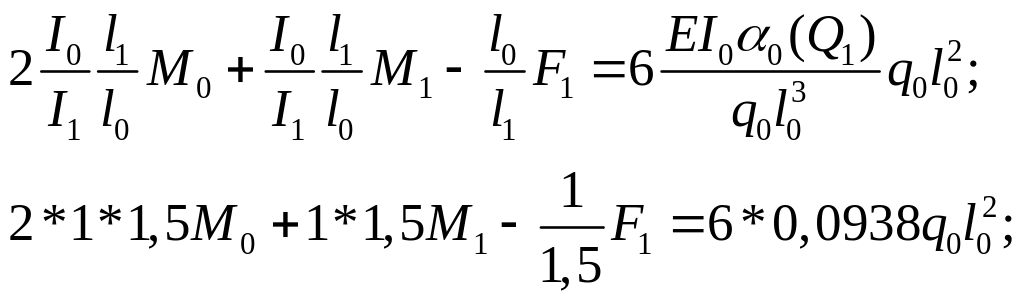
для опоры 1

для опоры2

где, с учетом соотношения (1.2),

Получаем систему уравнений

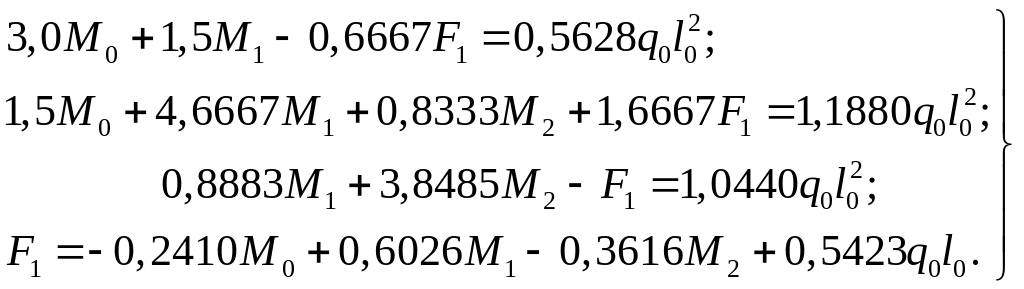
Исключая из первых трех уравнений F_1, приходим к системе уравнений для определения изгибающих моментов

(1.3)

Решение канонической системы уравнений (1.3) выполнено в табл. 1.2 по сокращенной схеме Гаусса [1, с.77].

Таблица 1.2

Решение системы уравнений (1.3)

Операции	Коэффициент при			Свободные члены при q0l02	Контроль
	M0	M1	M2
№ уравне- (1) ния систе- (2) мы (1.3) (3)	3,1607 1,0983 0,2410	1,0982 5,6711 0,2307	0,2411 0,2306 4,2101	0,9244 0,2841 1,5863	5,4244 7,2841 6,2681
I	-1	-0,3475	-0,0763	-0,2925	-1,7162
(4) = I*1,0983 (5) = (4) + (2)	-1,0983 -	-0,3816 5,2895	-0,0838 0,1468	-0,3212 - 0,0371	-1,8848 5,3992
II =	-	-1	-0,0278	0,0070	-1,0208
(6) = I*0,2411 (7) = II*0,1468 (8) =(6)+(7)+(3)	+ - -	+ + -	-0,0184 -0,0041 4,1876	-0,0705 0,0010 1,5168	-0,4138 -0,1499 5,7044
III= -(8) /4,1876 II I	- - 1	- 1 -	1 - -	0,3622 -0,0171 0,2708	1,3622 0,9829 1,2708
Проверка	0,8559	-0,0188	0,0873
	0,2974	-0,0970	0,0835
	0,0653	-0,0039	1,5250

В результате решения системы уравнений получены следующие значения моментов: M₀ = 0,2708q₀l₀² = 0,2708*20*2² = 21,7 кНм;

M₁= -0,0171q₀l₀² = -0,0171*20*2² = -1,4 кНм;

M₂= 0,3622q₀l₀² = 0,3622*20*2² = 29,0 кНм.

В последних трех строках табл.1.2 выполнена проверка результатов решения задачи путем подстановки полученных значений моментов в исходную систему уравнений (1.3). Сравнение величин левой и правой частей каждого уравнения произведено в столбце свободных членов. Погрешность вычислений определяется как отношение разности этих величин к сумме абсолютных величин результатов подстановки. Эта погрешность возникает в результате округления величин при «ручном» счете.

Погрешность вычислений первого уравнения составляет

второго

третьего

Построение эпюр изгибающих моментов и перерезывающих сил.

При построении эпюр изгибающих моментов и перерезывающих сил каждый пролет неразрезной балки рассматривается как однопролетная свободно опертая балка, находящаяся под воздействием заданной нагрузки и найденных опорных моментов. Затем эпюры для отдельных пролетов составляются в общую эпюру.

Определяем реакции опор.

В приведенных обозначениях реакций верхний индекс показывает номер опоры, нижний – пролета. Эпюры перерезывающих сил Ν и изгибающих моментов M приведены на рис. 1.4. Значения N и M в характерных точках балки отмечены на эпюрах циф рами.

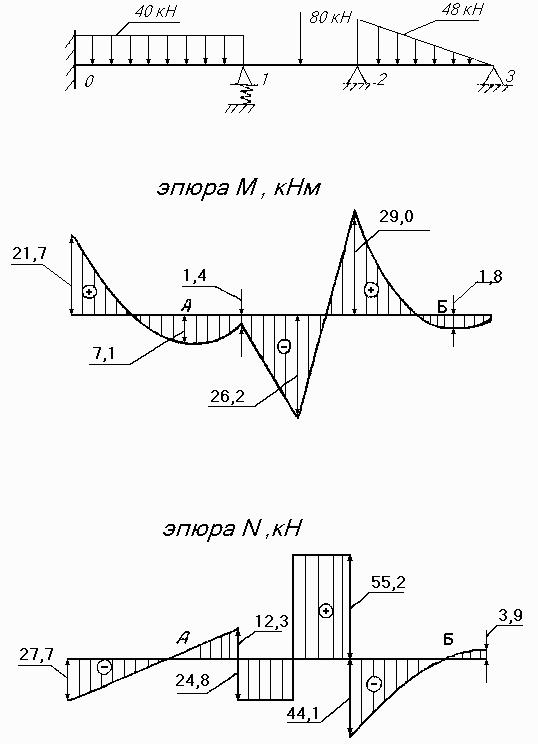
Рис.1.4. Эпюры изгибающих моментов и перерезывающих сил.

Отстояние точки А от левой опоры определяется из условия

, откуда

Отстояние x_1Б точки Б от правой опоры находим из соотношения

Изгибающие моменты в точках А и Б равны

Определение необходимых моментов сопротивления

поперечных сечений балок.

,

Нижние индексы при W обозначают пролет балки.

2.2. Задача 2. Расчет сложной рамы с неподвижными узлами.

2.2.1. Условия задачи 2.

Раскрыть статическую неопределимость сложной рамы с неподвижными узлами методом угловых деформаций. Построить эпюры изгибающих моментов и перерезывающих сил.

При решении задачи действующую на раму нагрузку разделить на две составляющие: симметричную и антисимметричную. Дальнейший расчет выполнять только для указанной в задании части нагрузки.

2.2.2. Методические указания к решению задачи 2.

Теоретические основы расчета сложных рам с неподвижными узлами содержатся в учебниках [ 2, с. 67-72 ], [ 3, c. 330-333 ] и справочнике [ 1, c. 308-310 ]. Эти же источники [ 2, c. 70 ], [ 1, c. 311 ] дают представление о разделении нагрузки на симметричную и антисимметричную части и об использовании условий симметрии конструкции в расчетах. Необходимо иметь в виду, что при симметричной нагрузке углы поворота узлов, расположенных на оси симметрии конструкции, равны нулю и в число неизвестных метода угловых перемещений не входит. Заметим, что в число неизвестных следует включать и углы поворота узлов i , содержащих лишь один свободно опертый конец стержня i – j. Для этих узлов также составляются уравнения их равновесия, т. е. M_ij=0.

Недостатком метода угловых деформаций является возможность появления разности близких величин при определении изгибающих моментов, что может привести к значительной погрешности при округлении чисел до малого количества значащих цифр. Поэтому следует обратить внимание на точность вычислений и после определения изгибающих моментов в узлах проверить выполнение условий их уравновешенности.

При построении эпюр изгибающих моментов и перерезывающих сил каждый стержень рамы рассматривается как свободно опертая балка, загруженная заданной нагрузкой и найденными узловыми моментами. Эпюры строятся в соответствии с принятым для балок правилом знаков, как например, при расчете неразрезных балок. При этом положительные моменты откладываются на растянутом волокне.

Следует помнить, что в методе угловых деформаций положительному значению момента M_ij соответствует его действие на балку со стороны узла против часовой стрелки.