Классификация термодинамических процессов

Процесс	Условия
Изотермический	Постоянная температура – T = const
Изобарный	Постоянное давление – p = const
Изохорный	Постоянный объем – V = const
Адиабатический	Отсутствие теплообмена между системой и внешней средой – Q=0

Первое начало термодинамики, или закон сохранения энергии, гласит, что энергия не может возникать из ничего и исчезать, а только переходит из одной формы в другую. Например, внутренняя энергия, содержащаяся в веществе, может превращаться в тепловую, световую (пламя), электрическую (химический аккумулятор) и т.д.

Например, сообщим системе некоторое количество тепловой энергии Q, которая расходуется на совершение работы A и на изменение состояния внутренней энергии системы U:

Q = A + U (7.1),

где U – изменение величины, которую называют внутренней энергией системы. Если система совершает работу за счет внутренней энергии без поступления теплоты, то A = –U (адиабатический процесс).

Таким образом, увеличению внутренней энергии системы соответствуют положительные значения U, уменьшению – отрицательные значения. Теплота, сообщаемая системе, и работа, совершаемая системой, также считаются положительными, и наоборот, теплота, отдаваемая системой, и работа, совершаемая над системой, считаются отрицательными.

Внутренняя энергия относится к функциям состояния, т.е. величинам, которые зависят только от состояния системы и не зависят от ее предыстории. Следовательно, изменение внутренней энергии в ходе процесса зависит только от начального и конечного состояния и не зависит от пути протекания процесса. Напротив, работа зависит от пути протекания процесса, и поэтому не обладает свойствами функции состояния, как «запас работы», которую может совершить система.

Единицей измерения работы, теплоты и внутренней энергии в системе СИ служит джоуль (Дж). 1 джоуль – это работа силы в 1 ньютон на расстоянии 1 м (1 Дж = 1 Нм = 1 кгм²/с²). В старой химической литературе широко использовалась единица количества теплоты и энергии калория (кал). 1 Калория – это такое количество теплоты, которое необходимо для нагревания 1 г воды на 1C. 1 Кал = 4,184 Дж  4,2 Дж. Теплоты химических реакций удобнее выражать в кило-джоулях или килокалориях: 1 кДж = 1000 Дж, 1 ккал = 1000 кал.

§ 3. Закон Гесса. В химической термодинамике первый закон трансформируется в закон Гесса, характеризующий тепловые эффекты химических реакций. Теплота, как и работа, не является функцией состояния. Поэтому для придания тепловому эффекту свойства функции состояния введена энтальпия (H), направленное изменение которой составляет H = U+PV при постоянном давлении. Отметим при этом, что PV = A – работе расширения, а H = –Q (с обратным знаком). Энтальпию характеризуют теплосодержанием системы так, что экзотермическая реакция понижает H. Обратите внимание, что выделению теплоты в химической реакции (экзотермической) соответствует H < 0, а поглощению (эндотермической) H > 0. В старой химической литературе была принята противоположная система знаков (!) (Q > 0 для экзотермических реакций и Q < 0 для эндотермических).

Изменение энтальпии (тепловой эффект) не зависит от пути реакции, а определяется только свойствами реагентов и продуктов (закон Гесса, 1836)

Покажем это на следующем примере:

C(графит) + O₂(г.) = CO₂(г.) H₁ = –393,5 кДж

С(графит) + ¹/₂ O₂(г.) = CO(г.) H₂ = –110,5 кДж

СО(г.) + ¹/₂ O₂(г.) = СО₂(г.) H₃ = –283,0 кДж

Здесь энтальпия образования CO₂ не зависит от того, протекает ли реакция в одну стадию или в две, с промежуточным образованием CO (H₁ = H₂ + H₃). Или иными словами сумма энтальпий химических реакций в цикле равна нулю:

rot (7.2),

где i – число реакций в замкнутом цикле.

В любом процессе, когда конечное и начальное состояния веществ одинаковы, сумма всех теплот реакции равна нулю.

Например, мы имеем последовательность из нескольких химических процессов, приводящих в конце к исходному веществу и характеризующихся каждый своей энтальпией, т.е.

(7.3)

то, согласно закону Гесса,

H₁ + H₂ + H₃ + H₄ = 0 (7.4)

Результирующий тепловой эффект равен нулю потому, что на одних стадиях тепло выделяется, на других – поглощается, что приводит к взаимной компенсации.

Закон Гесса позволяет вычислить тепловые эффекты тех реакций, для которых прямое измерение невозможно. Например, рассмотрим реакцию:

H₂(г.) + O₂(г.) = H₂O₂(ж.) H₁ = ?

Экспериментально легко измерить следующие тепловые эффекты:

H₂(г.) + ¹/₂O₂(г.) = H₂O(ж.) H₂ = –285,8 кДж

H₂O₂(ж.) = H₂O(ж.) + ¹/₂O₂(г.) H₃ = –98,2 кДж

Пользуясь этими значениями, можно получить:

H₁ = H₂ – H₃ = –285,8 + 98,2 = –187,6 (кДж/моль).

Таким образом, достаточно измерить тепловые эффекты ограниченного числа реакций, чтобы затем теоретически вычислить тепловой эффект любой реакции. На практике табулированы стандартные энтальпии образования H_f₂₉₈, измеренные при Т=298,15 К (25C) и давлении p = 101,325 кПа (1 атм), т.е. при стандартных условиях. (Не путать стандартные условия с нормальными!)

Стандартная энтальпия образования H_f – это изменение энтальпии в ходе реакции образования 1 моля вещества из простых веществ:

Ca (тв.) + C (графит) + ³/₂O₂ (г.) = CaCO₃ (тв.) H₂₉₈=–1207 кДж/моль.

Обратите внимание, что в термохимическом уравнении указываются агрегатные состояния веществ. Это очень важно, т.к. переходы между агрегатными состояниями (фазовые переходы) сопровождаются выделением или поглощением тепла:

H₂ (г.) + ¹/₂O₂ (г.) = H₂O (ж.) H₂₉₈ = –285,8 кДж/моль,

H₂ (г.) + ¹/₂O₂ (г.) = H₂O (г.) H₂₉₈ = –241,8 кДж/моль.

H₂O (г.) = H₂O (ж.) H₂₉₈ = –44,0 кДж/моль.

Стандартные энтальпии образования простых веществ приняты равными нулю. Если простое вещество может существовать в виде нескольких аллотропных модификаций, то H = 0 приписывается самой устойчивой при стандартных условиях форме, например, кислороду, а не озону, графиту, а не алмазу:

³/₂O₂ (г.) = O₃ (г.) H₂₉₈ = 142 кДж/моль,

C (графит) = C (алмаз) H₂₉₈ = 1,90 кДж/моль.

Следствием закона Гесса с учетом изложенного тогда изменение энтальпии в ходе реакции, будет равно сумме энтальпий образования продуктов за вычетом суммы энтальпий образования реагентов с учетом стехиометрических коэффициентов реакции:

H(реакции) = H_f(продуктов) – H_f(реагентов) (7.5)

Вычислим стандартную энтальпию реакции:

4Al (тв.) + 3PbO₂ (тв.) = 2Al₂O₃ (тв.) + 3Pb (тв.) (a)

Стандартные энтальпии образования найдем по справочным данным:

2Al (тв.) + ³/₂O₂ (г.) = Al₂O₃(тв.) H₂₉₈ = –1669,8 кДж/моль, (b)

Pb (тв.) + O₂ (г.) = PbO₂ (тв.) H₂₉₈ = –276,6 кДж/моль. (c)

С термохимическими уравнениями можно обращаться так же, как и с алгебраическими: умножать на число, складывать, вычитать, переносить слагаемые из одной части в другую.

4Al (тв.) + 3O₂ (г.) + 3Pb (тв.) + 3O₂ (г.) = 2Al₂O₃ (тв.) + 3PbO₂ (тв.)

H₂₉₈(a) = 2H₂₉₈(b) – 3H₂₉₈(c)

4Al (тв.) + 3PbO₂ (тв.) = 2Al₂O₃ (тв.) + 3Pb (тв.)

H₂₉₈(a) = 2(–1669,8)–3(–276,6) = –2509,8 кДж.

Обратите внимание, что свободный кислород, не участвующий в реакции, сократился при преобразованиях. На самом деле нет необходимости записывать расчеты так подробно. Если стехиометрические коэффициенты подобраны правильно, то баланс по всем веществам обязательно сойдется. Более кратко расчет H реакции записывают так:

4Al(тв.) + 3PbO₂(тв.) = 2Al₂O₃(тв.) + 3Pb(тв.)

ΔH_f₂₉₈ 0 3(–276,6) 2(–1669,8) 0

H₂₉₈ = 2(–1669,8)–3(–276,6) = –2509,8 кДж.

Цикл Борна – Габера. Важным развитием и следствием закона Гесса является установление взаимосвязи между термодинамическими параметрами реакции, химических соединений и энергетическими параметрами атома, молекулы (потенциал ионизации, энергия сродства к электрону, энергия хим. связи, кристаллической решетки и др.). Так, в «Практикуме по общей химии» и в других учебниках дан пример взаимосвязи потенциала ионизации атома натрия (I_Na), энергий диссоциации молекулы хлора (DH_дисс), сублимации (атомизации) натрия (H_ат), сродства к электрону (E_Cl), кристаллической решетки хлорида натрия (U) и собственно энтальпии образования хлорида натрия (H_обр). Так что можно записать

H_обр = H_ат + I_Na + H_дисс + E_Cl + U (7.6)

Ну, а вам останется только построить его графически еще раз.

Рассмотрим возможности цикла Борна – Габера на примере хлоридов (MeCl) и дихлоридов (MeCl₂) металлов. Величина U рассчитывается на основе закона Гесса (с использованием старых единиц – ккал).

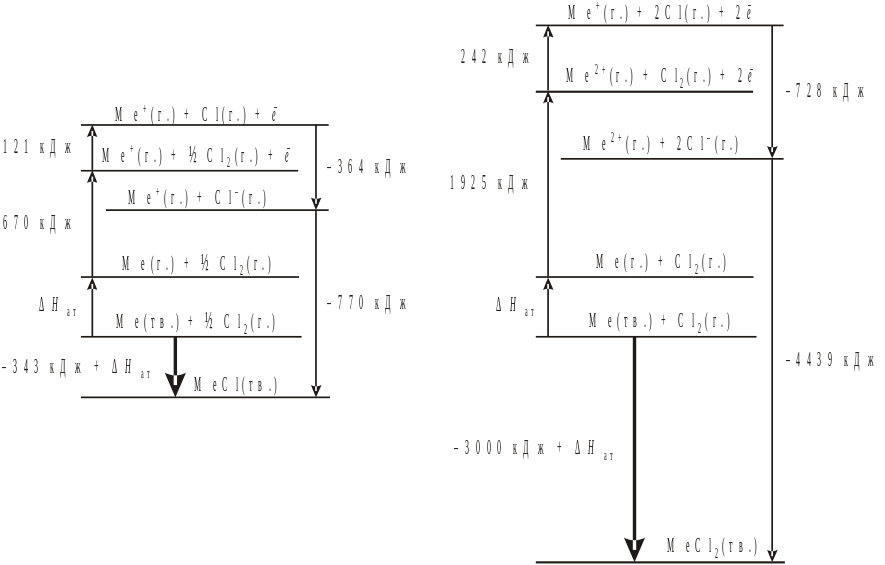
Какие же из хлоридов металлов более термодинамически устойчивы? В обоих случаях общей стадией является атомизация твердого металла с затратой неизвестного нам, но одинакового количества энергии H_ат. Очевидно, не эта величина определяет стабильность обоих хлоридов. Ионизация до двухвалентного состояния требует значительно большего количества энергии, чем однократная ионизация атома. На стадии ионизации хлора в случае MeCl₂ также требуется затратить вдвое больше энергии, чем для MeCl. Энергетически выгодна форма MeCl₂, а не MeCl. Хотя реакции 1-4 для MeCl и дают выигрыш 242 ккал/моль по сравнению с теми же реакциями для MeCl₂, это преимущество полностью теряется на стадии образования кристаллической решетки из ионов. Выигрыш за счет энергии решетки MeCl₂ оказывается 877 ккал/моль, что с избытком покрывает энергетические расходы на первых стадиях цикла. Поэтому, если даже соединение MeCl в какой-то момент возникает, то затем самопроизвольно по реакции диспропорционирования

2MeCl (тв.) = MeCl₂ (тв.) + Me (тв.)

переходит в дихлорид. Тепловой эффект такого процесса будет равен H = –553 – H_ат ккал/моль, т.е. очень большой величине, как раз и определяющей самопроизвольное течение реакции. Таким образом, можно без преувеличения сказать, что величина энергии кристаллической решетки определяет химическую или валентную форму ионного соединения.

Энергия кристаллической решетки в рядах однотипных соединений определяет также ряд свойств физико-химического характера, например температуру плавления и твердость.

Таблица 6.3.

Некоторые свойства галогенидов натрия.

	Энергия решетки, ккал/моль	Температура плавления, С	Твердость, ед. Мооса *
NaF	213	992	3,25
NaCl	186	800	2,5
NaBr	175	747	2,25
NaI	164	662	2,0

* За 10 принимается твердость алмаза, за 1 – твердость талька.

Видно, что U и свойства находится в прямой зависимости от радиуса иона. Вам остается графически построить оба цикла и по справочным данным оценить энергетические параметры для хлоридов магния, кальция, бария.

§ 4. Второе начало (второй закон) термодинамики. Энтропия. Выделение тепловой энергии в ходе реакции способствует тому, чтобы она протекала самопроизвольно, т.е. без постороннего вмешательства. Однако имеются и другие самопроизвольные процессы, при которых теплота равна нулю (например, расширение газа в пустоту) или даже поглощается (например, растворение нитрата аммония в воде). Это означает, что помимо энергетического фактора на возможность протекания процессов влияет какой-то другой фактор.

Он называется энтропийным фактором или изменением энтропии. Энтропия S является функцией состояния и определяется степенью беспорядка в системе. Опыт, в том числе повседневный, свидетельствует о том, что беспорядок возникает самопроизвольно, а чтобы привести что-нибудь в упорядоченное состояние, нужно затратить энергию. Это утверждение – одна из формулировок второго начала термодинамики.

Существуют и другие формулировки, например, такая: Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (Клаузиус, 1850). Брусок, нагретый с одного конца, со временем принимает одинаковую температуру по всей длине. Однако никогда не наблюдается обратный процесс – равномерно нагретый брусок самопроизвольно не становится более теплым с одного конца и более холодным с другого. Другими словами, процесс теплопроводности необратим. Чтобы отнять тепло у более холодного тела, нужно затратить энергию, например, бытовой холодильник расходует для этого электрическую энергию.

Рассмотрим сосуд, разделенный перегородкой на две части, заполненные различными газами. Если убрать перегородку, то газы перемешаются и никогда не разделятся самопроизвольно снова. Добавим каплю чернил в сосуд с водой. Чернила распределятся по всему объему воды и никогда не соберутся самопроизвольно в одну каплю. В обоих случаях самопроизвольно протекающие процессы сопровождаются увеличением беспорядка, т.е. возрастанием энтропии (S > 0). Если мы рассматриваем изолированную систему, внутренняя энергия которой измениться не может, то самопроизвольность процесса в ней определяется только изменением энтропии: В изолированной системе самопроизвольно идут только процессы, сопровождающиеся возрастанием энтропии (Больцман, 1896). Это также одна из формулировок второго начала термодинамики. Наглядно проявление энтропийного фактора можно увидеть в фазовых переходах лед–вода, вода–пар, протекающие при постоянной температуре. Как известно при этом происходит поглощение (ледоход – похолодание) и выделение тепла (ледостав – потепление) так, что

H_Г = ST (7.7),

где H_Г – «скрытая» теплота фазового перехода. В фазовых переходах лед–вода–пар – S_л < S_в < S_п, т.е. энтропия возрастает при переходе от твердого тела к жидкости и от жидкости к газу, а ее величина тем больше, чем беспорядочнее движутся молекулы. Таким образом, энтропия отражает структурные отличия одного и того же химического элемента, молекулы, вещества. Например, для той же воды H₂O – кристалл, жидкость, пар; для углерода – графит, алмаз, как аллотропные модификации и т.д.

Абсолютное значение энтропии можно оценить с использованием третьего начала термодинамики (постулата Планка), которое утверждает, что энтропия идеального кристалла при 0 К равна нулю lim S=0 (при T0).

Единицей измерения энтропии в системе СИ является Дж/Кмоль. При этом понятно, что абсолютный нуль температуры недостижим (следствие из второго закона термодинамики), но он имеет важное значение в определении температуры – шкалы Кельвина.

Кроме того, есть еще одна функция состояния вещества – теплоемкость

С = H/T, (7.8)

которая имеет такую же размерность, что и энтропия, но означает способность того или иного вещества отдавать (принимать) тепло при изменении температуры. Например, при изменении температуры на 100°С сталь быстрее нагреется и остывает соответственно, чем кирпич, поэтому печки кладут из кирпича. Величины теплоемкости удельные или молярные табулированы в справочниках обычно для изобарных условий – c_p.

Стандартные абсолютные энтропии S₂₉₈ образования некоторых веществ приведены в справочной литературе. Обратите внимание, что в отличии от H_f простые вещества имеют значения S₂₉₈ > 0, т.к. их атомы и молекулы также находятся в беспорядочном тепловом движении. Чтобы найти изменение энтропии в реакции, можно также применить следствие закона Гесса:

S(реакции) = S(продуктов) – S(реагентов) (7.9)

S > 0 согласно второму началу термодинамики благоприятствует протеканию реакции, S < 0 — препятствует.

Качественно можно оценить знак S реакции по агрегатным состояниям реагентов и продуктов. S > 0 для плавления твердых тел и испарения жидкостей, растворения кристаллов, расширения газов, химических реакций, приводящих к увеличению числа молекул, особенно молекул в газообразном состоянии. S < 0 для сжатия и конденсации газов, затвердевания жидкостей, реакций, сопровождающихся уменьшением числа молекул.

Пользуясь справочными данными , рассчитаем S₂₉₈ реакции (а).

4Al (тв.) + 3PbO₂ (тв.) = 2Al₂O₃ (тв.) + 3Pb (тв.)

S₂₉₈ 428,32 376,6 250,99 364,89

S₂₉₈ = 250,99+364,89–428,32–376,6 = –46,4 Дж/К.

Таким образом, энтропийный фактор препятствует протеканию этой реакции, а энергетический фактор (см. выше) – благоприятствует.

Идет ли реакция на самом деле? Чтобы ответить на этот вопрос, нужно одновременно рассмотреть оба фактора: энтальпийный и энтропийный.

§ 5. Свободная энергия Гиббса. Критерии самопроизвольности протекания химических реакций. Одновременный учет энергетического и энтропийного факторов приводит к понятию еще одной полной функции состояния – свободной энергии. Если измерения проводятся при постоянном давлении, то величина называется свободной энергией Гиббса (в старой химической литературе – изобарно-изотермическим потенциалом) и обозначается G.

Свободная энергия Гиббса связана с энтальпией и энтропией соотношением:

G = H – TS (7.10)

где T – температура в кельвинах. Изменение свободной энергии Гиббса в ходе реакции образования 1 моля вещества из простых веществ в стандартных состояниях называется свободной энергией образования ΔG и обычно выражается в кДж/моль. Свободные энергии образования простых веществ приняты равными нулю. Чтобы найти изменение свободной энергии Гиббса в ходе реакции, нужно от суммы свободных энергий образования продуктов отнять сумму свободных энергий образования реагентов с учетом стехиометрических коэффициентов:

G(реакции) = G(продуктов) – G(реагентов) (7.11)

Самопроизвольным реакциям соответствует G < 0. Если G > 0, то реакция при данных условиях невозможна. Рассмотрим реакцию (a)

4Al (тв.) + 3PbO₂ (тв.) = 2Al₂O₃ (тв.) + 3Pb (тв.)

ΔG₂₉₈ 0 3(–219,0) 2(–1576,5) 0

ΔG₂₉₈ = 2(–1576,5)–3(–219,0) = –2496 кДж.

Существует и другой способ расчета G реакции. Выше мы нашли значения ΔH и ΔS, тогда G = H – TS

G₂₉₈ = –2509,8 кДж – 298,15 К(–0,0464 кДж/К) = –2496 кДж.

Таким образом, реакция (1) при стандартных условиях протекает самопроизвольно. Знак ΔG показывает возможность осуществления реакции только в условиях, для которых проводились вычисления. Для более глубокого анализа необходимо раздельное рассмотрение энергетического и энтропийного факторов. Имеется четыре возможных случая:

Таблица 7.3.

Определение возможности протекания химической реакции

Критерии	Возможность
H < 0, S > 0	Оба фактора благоприятствуют реакции. Как правило, такие реакции протекают быстро и полностью.
H < 0, S < 0	Энергетический фактор благоприятствует реакции, энтропийный препятствует. Реакция возможна при низких температурах.
H > 0, S > 0	Энергетический фактор препятствует реакции, энтропийный благоприятствует. Реакция возможна при высоких температурах.
H > 0, S < 0	Оба фактора препятствуют реакции. Такая реакция невозможна.

Если при стандартных условиях G реакции > 0, но энергетический и энтропийный факторы направлены противоположно, то можно рассчитать, при каких условиях реакция станет возможной. H и S химической реакции сами по себе слабо зависят от температуры, если какие-нибудь из реагентов или продуктов не испытывают фазовых переходов. Однако в энтропийный фактор помимо S входит также и абсолютная температура T. Таким образом, с повышением температуры роль энтропийного фактора повышается, и при температуре выше T  H/S реакция начинает идти в обратном направлении.

Если G = 0, то система находится в состоянии термодинамического равновесия, т.е. G – термодинамический критерий химического равновесия реакций (смотри вышеприведенные фазовые переходы воды).

Итак, анализируя функции состояния системы – энтальпию, энтропию и свободную энергию Гиббса – и их изменение в ходе химической реакции, можно определить, будет ли данная реакция происходить самопроизвольно, и тем самым ответить на вопросы, поставленные в начале этой лекции.

Более полно термодинамика отражена в курсе физической химии, а с прикладными ее аспектами вы ознакомитесь в курсах теплотехники и др.