2.3 Розрахункова робота № 3 ”Дисперсійний аналіз”

Мета роботи

Набути практичні навички проведення дисперсійного аналізу.

Програма роботи

1. Виявити наявності (відсутність) зв’язку між ознаками та встановити його характер.

2. Перевірити істотность зв’язку за допомогою критеріїв математичної статистики.

Основні теоретичні положення

Дисперсійний аналіз грунтується на правилі декомпозиції( складанні) дисперсій: загальна дисперсія складається з міжгрупової та середної з групових дисперсій. Загальна дисперсія характеризує варіацію результативної ознаки, під впливом всіх факторів, що на неї впливають. Групові дисперсії та середня з групових дисперсій характеризують варіацію результативної ознаки, пов’язану з варіацією всіх факторних ознак, крім тієї, яка покладена в основу групування. Міжгрупова дисперсія характеризує варіацію результативної ознаки, яка пов’язана з варіацією групувальної ознаки.

Корень квадратний відношення міжгрупової дисперсії до загальної характеризує тісноту кореляційного зв’язку і тому його називають кореляційним.

Порядок виконання роботи

Вихідні дані ( значення факторної і результативної ознак), а також допоміжні розрахунки заносять в таблицю 2.6.

1 Обчислюють загальну середню за формулою: а також міжгрупову та внутрішньогрупову девіаці за формулами, відповідно: ,

Таблиця 2.6

Групи за факторною ознакою х	Варіанти результативної ознаки у	Суми варіант ∑y¡	Групові середні	Відхилення груп. середніх від заг. серед-ньої	Квадрат відхилень	Відхи-лення варіант від груп. середніх	Квадрат відхи-лень
Суми, середня девіація	n	∑y		-		-

2 Обчислити загальну девіацію відповідно до правила додавання девіацій загальна девіація розраховується за формулою

,

3 Обчислити коефіцієнт детермінації. Коефіцієнт детермінації обчислюють за формулою:

,

Дати економічну інтерпретацію одержаного значення.

4 Визначити емпіричне кореляційне відношення за формулою:

.

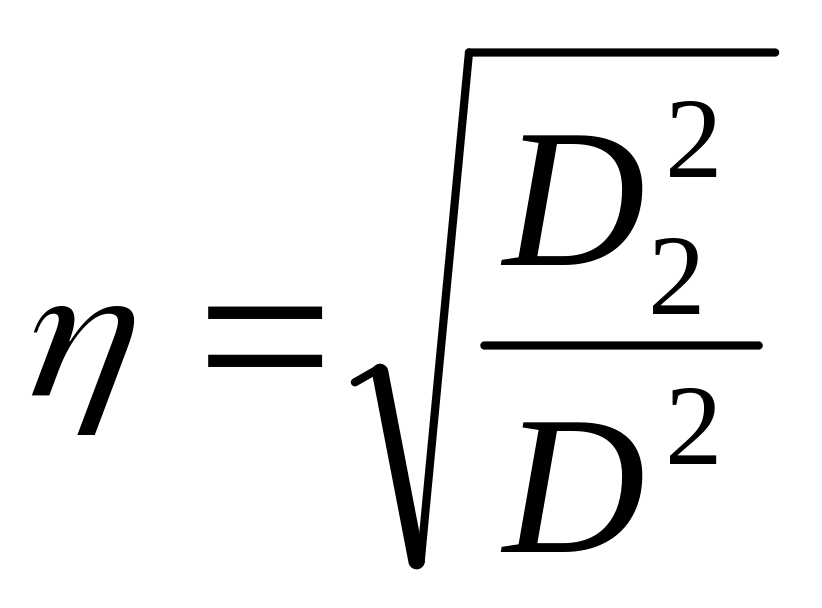Зробити висновок про наявність (відсутність) зв’язку між факторною та результативною ознаками та про його характер (кореляційний або функціональний).

5 Перевірити істотність кореляційного зв’язку при допомозі F – критерію Фішера. F – критерій Фішера обчислюють за формулами:

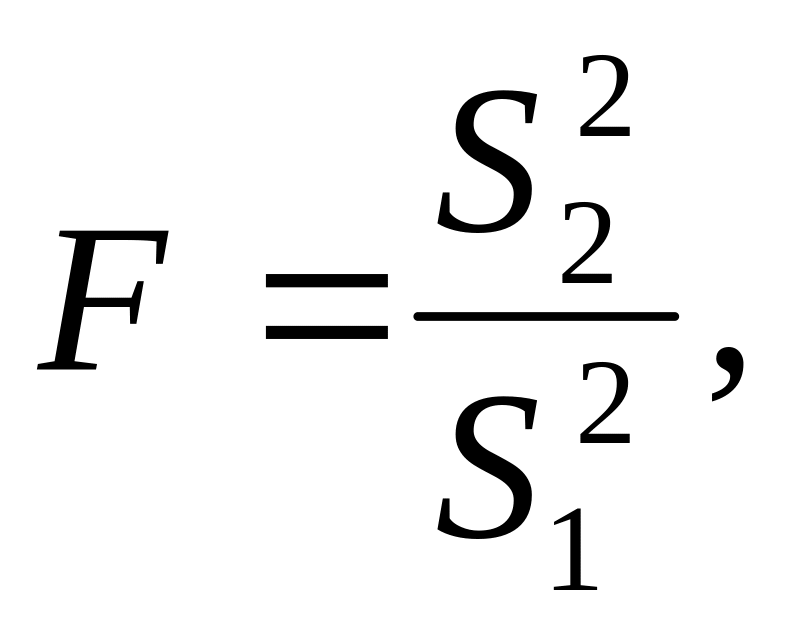якщо або

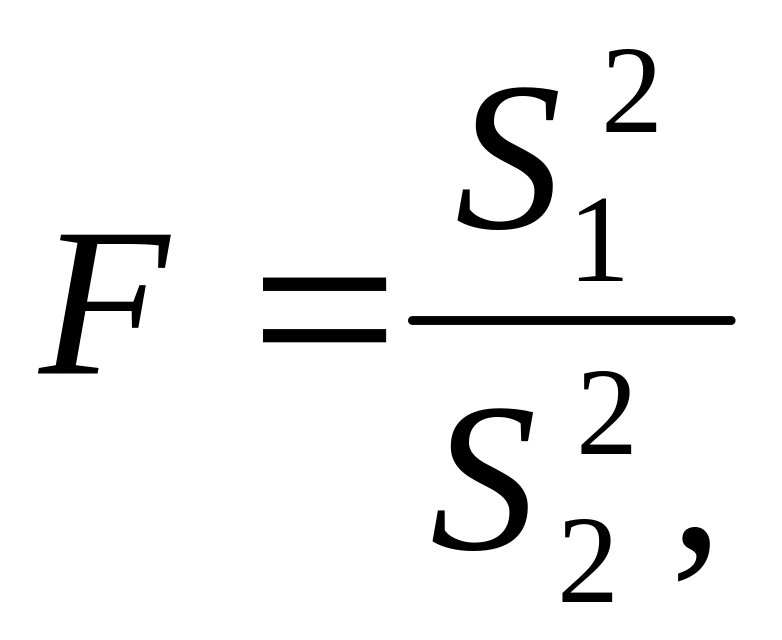, якщо

де - оцінювальні дисперсії, які обчислюють за формулами:

,

.

де n - чисельність одиниць сукупності;

m - число груп, утворених за факторною ознакою.

6 З імовірностями 0.95 та 0.99 і за ступенями вільності (n-m) та (m-1) знайти критичні значення F – критерію Фішера і порівнятиь їх з фактичним значенням. Зробити висновок про достовірність кореляційного зв’язку між факторною та результативною ознаками.