3 Оцінка істотності відхилень емпіричних і теоретичних частот.

Для оцінки близькісті емпіричних і теоретичних частот,(чи є випадковими розходження між ними) використовують критерії узгодження.

Критерій Пірсона обчислюють за формулою:

Вихідні та розрахункові значення заносяться в таблицю 2.4

Таблиця 2.4 – Розрахунок критерію Пірсона

Частоти		Відхилення f-f´	(f-f´)²
f	f´

Значення   χ2   табульовані для ймовірності 1 - та числа ступенів волі k = m–r-1, де m – число груп,

r- число параметрів( для нормальної кривої r=2( )). Порівнюють розрахункове і табличне значення критерію і роблять висновок про істотність відхилень між емперічними і теоретичними частотами.

Критерій Колмогорова обчислюють за формулою:

,

де - число спостережень, або загальна чисельність варіант;

- нагромаджені емпіричні і теоретичні частоти;

- максимальна величина розходжень між нагромадженими частотами.

Вихідні та розрахункові значення заносяться в таблицю 2.5

Таблиця 2.5 – Розрахунок критерію Колмагорова

Частоти		Нагромаджені частоти		S-S´
f	f´	S	S´

Імовірність того, що λ досягає обчисленої величини, знаходять в стандартних таблицях значень Р(λ).

На підставі одержаних результатів роблять висновок, чи відхилення між емпіричними і теоретичними частотами має випадковий характер, чи воно є наслідком невідповідності теоретичної кривої розподілу реальному характеру розподілу.[1]

Критерій згоди Романовського

Для розрахунку критерію Романовського використовуються також величини χ2 та k :

R = , якщо R<3 можна стверджувати, що розподіл частот підлягає нормальному закону .

Критерій згоди Ястремського використовують для безпосередньої відповіді на запитання про міру розбіжності між фактичним і теоретичним розподілом.

L = ,

де n – кількість груп; χ² – критерій Пірсона;

де

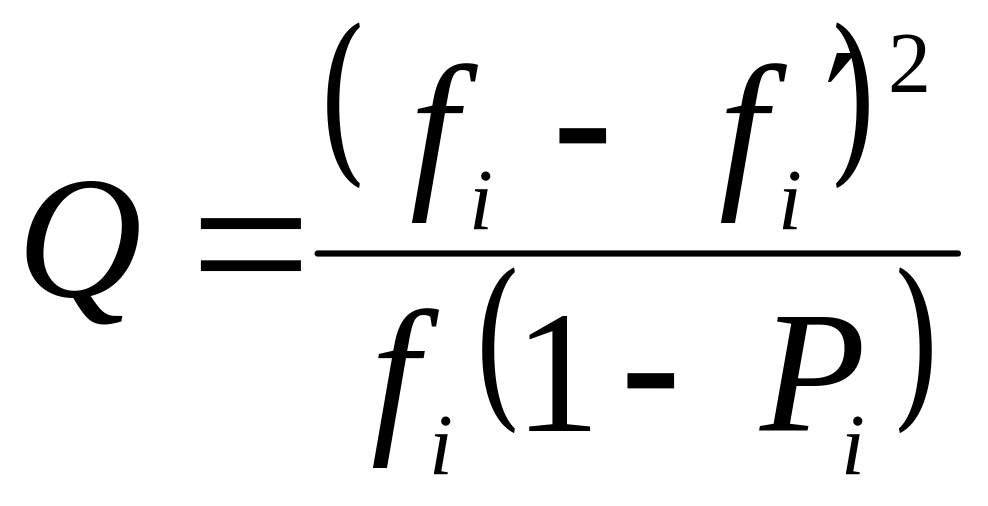
Q – Приймає значення 0,6, якщо кількість груп n < 20.

Якщо підтверджується гіпотеза про нормальний розподіл, будують емпіричні та теоретичні криві розподілу.

3 Обчислення показників асиметрії і ексцесу.

Якщо відхилення між емпіричними і теоретичними частотами носять істотний характер, то аналіз розподілу розширюють характеристиками асиметрії і ексцесу.

Коефіцієнт асиметрії обчислюють за формулою:

,

де - центральний момент третього порядку.

Коефіцієнт ексцесу обчислюють за формулою:

,

де -центральний момент четвертого порядку.

За даними інтервального ряду розподілу розрахунок центральних моментів та можна розрахувати скориставшись властивостями середніх величин за формулами:

,

,

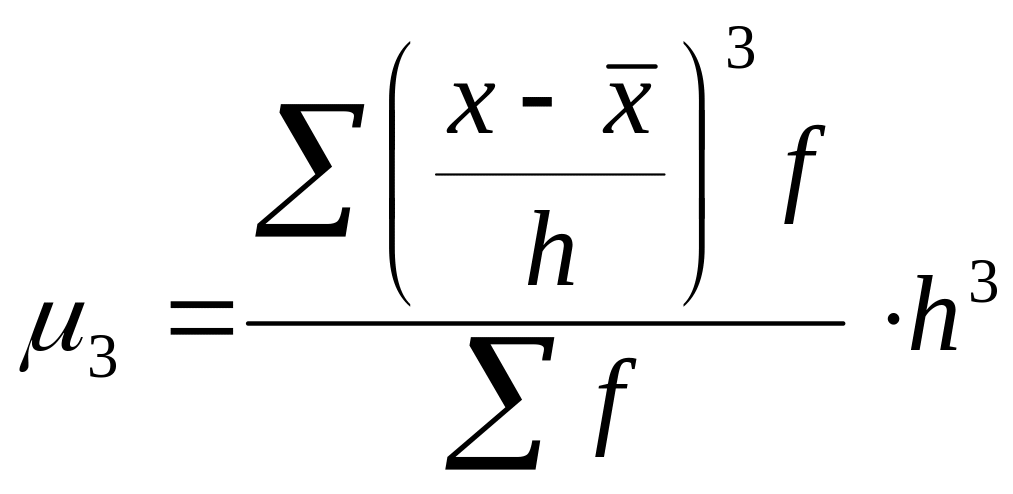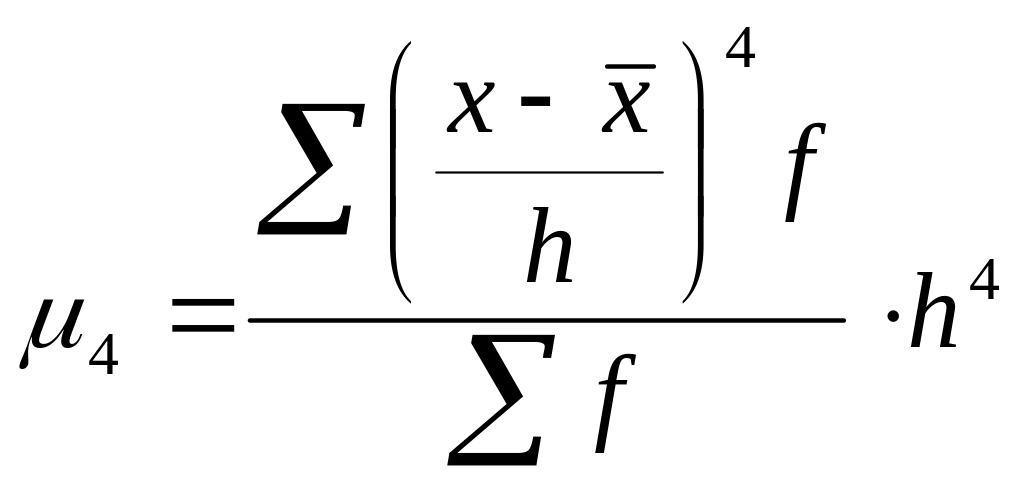де h - ширина (множник h може бути будь-яким числом);

- частота або частка інтервалу.

За допомогою середньої квадратичної похибки асиметрії і середньої квадратичної похибки ексцесу встановлюється істотність кожного з цих показників для розподілу ознаки в генеральній сукупності. Якщо :

>3,

де , то асиметрія істотна і розподіл ознаки в генеральній сукупності несиметричний.( n- кількість одиниць сукупності).

Якщо виконується умова :

, то ексцес є властивим для генеральної сукупності.

При виконанні роботи можна використовувати програми Excel 5 або Excel 7.

Обробка результатів

Після обчислення та аналізу показників центру розподілу та варіації роблять висновок про закон розподілу ознаки, визначають ступінь асиметрії та роблять висновок про форму розподілу ( гостровершиний чи плосковершиний) ..

Контрольні запитання

1. Що характеризують середня арифметична, мода і медіана?

2. Що таке мода, дайте визначення ?

3. За яким показником визначається однорідність сукупності ?

4. Де використовуються теоретичні криві розподілу?

5. Що таке нормальний розподіл і його властивості ?