6. Контральные вопросы.

1. В каких случаях применяется основное уравнение гидростатики и закон Паскаля?

2. Дайте определение абсолютного, манометрического, вакуумметрического давления.

3. Каков теоретический предел вакуума?

4. Какое давление будет в четвертом сечении трубы, если показания пьезометрической трубки h=0?

ЛАБОРАТОРНАЯ РАБОТА №3

ОПЫТНАЯ ДЕМОНСТРАЦИЯ УРАВНЕНИЯ БЕРНУЛЛИ.

1. Цель работы

Экспериментальное исследование закона сохранения энергии (уравнение Бернулли) для потока реальной несжимаемой жидкости в трубе переменного сечения.

2. Уравнение бернулли.

Уравнение Бернулли выражает закон сохранения энергии для потока жидкости. Для любых двух сечений (1-1 и 2-2 на рис.3.1) элементарной струйки реальной несжимаемой жидкости (например, на оси потока) уравнение Бернулли имеет вид

(3.1)

Р ис. 3.1. Схема рабочего участка гидростенда.

где gz – удельная энергия положения;

z₁, z₂ – геометрическая высота, измеряемая от плоскости сравнения до элементарной струйки;

- удельная энергия давления;

р₁, р₂ – гидростатическое давление в данной точке;

- удельная кинетическая энергия;

 – скорость потока элементарной струйки в олределенном сечении;

gh_w – удельная суммарная потеря энергия на преодоление сопротивлений между сечениями 1 и 2.

Уравнение (3.1) можно представить в виде

,

где Е – полная удельная энергия потока в данном сечении.

Зная Е₁ и Е₂, можно определить потерю энергии, затрачиваемую на преодоление сопротивлений между сечениями 1-1 и 2-2:

, (3.2)

При движении жидкости в трубе её энергия теряется на преодоление сопротивления трения по длине и на местные сопротивления

, (3.3)

где gh_mр – потеря удельной энергии на трение по длине;

gh_м – потеря удельной энергии на местных сопротивлениях.

Так как в реальной жидкости при её движении всегда имеют место потери энергии, то

Е₁>Е₂>Е₃>…>Е_n

Если все члены уравнения (3.1) разделить на ускорение свободного падения g, то получим уравнение Бернулли в форме напоров

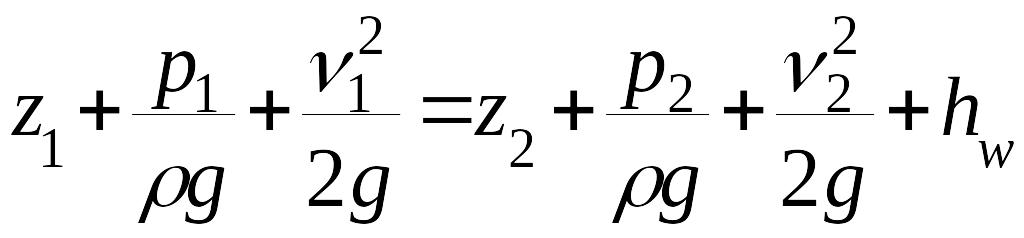, (3.4)

в котором размерность всех членов – линейная.

Уравнение (3.4) можно представить в виде

H₁=H₂+h_w, (3.5)

где Н – полный напор в данном сечении.

Уравнение Бернулли в форме напоров удобно применять для изучения закономерностей изменения удельной энергии потока жидкости по длине трубы.

3. Программа работы.

1. Определить напор Н в трех точках на оси трубы, найти потери напора.

2. Определить скорость потока на оси трубы.

3. Построить графики изменения полного напора Н и гидростатического 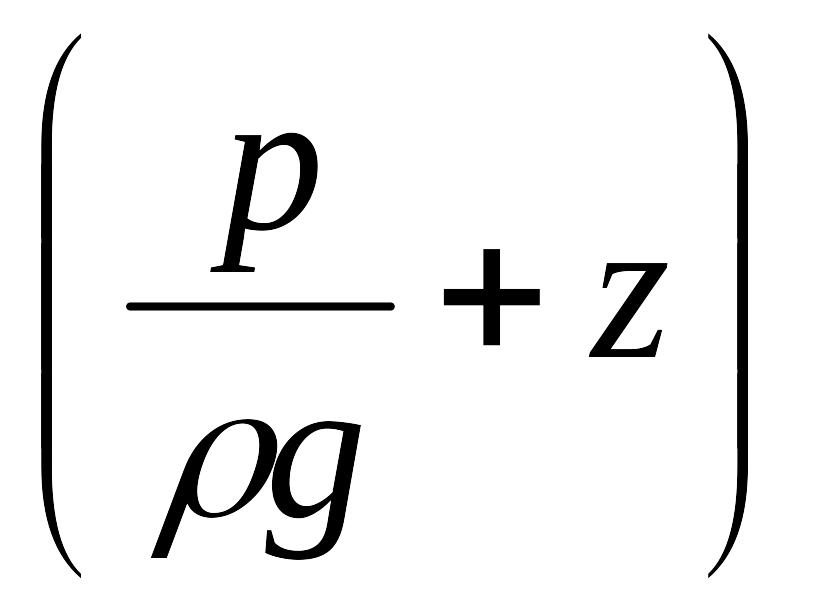напора по длине трубы.

4. Описание установки.

Рабочий участок гидростенда (см. описание гидростенда ГС-3) для данной лабораторной работы представляет собой трубу переменного сечения (рис.3.1). Для измерения статического и полного давлений жидкости в сечениях 1-1, 2-2 и 3-3 установлены пьезометрические трубки и трубки Пито.

Регулирование расхода жидкости в трубе производится вентилем 8 и 18, причем давление в расходном баке, измеряемое образцовым манометром 1, не должно превышать 20 делений манометра.