3. Индивідуальне розрахунково-графічне завдання

3.1. Пояснення для вирішення завдання

3.1.1. Розрахунок константи рівноваги хімічної реакції

В основі розрахунку константи рівноваги хімічної реакції:

аА + bB = cC + dD, (3.1)

де a, b, c, d – стехіометричні коефіцієнти; А, B – вихідні компоненти; C, D – продукти реакції (всі речовини в системі газоподібні), полягає рівняння стандартної хімічної спорідненості:

, (3.2)

де - стандартна зміна енергії Гіббса системи в результаті хімічної реакції; - стандартна константа рівноваги:

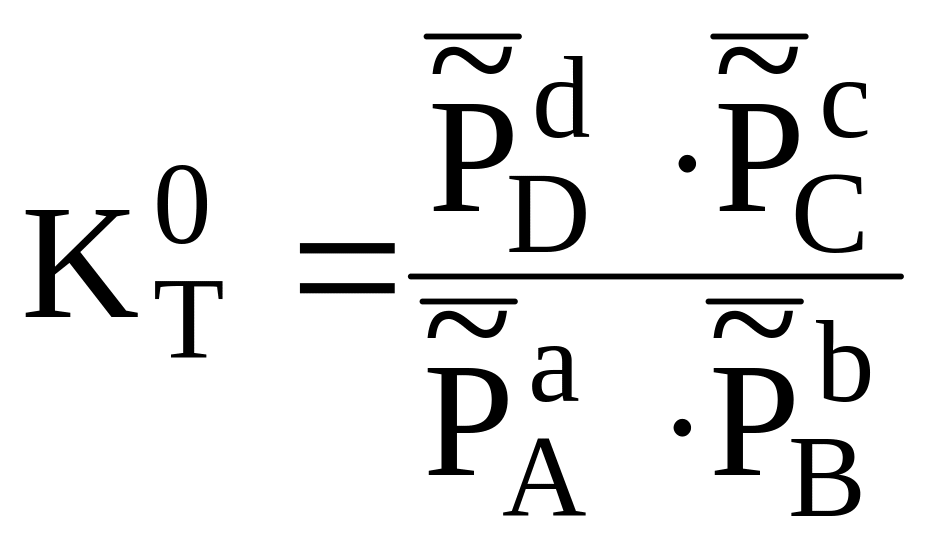, (3.3)

де - приведений рівноважний тиск, який визначається через парціальний рівноважний тиск ( ) відносно стандартного тиску (Р⁰): .

Зміну вільної енергії знаходять за рівнянням Гіббса-Гельмгольца:

. (3.4)

Для цього необхідно знати теплоту реакції при довільній температурі та зміну ентропії .

можна розрахувати за рівнянням Кірхгофа:

(3.5)

- за рівнянням:

. (3.6)

В цих рівняннях , - стандартні ентальпія та ентропія реакції при Т = 298 К, їх розраховують із співвідношень:

. (3.7)

. (3.8)

(теплота утворення) і (абсолютна ентропія) є властивостями даних речовин та приведені в довіднику; ν_i – стехіометричні коефіцієнти продуктів реакції і вихідних речовин; ΔC_p - зміна теплоємності в ході реакції, яка розраховується за рівнянням:

. (3.9)

Теплоємність є функцією від температури, яка виражається у вигляді степеневих рядів:

(органічні речовини) (3.10)

(неорганічні речовини)

(коефіцієнти а, b с, с´ приведені в довіднику [6]). Враховуючи ці залежності, можна записати:

, (3.11)

де Δа розраховується як:

. (3.12)

Інші коефіцієнти (Δb, Δс, Δс´), що залежать тільки від природи реагуючих речовин, розраховуються аналогічно.

Відповідно з вищезазначеним:

, (3.13)

де М₀, М₁, М₂, М_-2 - функції, що залежать тільки від температури.

Рівняння (3.13) має назву Тьомкіна-Шварцмана. Для температур кратних 100, значення величин М приведені в довідниках.

Для інших температур ці функції розраховуються за рівняннями:

, (3.14)

, (3.15)

де n – відповідає індексу при М (крім n = 0).

Таким чином, стандартну константу рівноваги можна вирахувати за рівнянням: . (3.16)

3.2. Розрахунки виходу продуктів реакції

Для розрахунку виходу продуктів реакції необхідно знати чисельний вираз термодинамічної константи рівноваги , константи рівноваги, що виражена через рівноважне число молей реагуючих речовин , загальний тиск Р, зміну числа молей реагуючих газоподібних речовин в ході реакції Δn та суму числа молей в рівноважному стані Σn:

. (3.17)

Розглянемо приклад рівнянь для розрахунків , Σn та Δn коли початковий вміст вихідних речовин чисельно дорівнює стехіометричним коефіцієнтам, а через х позначається доля перетворення речовини до моменту досягнення рівноваги.

Реакція:	аА	+	bB	=	cC	+	dD
Вихідний вміст речовин (t=0)	а		b		-		-
До моменту встановлення рівноваги прореагувало та утворилось	ax		bx		cx		dx
Рівноважний вміст	a(1-x)		b(1-x)		cx		dx

Підставив у вираз для константи рівноваги K_n число молей кожної речовини, що складають рівноважну суміш, отримаємо:

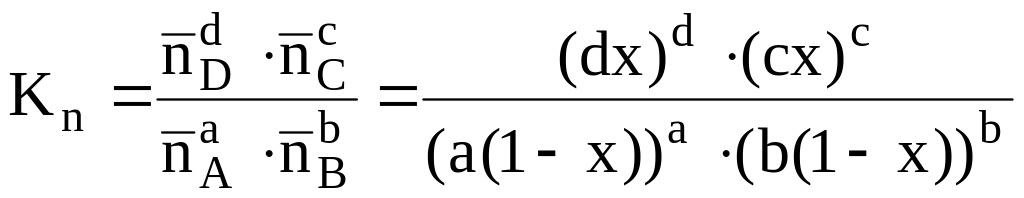(3.18)

де - рівноважний вміст і-го компоненту: x – доля перетворення речовини;

Σn = a(1-x) + b(1-x) + cx + dx; (3.19)

Δn = c + d – a - b (3.20)

Якщо рівняння (3.18) має ступінь вищий за другу, доля х речовини, що прореагувала до моменту рівноваги, розраховується одним з ітераційних методів. Тут використовується метод половинного ділення, який полягає в тому, що при кожній ітерації 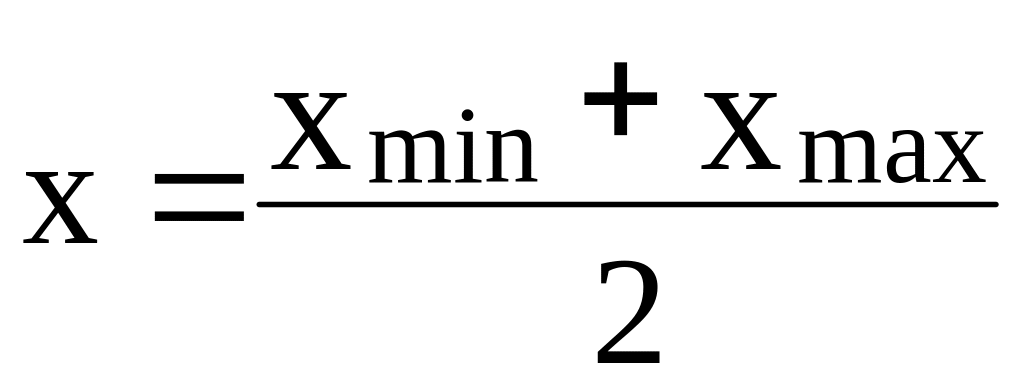(х_min та x_max– межі пошуку виходу x продукту). При цьому, якщо f(x) < , то x_min присвоюється значення x, якщо , то x_max → x .

Пошук значення x, що задовольняє нерівності

ε, (3.21)

де ε – межа мінімізації, f(x) - права частина рівняння (3.17), що відбувається в інтервалі . При цьому збіжність ряду визначається за нерівністю:

, (3.22)

де x_min та x_max – відповідно верхня та нижня межа інтервалу пошуку; Δ - задана погрішність розрахунку, що приймається звичайно 0,01 (1%). Початкові межі пошуку: x_min = 0, x_max = 1.