3. Приклад розв’язання завдання

Умова завдання. В таблиці 2.4 наведені дані по залежності тиску насиченої пари від температури, густини речовини в твердому і рідкому станах (d_тв і d_рід в кг/м³) в потрійній точці. Таблиця 2.4

Стан твердий		Стан рідкий		Умови
Т,К	р, Па	Т,К	р, Па
437,7 441,2 444,2 448,2	35324 39323 42659 47454	446,4 448,2 451,2 460 470	47000 47454 49563 55986 63317	М = 152 Р = 300.105 Па dтв = 985 dрід = 977

Задача 1. Побудуйте графік залежності ln p від 1/Т.

Розв’язання. Для креслення графіка перерахуємо р на ln р, а Т на 1/Т. Дані занесемо в таблицю 2.5. Через точки, що характеризують твердий стан і через точки рідкого стану проводимо дві прямі лінії (рис. 1).

Таблиця 2.5

Стан
твердий		рідкий
1/Т.103	ln p	1/Т.103	ln p
2,285 2,267 2,251 2,231	10,4723 10,5796 10,6610 10,7675	2,240 2,231 2,216 2,174 2,128	10,7580 10,7675 10,8110 10,9329 11,0559

Задача 2. Визначить за графіком координати потрійної точки.

Розв’язання.. Точка перетину побудованих прямих є потрійна точка (т. о). Її координати: ln p = 10,7675 і 1/Т = 2,251^.10^-3, що відповідає тиску р_ПТ = 47454 Па і температурі Т_ПТ =448,2 К.

Задача 3. Обчисліть середню теплоту випаровування і сублімації.

Рис. 1.

Розв’язання. Лінія со є лінією випаровування. Її хід описується рівнянням Клапейрона-Клаузіуса у лінійному вигляді:

.

Аналіз рівняння показує, що теплота випаровування входить в величину кутового коефіцієнта прямої. Він дорівнює тангенсу кута нахилу лінії (α₁), який можна розрахувати за графічними даними:

.

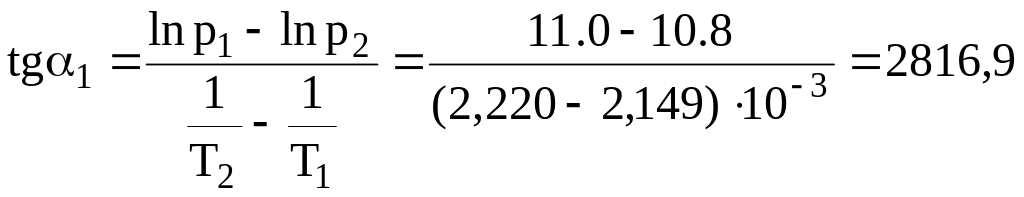Середня теплота випаровування дорівнює:

ΔH_ВИП = R^.tgα₁ = 8,314^. 2816,9 = 23429,7 Дж/моль.

Лінія оb на графіку є лінією сублімації. Вона також описується рівнянням Клапейрона-Клаузіуса. Тангенс кута нахилу (α₂) прямої оb дорівнює:

.

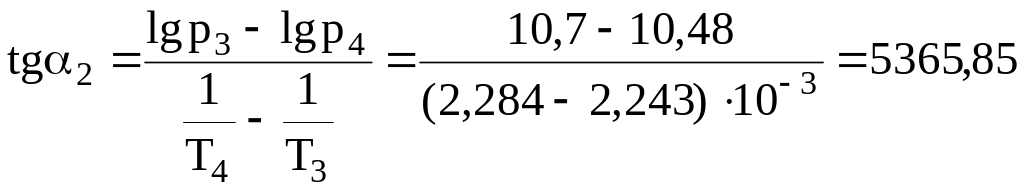Розрахуємо середню теплоту сублімації.

ΔH_СУБ = R^.tgα₂ = 8,314^. 5365б85 = 44611,7 Дж/моль.

Задача 4. Визначить теплоту плавлення речовини при температурі потрійної точки.

Розв’язання. Теплоту плавлення речовини при температурі потрійної точки визначаємо за рівнянням:

ΔH_ПЛ = ΔH_СУБ. – ΔH_ВИП = 44611,7 - 23419,7 – 21192,0 Дж/моль.

Задача 5. Обчисліть dT/dp для процесу плавлення при температурі потрійної точки.

Розв’язання. Згідно з рівнянням Клапейрона – Клаузіуса

,

де ΔV = V_РІД – V_ТВ є різниця мольних об’ємів речовини в рідкому і твердому станах відповідно. Мольні об’єми розрахуємо за даними густини речовини (d_РІД і d_ТВ) та її мольної маси (М = 152 г/моль)

і .

Тоді

,

і .

Задача 6. Обчисліть температуру плавлення речовини при тиску р.

Розв’язання. Температуру плавлення при тиску 300^.10⁵ Па знайдемо в результаті інтегрування рівняння

,

допускаючи, що залежність T = f(p) має лінійний характер.

.

Т = Т_ПТ + 2,67^.10^-8(р – р_ПТ) = 448,2 + 2,67^.10^-8(300^.10⁵ – 47454) = 449,0 К.

Задача 7. Обчисліть зміну ентропії, ентальпії, внутрішньої енергії, енергії Гіббса, енергії Гельмгольца в процесі сублімації для n = 1 кмоль речовини в потрійної точці.

Розв’язання. Для процесу сублімації в потрійній точці зміна ентропії 1 кмоль речовини дорівнює:

.

Зміна ентальпії буде дорівнювати:

ΔН = nΔН_СУБ = 1000^.44611,7 = 44611700 Дж.

Зміна внутрішньої енергії:

ΔU = ΔH – nRT_ПТ = 44611700-1000^.8,314^.448,2 = 40885365 Дж.

Зміна енергії Гіббса:

ΔG = ΔH – T_ПТ^.ΔS = 44611700 – 448,2^.99535,25 = 0.

Зміна енергії Гельмгольца:

ΔA = ΔG – nRT_ПТ = 0 – 1000^.8,314^.448,2 = -3726335,0 Дж.

Задача 8. Визначить число фаз і число термодинамічних ступенів свободи для фігуративних точок на “полі” діаграми, “лінії” і “точці”.

Розв’язання. Число фаз (Ф) для фігуративних точок на “полі” діаграми дорівнює 1, на “лінії” – 2, в потрійній точці – 3.

За правилом фаз Гіббса

С = К – Ф + n

для однокомпонентної системи (К = 1) і для n = 2 (змінні, що впливають на рівновагу – тиск і температура) число термодинамічних ступенів свободи в “полі” дорівнює

С_П = 1 – 1 + 2 = 2,

на “лінії’

С_Л = 1 – 2 + 2 = 1,

в потрійній точці

С_ПТ = 1 – 3 + 2 = 0.