Лабораторная работа №1

СИНТЕЗ ПРОСТЕЙШИХ АВТОМАТОВ

Цель работы: синтез простейших автоматов, заданных табличным представлением.

1 Теоретическое введение

Триггер является простейшим автоматом. Состояние триггера является его выходом, т.е. триггер является автоматом Мура.

1. Булевы функции

Основная задача теории булевых функций – разработка систематического метода построения сложных функций из более простых.

Число различных булевых функций от m переменных равно , т.е. если m=2, то число различных булевых функций равно Булевы функции для двух переменных p и q приведены в таблице 1.1.

Таблица 1.1

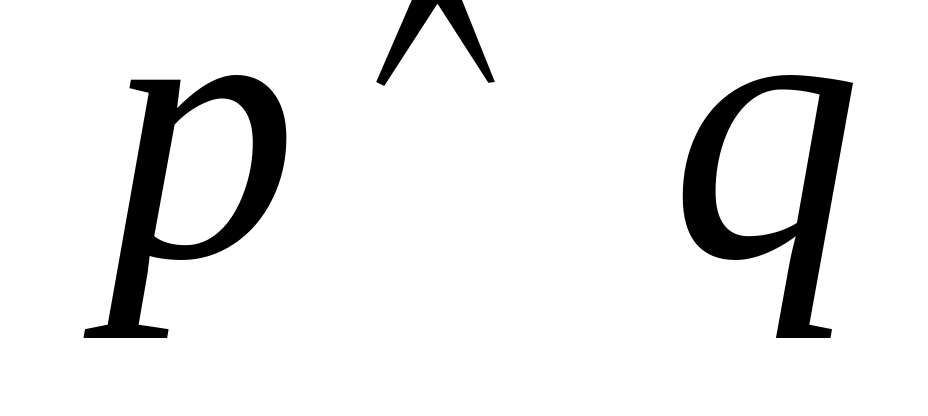
p	q						p│q
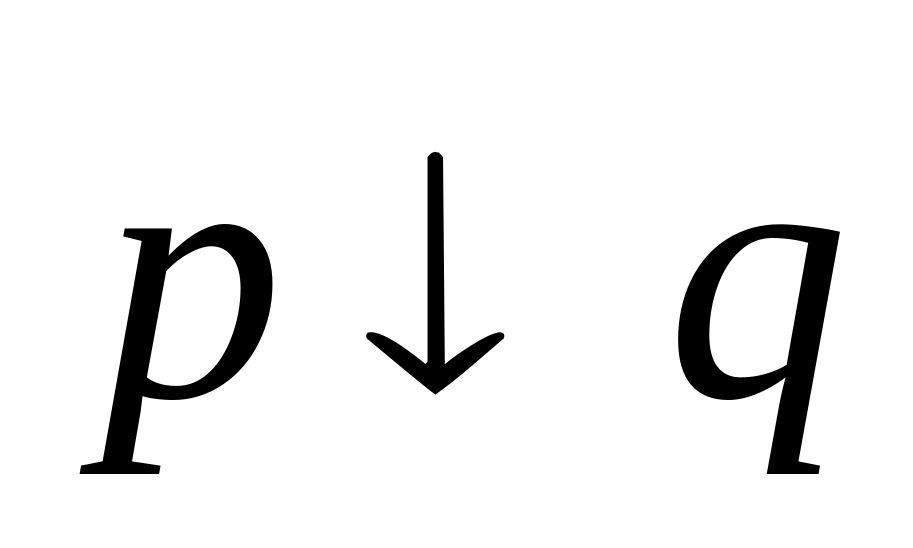
0	0	0	0	1	0	1	1	1
0	1	0	1	1	1	0	1	0
1	0	0	1	0	1	0	1	0
1	1	1	1	1	0	1	0	0

Функция называется функцией И, или конъюнкцией своих аргументов. Знак конъюнкции часто опускают, иногда в качестве знака конъюнкции используют точку или знак &. Функция называется функцией ИЛИ, или дизъюнкцией. Функция называется импликацией или функцией логического следования. Функция - это функция сложения по модулю два (в англоязычной литературе называют XOR). Функция называется функцией эквивалентности (иногда знак эквивалентности обозначают ≡). Функция p│q называется функцией штрих Шеффера (или функция НЕ-И). Функция называется стрелкой Пирса (или функция НЕ-ИЛИ).

Для уменьшения числа скобок при записи логических формул вводят приоритеты операций. Наиболее приоритетна функция отрицания, затем идет конъюнкция, после нее – дизъюнкция. Все другие функции имеют равный приоритет, меньший, чем у дизъюнкции.

Пример

Задана логическая формула (функция трех переменных):

Учитывая приоритетность операций функцию можно эквивалентно записать так:

2. Табличное представление логических формул

Логическая формула дает возможность построить соответствующий функциональный преобразователь. Для рассмотренного примера получаем:

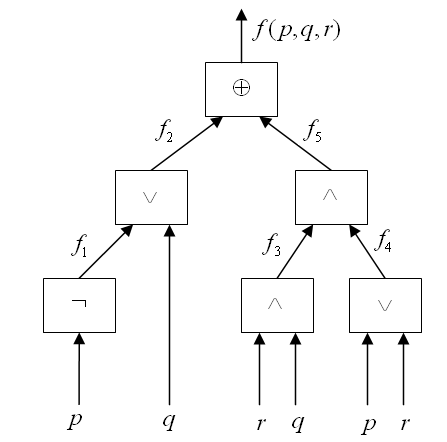
Логическая формула позволяет построить табличное представление функции f(p,q,r).

Таблица 1.2

p	q	r
0	0	0	1	1	0	0	0	1
0	0	1	1	1	0	1	0	1
0	1	0	1	1	0	0	0	1
0	1	1	1	1	1	1	1	0
1	0	0	0	0	0	1	0	0
1	0	1	0	0	0	1	0	0
1	1	0	0	1	0	1	0	1
1	1	1	0	1	1	1	1	0

Очевидно, что суперпозицией нескольких простых булевых функций можно построить более сложную функцию.

Любая двоичная функция может быть представлена как суперпозиция только трех функций: И, ИЛИ, НЕ.

3. Свойства булевых функций

Свойства булевых функций приведены в таблице 1.3:

Таблица 1.3

		Коммутативность
		Ассоциативность
		Дистрибутивность
		Законы де Моргана
		Законы исключенного третьего
		Законы поглощения
		Свойства нуля
		Свойства единицы
		Свойства отрицания
		Свойства импликации
		Свойства сложения по модулю два

4. Дизъюнктивная нормальная форма представления булевой функции

Определение. Представление булевой функции в форме дизъюнкции

где каждый терм K_i (или конъюнкт) представляет собой конъюнкцию взятых с отрицанием или без них двоичных переменных функции, называется дизъюнктивной нормальной формой этой функции (или ДНФ).

Если каждый конъюнкт содержит в точности по одной все (взятые с отрицанием или без них) двоичные переменные функции, ДНФ называется совершенной дизъюнктивной нормальной формой этой функции (или СДНФ).

5. Минимизация булевых функций

Сложность схемы, реализующей булеву функцию, определяется сложностью ее аналитической записи. Т.к. одну и ту же булеву функцию можно представить различными формулами, то стоит задача выбора более простой формулы, т.е. задача выбора минимальной формы булевой функции. Рассмотрим один из способов, позволяющий получить минимальную дизъюнктивную нормальную форму булевой функции (ДНФ) – карта Карно.

Карта Карно – табличная форма представления булевой функции. Каждой клетке в таблице сопоставляется терм СДНФ минимизируемой функции, причем так, что любым осям симметрии таблицы соответствуют зоны, взаимно инверсные по какой-либо переменной, т.е. каждая клетка таблицы отличается знаком инверсии только одной переменной.

Составим карту Карно для функции рассмотренной в примере раздела 1.1. Пользуемся табличным представлением функции (таблица 1.2). Рассматриваемая функция имеет 8 значений, поэтому карта Карно должна иметь 8 клеток:

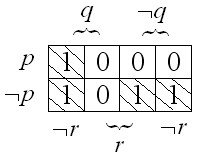
После составления таблицы ее покрывают минимальным числом максимальных квадратов или прямоугольников со сторонами, равными степеням двойки, так, чтобы они обязательно покрыли все единицы и не покрывали ни одного нуля. В результате можем записать минимальную ДНФ для рассматриваемой функции:

6. D – триггеры

D-триггер (от англ. Delay – задержка) имеет асинхронный инверсный вход R (от англ. Reset – сброс) установки триггера в 0, асинхронный инверсный вход S (от англ. Set – установка) установки в 1, синхронный информационный вход D (от англ. Data – данные), синхронизирующий (управляющий) вход C (от англ. Clocking – синхронизация, тактирование), а также прямой выход Q и инверсный выход .

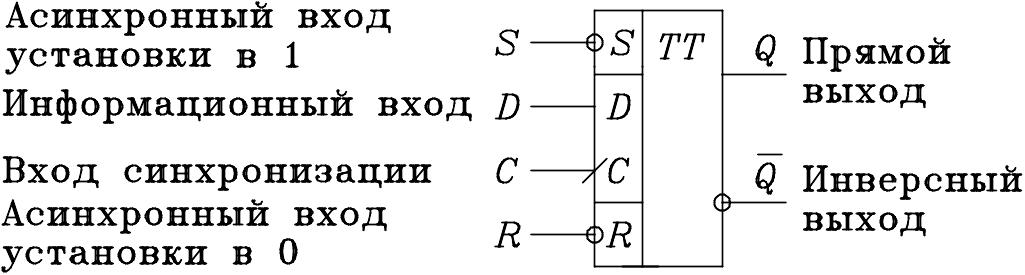
Рис.1.1. D-триггер

Рассматриваемый D-триггер может работать в асинхронном и синхронном режимах.

Работа D-триггера в асинхронном режиме описывается таблице 1.4 и иллюстрируется рисунке 1.2.

Таблица 1.4

Асинхронный режим работы D-триггера

S(t)	R(t)	Q(t)	Q(t+1)	Комментарий
0 0	0 0	0 1	Не определено	Запрещенный набор аргументов S и R
0 0	1 1	0 1	1 1	Установка в 1
1 1	0 0	0 1	0 0	Сброс в 0
1 1	1 1	0 1	0 1	Режим хранения, синхронный режим работы

По входам S и R триггер управляется инверсными сигналами, т.е. активные сигналы имеют уровень логического 0, а пассивные – уровень логической 1. При S = R = 1 триггер находится в режиме хранения. Условие S = R = 1 является обязательным и для синхронного режима работы. Перевести триггер в состояние 0 можно кратковременной подачей на вход R сигнала логического 0. На входе S при этом должен быть сигнал логической 1. Аналогичным образом легко записать в триггер 1: на R-входе надо сохранить логическую 1, а на S-вход кратковременно подать логический 0.

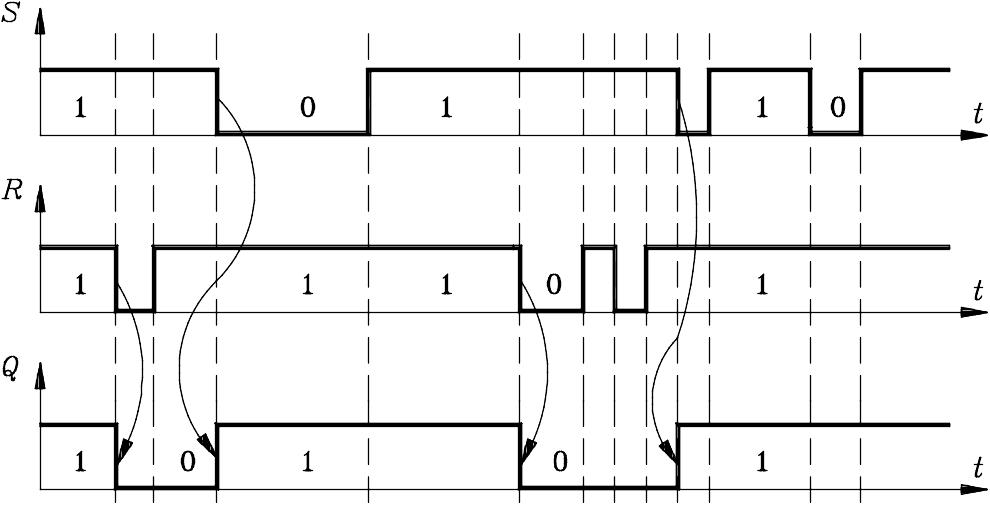
Рис.1.2. Временные диаграммы D-триггера в асинхронном режиме

Одновременная подача нулей на S- и R- входы триггера не рекомендуется, так как триггер перестает нормально работать: на его прямом и инверсном выходах оба сигнала становятся равными 1. Комбинация S = 0, R = 0 считается поэтому запрещенной.

При S = 0 и R = 1 триггер находится в состоянии 1 и на сигналы D и C синхронного управления не реагирует. Аналогичным образом, при S = 1 и R = 0 состояние триггера Q = 0 и не зависит от изменения сигналов на входах D и C.

Синхронный режим работы D-триггера в конечных автоматах является основным.

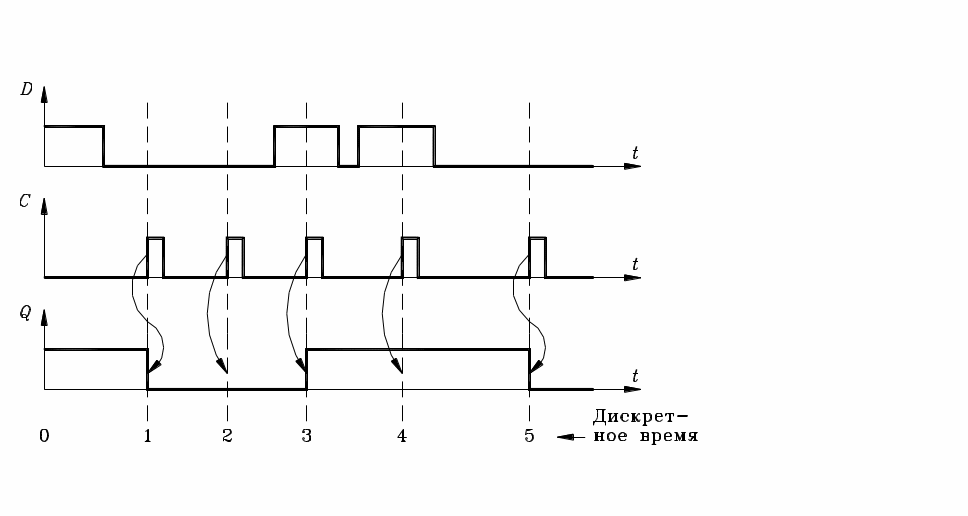
Рис.1.3. Временные диаграммы D-триггера в синхронном режиме

Таблица 1.5

Синхронный режим работы D-триггера

S = R = 1
D(t)	Q(t)	Q(t+1)
0 0 1 1	0 1 0 1	0 0 1 1

1.7 JK - триггер

Триггер имеет асинхронные инверсные входы S и R установки в 1 и сброса в 0 соответственно, вход синхронизации C и синхронные информационные входы J и K с логикой 3И каждый, прямой Q и инверсный выходы.

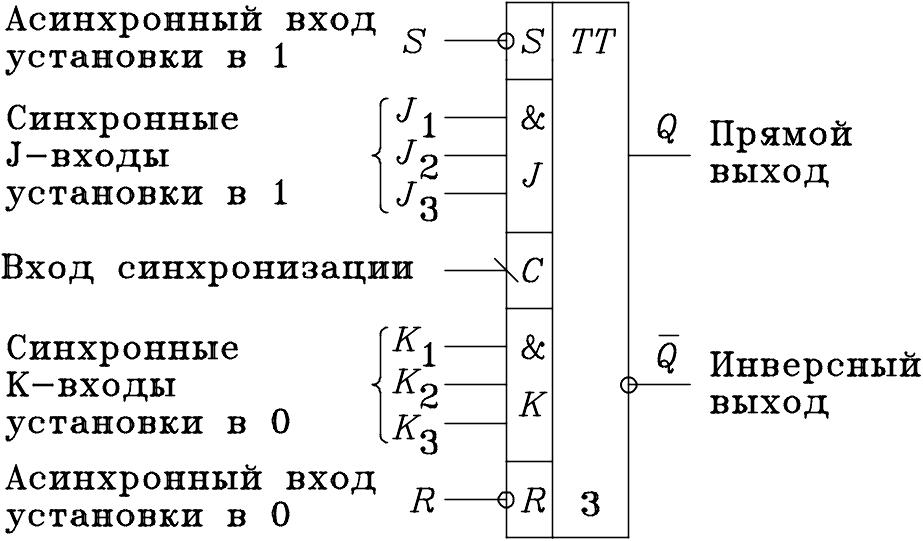
Рис.1.4. JK-триггер

В синхронном режиме работы, основном для конечного автомата, асинхронные входные сигналы должны быть равны 1, т.е. S = R = 1. Временные диаграммы приведены на рис.1.5. Состояние Q JK-триггера изменяется при переходе сигнала синхронизации С из 1 в 0, т.е. по падающему фронту импульса синхронизации.

Анализ таблицы 1.6 показывает, что сочетание сигналов J = 0, K = 0 не изменяет состояние триггера. При J = 0, K = 1 триггер переходит в нулевое состояние, а при J = 1, K = 0 – в единичное, причем независимо от исходного состояния. Сочетание J = 1, K = 1 переводит триггер в счетный режим работы, т.е. состояние JK-триггера изменяется на противоположное каждый раз при поступлении на вход C очередного импульса синхронизации. Таким образом, из одного состояния в другое JK-триггер можно перевести двумя разными способами, т.е. он имеет дублированную систему переходов.

Таблица 1.6

Синхронный режим работы JK-триггера

S=R=1
J(t)	K(t)	Q(t)	Q(t+1)
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 0 0 1 1 1 0

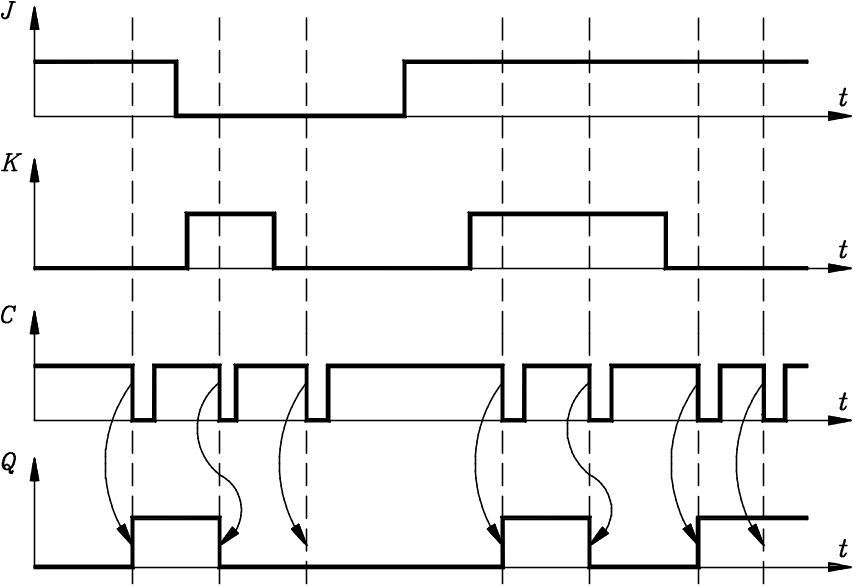
Рисунок 1.5

Временные диаграммы JK-триггера в синхронном режиме (S = R = 1)