
- •Глава II. Дифференциальные уравнения первого порядка, интегрируемые в квадратурах
- •§ 1. Уравнения с разделяющимися переменными
- •Решение типовых примеров
- •Задачи для самостоятельного решения
- •§ 2. Однородные дифференциальные уравнения 1-го порядка.
- •Решение типовых примеров
- •Задачи для самостоятельного решения.
- •§ 3. Дифференциальные уравнения, приводимые к однородным дифференциальным уравнениям первого порядка.
- •Решение типовых примеров
- •Задачи для самостоятельного решения
Глава II. Дифференциальные уравнения первого порядка, интегрируемые в квадратурах
Общий вид дифференциального уравнения 1-го порядка, разрешенного относительно производной, если производную выразить через отношение дифференциалов, следующий:
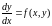 . (1)
. (1)
Рассмотрим основные типы уравнений вида (1), интегрируемых в квадратурах.
§ 1. Уравнения с разделяющимися переменными
Уравнение (1)
называется уравнением
с разделяющимися переменными,
если функция
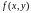 представляет собой произведение функции
переменной
представляет собой произведение функции
переменной
 на функцию переменной
на функцию переменной
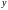 :
:
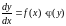 . (2)
. (2)
Предполагая
 и
и
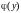 непрерывными в промежутках
непрерывными в промежутках
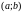 и
и
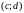 соответственно и
соответственно и
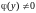 в
,
деля на
и умножая на
в
,
деля на
и умножая на
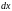 ,
мы добиваемся разделения переменных:
,
мы добиваемся разделения переменных:
 . (3)
. (3)
Функции
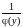 и
непрерывны, а, следовательно, имеют
первообразные:
и
непрерывны, а, следовательно, имеют
первообразные:
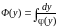 и
и
 .
Поэтому (3) может быть переписано в виде:
.
Поэтому (3) может быть переписано в виде:
 . (4)
. (4)
Из равенства дифференциалов двух функций (здесь рассматривается как функция от , определяемая дифференциальным уравнением) заключаем, что сами функции отличаются на постоянную:
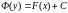 , (5)
, (5)
или
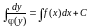 . (6)
. (6)
Соотношение (5), или (6) и представляет собой общий интеграл уравнения (3), так как это соотношение, переписанное в виде
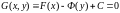 , (7)
, (7)
удовлетворяет
условиям теоремы о неявной функции;
производные
 и
и
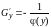 непрерывны в области
непрерывны в области
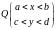 и
и
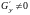 .
Поэтому уравнение (7) определяет
как функцию от
,
непрерывную и дифференцируемую, причем
.
Поэтому уравнение (7) определяет
как функцию от
,
непрерывную и дифференцируемую, причем
 ,
,
т. е. функции, определяемые уравнением (7), а, следовательно, и (6), являются решениями данного дифференциального уравнения.
Замечание
1.
При различных значениях
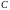 получаются различные функции. При
фиксированном
(выбор
определяется начальными условиями
получаются различные функции. При
фиксированном
(выбор
определяется начальными условиями
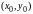 )
решение единственное.
)
решение единственное.
Замечание 2. Всякая функция , являющаяся решением данного уравнения (2), тождественно ему удовлетворяющая, должна удовлетворять и вытекающему из него соотношению (5) или (6). Таким образом, (6) действительно является общим интегралом. Кроме того, из (4) видно, что любые начальные условия из Q однозначным образом определяют надлежащее значение и, следовательно, соответствующее единственное решение.
Таким образом, доказана следующая теорема.
Теорема. Если в уравнении с разделяющимися переменными функции и непрерывны в интервалах и соответственно и , то общий интеграл этого уравнения выражается в квадратурах:
.
причем заданием
начальных условий
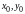 ,
где
‑ любая точка прямоугольника
определяется единственное решение
этого уравнения.
,
где
‑ любая точка прямоугольника
определяется единственное решение
этого уравнения.
Интеграл (7)
дифференциального уравнения, определяющий
решение, удовлетворяющее начальным
условиям, можно переписать в виде:
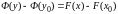 или
или
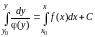
Замечание.
Если
 при некотором
при некотором
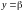 ,
то дифференциальное уравнение (2) имеет
решение
.
Но так как интеграл
,
то дифференциальное уравнение (2) имеет
решение
.
Но так как интеграл
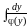 при
не существует (по крайней мере, как
собственный), то это решение не входит
в состав общего интеграла (6). Поэтому,
если
в дифференциальном уравнении
при
не существует (по крайней мере, как
собственный), то это решение не входит
в состав общего интеграла (6). Поэтому,
если
в дифференциальном уравнении
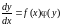 ,
то уравнение, кроме общего интеграла,
имеет еще решение
,
не получающееся из общего. Будет ли при
этом решение
особым? Этот вопрос требует специального
рассмотрения.
,
то уравнение, кроме общего интеграла,
имеет еще решение
,
не получающееся из общего. Будет ли при
этом решение
особым? Этот вопрос требует специального
рассмотрения.
Уравнение с разделяющимися переменными в симметрической форме имеет вид:
 . (8)
. (8)
Разделяя в нем переменные и интегрируя, получаем общий интеграл:
 .
.
При этом, если
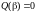 или
или
 ,
то, кроме общего интеграла, будут еще
решения:
и
,
то, кроме общего интеграла, будут еще
решения:
и
 ,
не получаемые из общего; соответствующие
им интегральные кривые – прямые,
параллельные осям координат.
,
не получаемые из общего; соответствующие
им интегральные кривые – прямые,
параллельные осям координат.
Интеграл, удовлетворяющий начальным условиям , запишется в виде:
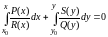 .
.
