1.1. Представление сложных динамических процессов в виде дискретных систем

В качестве типичного примера клеточного автомата обычно приводят компьютерную игру “Жизнь”, которую еще в 1970 г. создал для учебных целей английский математик  Дж.Конвей.

Эта игра упрощенно моделирует эволюцию, развитие и взаимодействие колоний микроорганизмов.  В ней рассматривается бесконечная плоская решетка квадратных элементов-клеток.  Правила этой игры следующие: каждый элемент может находиться в состоянии покоя или активности; элемент переходит из состояния покоя в активное состояние, если по соседству с ним оказались три активных элемента, причем в число соседей включены только четыре ближайших элемента на квадратной решетке. Время в этой игре дискретно (t = 1,2,... k). Каждый элемент решетки может быть “живым” (в нем есть микроорганизмы) или “мертвым” (микроорганизмов нет). Живые элементы можно отметить черным цветом, а мертвые - белым. Состояние каждого элемента может меняться в моменты времени t = 1,2,3... У каждого элемента есть восемь соседей, которые имеют с ним общие ребра и вершины.

Пусть в бесконечной цепочке клеток каждая клетка может находиться в состоянии “покоя” или “возбуждения”. Можно говорить в этом контексте и о “живой” или “мертвой” клетке. “Возбужденная в момент t  времени клетка посылает сигнал, который в момент времени доходит до соседних клеток. Клетка возбуждается (“живет”) в том и только в том случае, если к ней приходит сигнал от одной из соседних клеток. Если же сигналы приходят с двух сторон, то клетка не возбуждается. (Если проводить аналогию с живыми организмами, это может означать, что “теснота”, недостаток ресурса делают невозможным размножение, и численность популяции сокращается).  Для такого автомата, зная, сколько клеток возбуждено в начальный момент времени,  можно уже предсказать, сколько клеток будет возбуждено через t  секунд. Наглядный эффект получается при моделировании такого клеточного автомата на экране дисплея. Нетрудно видеть, что картину, возникающую на экране, можно рассматривать как фрактальную структуру. (см. рисунок 3.2). Картина становится сложнее, если мы введем уже не одну начальную клетку, а несколько, однако и здесь можно наблюдать масштабную инвариантность, а это означает, что структура системы фрактальна. Она получила название «Ковер Серпинского».

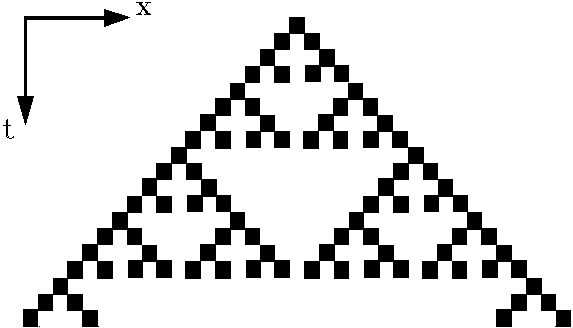
1.2. Моделирование процесса роста с помощью клеточного автомата

Выше было отмечено, что модель такого клеточного автомата также можно использовать для иллюстрации процесса роста популяции. Образующиеся “пустоты” внутри фрактальной структуры, отображающей динамику развития популяции, можно интерпретировать как уменьшение популяции вследствие “выедания” пищевого ресурса. Однако в реальных условиях невозможно такое математически “правильное” развитие процесса. Можно моделировать, например, определенный процент смертности внутри популяции из-за различных причин (хищники, болезни, неблагоприятные абиотические факторы, случайная гибель). Такая смертность носит стохастический характер и моделируется с помощью так называемого генератора случайных чисел и задаваемой величины риска гибели для отдельных “клеток-индивидуумов”. При таком моделировании получаются самые различные варианты развития процесса, и, начиная с некоторого значения риска, для каждого варианта начальных условий возникают условия, когда популяция не может далее развиваться или поддерживать свою жизнедеятельность и гибнет.

Наверх