Подставляем в (1) и интегрируем результат

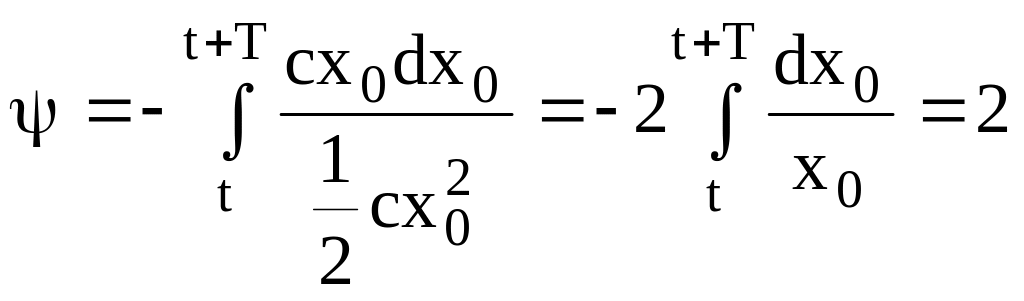ln (2)

Здесь введено обозначение для логарифмического декремента колебаний

ln

В формулы динамического расчёта коэффициент поглощения часто входит в виде отношения к числу а именно через коэффициент неупругого сопротивления

(3)

Конкретные значения коэффициентов определяются конструкцией, материалом и другими собственными свойствами колебательной системы. Для строительных материалов значения следующие:

бетон и железобетон - 0,1; кирпичная кладка - 0,08;

дерево - 0,05; прокатная сталь - 0,025.

Е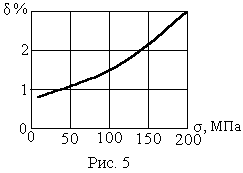 сть многочисленные таблицы и графики (типа, изображённого на рис. 5) зависимости (напряжение - логарифмический декремент) для разных материалов, с учётом технологических обработок материала, температуры, для различных видов деформаций: растяжение, изгиб, кручение и т. д.

Есть литературные данные [5] о значениях коэффициентов поглощения в стыках конструкций, резьбовых соединениях, шпоночных и шлицевых соединениях, подшипниках, в тросах и канатах и т. д.

Г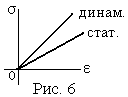 ипотеза Фойгта (1850 – 1919 г.г.). Обобщая закон Гука на динамическое нагружение материала, Фойгт предложил гипотезу о вязкоупругом деформировании (рис. 6), выражаемую формулой

(4)

где - коэффициент вязкости материала, - скорость изменения деформации. Она оказалась сравнительно удобной для использования в уравнениях колебаний. Но гипотеза Фойгта имеет очевидную неточность («дефект»), заключающуюся в следующем. Можно показать, что использование (4), даёт формулу для коэффициента поглощения энергии

. (5)

Здесь - частота колебаний. В силу (5), (2),

. (6)

Ф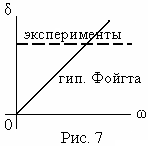 ормула (6) показывает, что логарифмический декремент является частотно – зависимой величиной (рис. 7, сплошная линия). Между тем многочисленные опыты показывают, что значение остается постоянной величиной в широком диапазоне значений (рис. 7, пунктирная линия). Поэтому гипотеза Фойгта, вообще-то говоря, даёт неверные результаты. Но ею можно пользоваться вблизи точки пересечения сплошной и пунктирной линий, или при колебаниях, далеких от резонанса, так как для таких колебаний небольшие значения внутреннего трения не играют почти никакой роли.

Этот «дефект» можно исправить. Для этого перепишем (3) в виде

. (7)

Коэффициент вязкости материала найдем таким, чтобы (5) и (7) давали одинаковые результаты, т. е. имели равные правые части

.

Отсюда

и (6) принимает вид

. (8)

В результате логарифмический декремент колебаний стал частотно - независимым.