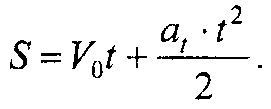4. Ускорение точки и виды движения точки в зависимости от ускорения

Ускорение есть кинематическая мера изменения скорости точки.

Прямолинейное движение. При прямолинейном движении точки вектор скорости всегда совпадает с траекторией, поэтому вектор изменения ускорения также совпадает с траекторией.

Если за небольшой промежуток времени Δ t скорость точки изменилась на ΔV, то среднее ускорение будет:

Истинное ускорение есть предел, к которому стремится среднее ускорение при А/, стремящемся к нулю, т.е.

Таким образом, учитывая, что

получим

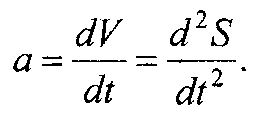
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты по времени.

Единица ускорения:

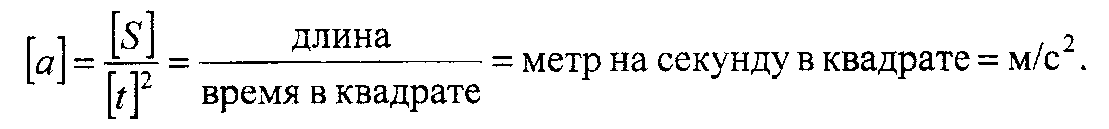
Пример 1.

Точка движется прямолинейно по закону S = t⁴ +2t (S - в метрах, t - в секундах). Найти ее среднее ускорение в промежутке между моментами t₁ = 5 с, t₂ = 7 с, а также ее истинное ускорение в момент t₃ = 6 с.

Решение.

1. Находим скорость движения точки как производную от пути S по времени t, т.е.

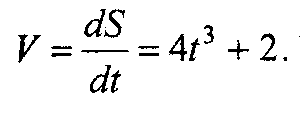
2. Подставляя вместо t его значения t₁ = 5 с и t₂ = 7 с, находим скорости:

V₁ = 4 • 5³ + 2 = 502 м/с; V₂ = 4 • 7³ + 2=1374 м/с.

3. Определяем приращение скорости ΔV за время Δt = 7 - 5 =2 с:

ΔV = V₂ - V₁ = 1374 - 502 = 872 м/с.

4. Таким образом, среднее ускорение точки будет равно

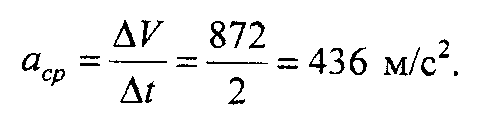
5. Для определения истинного значения ускорения точки берем производную скорости по времени:

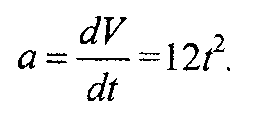
6. Подставляя вместо t значение t₃ = 6 с, получим ускорение в этот момент времени

a_ср=12-6³=432 м/с².

Криволинейное движение. При криволинейном движении скорость точки изменяется по величине и направлению.

Представим себе точку М, которая за время Δt, двигаясь по какой-то криволинейной траектории, переместилась в положение М₁ (рис. 6).

Вектор приращения (изменения) скорости ΔV будет

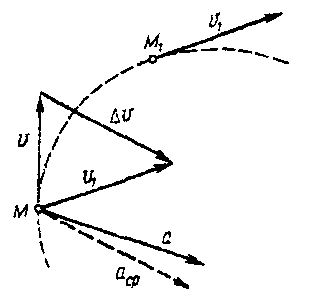
Рис. 6

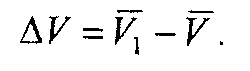
Для нахождения вектора ΔV перенесем вектор V₁, в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:

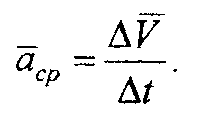
Вектор а_ср параллелен вектору ΔV , так как от деления вектора на скалярную величину направление вектора не изменяется. Вектор истинного ускорения есть предел, к которому стремится отношение вектора скорости к соответствующему промежутку времени Δt, стремящемуся к нулю, т.е.

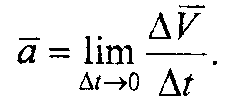
Такой предел называют векторной производной.

Таким образом, истинное ускорение точки при криволинейном движении равно векторной производной по скорости.

Из рис. 6 видно, что вектор ускорения при криволинейном движении всегда направлен в сторону вогнутости траектории.

Для удобства расчетов ускорение раскладывают на две составляющие к траектории движения: по касательной, называемое касательным (тангенциальным) ускорением а,, и по нормали, называемое нор-мальным ускорением а_n (рис. 7).

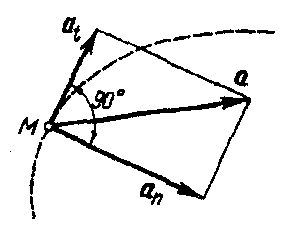
Рис. 7

В этом случае полное ускорение будет равно

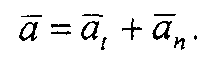
Касательное ускорение совпадает по направлению со скоростью точки или противоположно ей. Оно характеризует изменение величины скорости и соответственно определяется по формуле

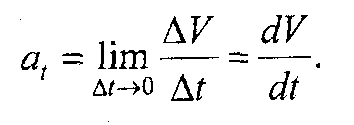
Нормальное ускорение перпендикулярно к направлению скорости точки, а численное значение его определяется по формуле

где r - радиус кривизны траектории в рассматриваемой точке.

Так как касательное и нормальные ускорения взаимно перпендикулярны, поэтому величина полного ускорения определяется по формуле

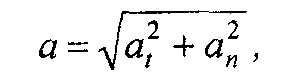
а направление его

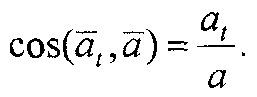
Если 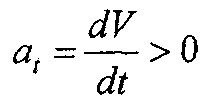, то векторы касательного ускорения и скорости направлены в одну сторону и движение будет ускоренным.

Если , то вектор касательного ускорения направлен в сторону, противоположную вектору скорости, и движение будет замедленным.

Вектор нормального ускорения всегда направлен к центру кривизны, поэтому оно называется центростремительным.

Пример 2.

Точка обода маховика двигателя в период разгона движется согласно закону S = 0,2t³ (S - в метрах, t - в секундах). Радиус маховика r = 0,8 м. Определить касательное и нормальное ускорения точки в момент, когда ее скорость V = 20 м/с.

Решение.

1. Определяем время разгона маховика при скорости V = 20 м/с, для чего вычислим производную пути по времени, т.е.

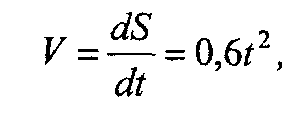
откуда время t будет

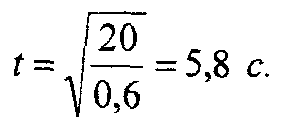
2. Для этого момента времени находим касательное ускорение как производную скорости по времени:

3. Находим нормальное ускорение в конце разгона маховика, т.е.

Анализируя приведенные формулы касательного и нормального ускорений, можно установить следующие виды движения точки (рис. 8).

Рис. 8.

1. Равномерное прямолинейное движение (рис. 8, а). В

этом случае касательное ускорение равно нулю, так как величина скорости не изменяется (ΔV = 0) и нормальное ускорение равно нулю, так как r = ∞, т.е.

Значит и полное ускорение равно нулю: a = 0.

2. Равномерное криволинейное движение (рис. 8, б). Оно характеризуется тем, что численное значение скорости постоянно (V = const), а вектор скорости меняется (r ≠ ∞), т.е.

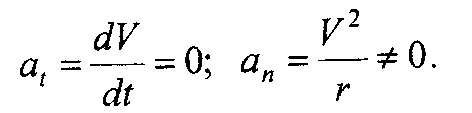
Полное ускорение при этом движении равно нормальному ускорению:

а =а_n

3. Неравномерное прямолинейное движение (рис. 27, в) характеризуется тем, что модуль скорости движения точки изменяется (ΔV ≠ 0), а радиус кривизны траектории движения точки равен бесконечности (r = со). В этом случае касательное ускорение не равно нулю, а нормальное равно нулю, т.е.

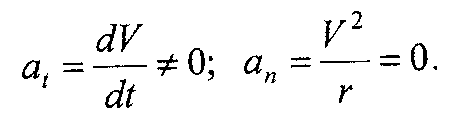
Полное ускорение в этом случае будет

а = а_t

4. Неравномерное криволинейное движение (рис. 27, г) характерно тем, что скорость движения непостоянна (V ≠ const) и вектор скорости изменяется (r ≠ ∞). В этом случае касательное и нормальное ускорения не равны нулю, т.е.

Полное ускорение складывается геометрически из касательного и нормального ускорений:

5. Равнопеременное движение точки характеризуется тем, что если нормальное ускорение не равно нулю (а_n ≠ 0), то имеет место криволинейное движение, а если а_n = 0 - прямолинейное. В этом случае касательное ускорение есть величина постоянная, т.е.

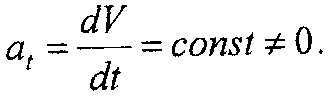
Формулы равнопеременного движения точки. Равнопеременное движение может быть равномерно ускоренным, если численное значение скорости увеличивается, и равномерно замедленным, если численное значение скорости уменьшается. Величину ускорения можно определить через значения скорости в начале и в конце произвольного промежутка времени t, т.е.

где V₀ - начальная скорость.

Преобразуя формулу касательного ускорения находим значение скорости:

V = V₀ + a_t, t.

При равномерно ускоренном движении ускорение а_t имеет положительное значение, а при равномерно замедленном - отрицательное.

Пусть, пройденный точкой при равнопеременном движении, определяется из уравнения:

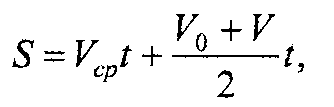
откуда после подстановки значения скорости и преобразований получим уравнение пройденного точкой пути, т.е.

13