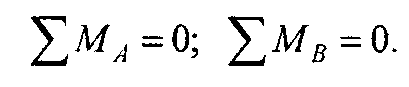3. Опоры и опорные реакции балочных систем

В машинах и конструкциях очень часто встречаются тела удлиненной формы, называемые балками или балочными системами. Балки предназначены, в основном, для восприятия поперечных нагрузок, а балочные системы имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий.

Опоры балок могут быть разделены на три основных типа: шарнирно-подвижные, шарнирно-неподвижные, жесткая заделка. Рассмотрим правило для определения направления реакций связей на них.

Шарнирно-подвижная опора (рис. 5, опора А) допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Реакция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю.

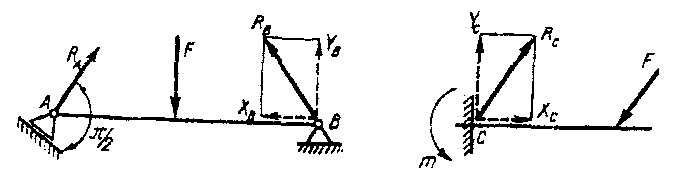
Рис. 5

Шарнирно-неподвижная опора (рис. 5, опора В) допускает только поворот вокруг оси и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и ее направление заранее неизвестны (два неизвестных). В этих случаях при решении задач такую реакцию разлагают на две взаимно перпендикулярные составляющие Xв и Ув , неизвестные по модулю, но известные по направлению.

Жесткая заделка (защемление) показана на рис. 5, опора С. Она не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой R_c , неизвестной по модулю и направлению и поэтому разлагаемую на две составляющие Х_с и У_с и реактивным моментом т (три неизвестных).

Кроме перечисленных основных типов опор балок, в конструкциях нередко балка свободно опирается на плоскость (поверхность) или на ребро призмы. В этих случаях реакции определяют по правилам, изложенным вп. 1.1.2.

4. Распределённые нагрузки

До сих пор мы имели дело с силами, приложенными в точке, которые называют сосредоточенными. Но в практике часто встречаются силы, приложенные равномерно или считаются приложенными равномерно по объему поверхности тела, например, сила тяжести, давление ветра, снега, воды и т.п. Такие силы называются распределенными.

Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой q. Интенсивность есть сила, приходящаяся на единицу длины нагруженного участка. Интенсивность в системе СИ выражается в Н/м.

Распределенная нагрузка, имеющая постоянную интенсивность, называется равномерно распределенной (рис. 6).

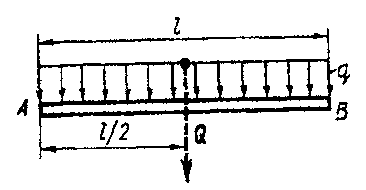
Рис. 6.

При решении задач статики распределенную нагрузку заменяют равнодействующей (сосредоточенной), модуль которой определяется по формуле

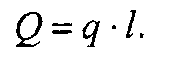
Приложена равнодействующая Q в середине отрезка АВ.

Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной. Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину.

5. Уравнения равновесия плоской системы сил.

Плоская система сил может быть приведена к главному вектору R' и главному моменту М₀, поэтому условия равновесия сил на плоскости имеют вид

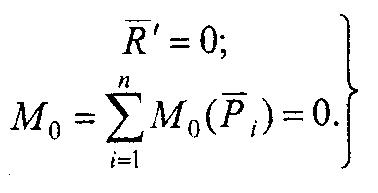
Итак, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат равнялись нулю и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Величину главного вектора можно определить через проекции всех сил системы на координатные оси х и у. Для равновесия необходимо, чтобы главный вектор был равен нулю. При соблюдении этого условия получим:

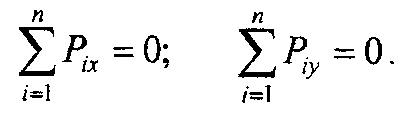
Кроме того, для равновесия необходимо, чтобы главный момент также был равен нулю, т.е.

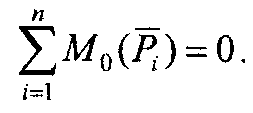
В дальнейшем для уравнения равновесия при решении задач будем применять более компактную схему записи, не применяя при букве Σ обозначения i = 1 и п.

Уравнения равновесия произвольной плоской системы сил могут быть представлены в трех формах.

1. Основная форма приведена выше:

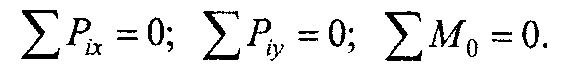
2. Выбрав три произвольные точки А, В, С и приравняв нулю сумму моментов относительно каждой из них, можно получить следующие три уравнения равновесия:

3. Эта форма представляет собой равенство нулю сумм моментов относительно двух произвольных точек А и В и равенство нулю суммы проекций на некоторую ось х, т.е.

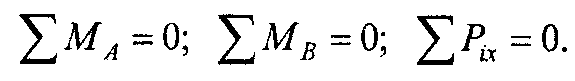
При пользовании этой формулой необходимо, чтобы ось х не была перпендикулярна линии, соединяющей точки А и В.

Для системы параллельных сил, выбрав одну из осей проекций параллельной этим силам, а другую - перпендикулярной к ним, получим существенные упрощения.

Первая форма уравнений равновесия в этом случае примет вид

Вторая и третья формы уравнений равновесия примут одинаковый вид