
- •Предисловие
- •Введение
- •Глава 1. Случайные события
- •§1. Элементы комбинаторики
- •§2. Основные понятия теории вероятностей
- •2.1. Опыт и событие. Классификация событий
- •2.2. Операции сложения и умножения над событиями.
- •§3. Вероятность. Классическое определение вероятности Геометрическая вероятность. Статистическая вероятность
- •3.1. Классическое определение вероятности
- •3.2. Геометрическая вероятность
- •3.3. Статистическая вероятность
- •Глава 2. Теоремы сложения и умножения вероятностей
- •§1. Теорема сложения вероятностей
- •§2. Теорема умножения вероятностей.
- •§3. Формула полной вероятности. Формулы Байеса
- •Глава 3. Повторные независимые испытания
- •§1. Схема Бернулли. Формула Бернулли
- •Формула Бернулли
- •§2. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
- •§3. Наивероятнейшее число появлений события
- •Глава 4. Случайные величины
- •§1. Понятие случайной величины
- •§2. Закон распределения дискретной случайной величины Многоугольник распределения
- •§3. Функция распределения вероятностей случайной величины
- •§4. Плотность распределения вероятностей случайной величины
- •§5. Числовые характеристики случайных величин
- •Математическое ожидание случайной величины
- •2. Дисперсия случайной величин.
- •3. Среднее квадратическое отклонение
- •Мода случайной величины
- •Глава 5. Некоторые законы распределения случайных величин
- •§1. Биномиальное распределение
- •§2. Распределение Пуассона
- •§3. Нормальное распределение непрерывной случайной величины
- •Основные задачи, связанные с нормальным распределением
- •Правило «трех сигм»
- •Индивидуальные задания для внеаудиторной работы.
- •Заключение
- •Библиографический список:
§2. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
Если
вероятность p
наступления события
в каждом
испытании постоянна и близка к 0 (р<0,1),
а число n независимых
испытаний достаточно велико, причем
выполняется условие
![]() ,
где
,
где![]() ,
то вероятность
того, что событие произойдет m
раз в п
испытаниях,
равна
,
то вероятность
того, что событие произойдет m
раз в п
испытаниях,
равна
![]() . (2)
. (2)
Формулу (2) называют формулой Пуассона.
Формула Пуассона находит применение в теории массового обслуживания и в теории надежности.
Теорема
(локальная теорема Муавра-Лапласа). Если
вероятность
p
наступления
события A
в каждом испытании постоянна,
![]()
(p не близка к 0), а число n независимых испытаний достаточно велико, то вероятность может быть вычислена по приближенной формуле (тем точнее, чем больше n):
![]() ,
где
,
где
![]() (3)
(3)
Формулу (3) называют формулой Муавра-Лапласа.
Введем
функцию
![]() ,
тогда формула (3) принимает вид
,
тогда формула (3) принимает вид
![]() ,
,
Функцию
![]() называют функцией Гаусса, ее график –
кривой вероятностей (рис. 5).
называют функцией Гаусса, ее график –
кривой вероятностей (рис. 5).
Д ля
функции
составлены таблицы значений (см.
приложение 1)
ля
функции
составлены таблицы значений (см.
приложение 1)
Пользуясь таблицами значений, следует учитывать следующие свойства функции :
1.
Функция
– четная, т.е.
![]() .
.
2.
Если
![]() ,
то
,
то
![]() .
.
Рис. 5.
Формулы
Бернулли, Пуассона, Муавра-Лапласа
применяют тогда, когда нужно определить
вероятность появления интересующего
нас события A
ровно m
раз. В тех случаях, когда требуется
вычислить вероятность того, что в n
испытаниях событие A
появится не менее
![]() раз, но не более
раз, но не более
![]() раз (т.е.
раз (т.е.
![]() ),
используют интегральную теорему
Муавра-Лапласа.
),
используют интегральную теорему
Муавра-Лапласа.
Теорема (интегральная теорема Муавра-Лапласа).Если вероятность p события A в каждом испытании постоянна (0<p<1), то вероятность может быть вычислена по приближенной формуле (тем точнее, чем больше п):
 ,
где
,
где
![]() ,
,
![]()
или
![]() ,
где
,
где
![]() –
функция Лапласа.
–
функция Лапласа.
![]() (интеграл
в элементарных функциях не берется,
составлены таблицы значения функции
(см.
приложение 2). График функции
изображен на рис. 6.
(интеграл
в элементарных функциях не берется,
составлены таблицы значения функции
(см.
приложение 2). График функции
изображен на рис. 6.

Пользуясь таблицами значений, следует учитывать следующие свойства функции :
1.
Функция
нечетная,
т.е.
![]() .
.
2.
Если
(![]() ),
то
),
то
![]()
![]()
Рис. 6.
Задача 2. На лекции по теории вероятностей присутствуют 50 студентов. Какова вероятность того, среди них есть 5 студентов, у которых день рождения в январе?
Решение.
Вероятность того, что у наугад взятого
студента день рождения в январе, равна
![]() .
Т.к. вероятность p<0,1,
.
Т.к. вероятность p<0,1,
![]() (т.е. 0<a<10),
то для вычисления вероятности интересующего
нас события воспользуемся формулой
Пуассона.
(т.е. 0<a<10),
то для вычисления вероятности интересующего
нас события воспользуемся формулой
Пуассона.
![]()
Задача 3. Партия яиц считается годной, если 80% яиц удовлетворяют нормам приемки. Какова вероятность при случайном отборе 100 яиц обнаружить:
1) 18 не удовлетворяющих нормам приемки (нестандартных) яиц;
2) от 10 до 20 нестандартных яиц.
Решение.
1)
Т.к. интересующее
нас событие состоит в том, что 18 яиц
являются нестандартными, то обозначим
p
- вероятность того, что случайно взятое
яйцо нестандартное и
![]() ,
,
![]() .
.
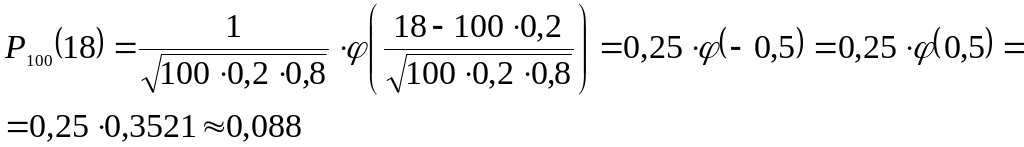
2)
Т.к. необходимо найти вероятность
появления события от
![]() до
до
![]() раз, то воспользуемся интегральной
теоремой Муавра-Лапласа:
раз, то воспользуемся интегральной
теоремой Муавра-Лапласа:

