
- •Предисловие
- •Введение
- •Глава 1. Случайные события
- •§1. Элементы комбинаторики
- •§2. Основные понятия теории вероятностей
- •2.1. Опыт и событие. Классификация событий
- •2.2. Операции сложения и умножения над событиями.
- •§3. Вероятность. Классическое определение вероятности Геометрическая вероятность. Статистическая вероятность
- •3.1. Классическое определение вероятности
- •3.2. Геометрическая вероятность
- •3.3. Статистическая вероятность
- •Глава 2. Теоремы сложения и умножения вероятностей
- •§1. Теорема сложения вероятностей
- •§2. Теорема умножения вероятностей.
- •§3. Формула полной вероятности. Формулы Байеса
- •Глава 3. Повторные независимые испытания
- •§1. Схема Бернулли. Формула Бернулли
- •Формула Бернулли
- •§2. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
- •§3. Наивероятнейшее число появлений события
- •Глава 4. Случайные величины
- •§1. Понятие случайной величины
- •§2. Закон распределения дискретной случайной величины Многоугольник распределения
- •§3. Функция распределения вероятностей случайной величины
- •§4. Плотность распределения вероятностей случайной величины
- •§5. Числовые характеристики случайных величин
- •Математическое ожидание случайной величины
- •2. Дисперсия случайной величин.
- •3. Среднее квадратическое отклонение
- •Мода случайной величины
- •Глава 5. Некоторые законы распределения случайных величин
- •§1. Биномиальное распределение
- •§2. Распределение Пуассона
- •§3. Нормальное распределение непрерывной случайной величины
- •Основные задачи, связанные с нормальным распределением
- •Правило «трех сигм»
- •Индивидуальные задания для внеаудиторной работы.
- •Заключение
- •Библиографический список:
2.2. Операции сложения и умножения над событиями.
1. Суммой двух событий называется событие, состоящее в появлении хотя бы одного из них.
Обозначение: А+В.
Замечание. Операция сложения определена и для большего числа событий.
Пример. Турист имеет возможность посетить 3 города. Обозначим события:
А – турист посетит город А;
В – турист посетит город В;
С – турист посетит город С.
Событие А+В состоит в том, что турист посетит только один из городов А или В, или он посетит их оба.
Событие А+В+С состоит в том, что турист посетит только один из городов А,В,С или пары городов А,В или А,С или В,С или он посетит все три города.
Геометрическая иллюстрация суммы двух событий:
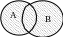
Рис.1.
А+В – изображена всей заштрихованной областью.
2. Произведением двух событий называют событие, состоящее в одновременном их появлении.
Обозначение:
![]() или АВ.
или АВ.
Пример. Рассмотрим события:
А – из колоды карт вытянули «даму»;
В – из колоды карт вытянули карту пиковой масти.
Событие АВ – из колоды карт вытянули «даму» пиковой масти.
Геометрическая иллюстрация произведения двух событий:

Рис.2.
АВ – выделенная область (обведена жирной линией).
Замечание. Аналогично определяется и обозначается произведение в случае большего числа событий.
Пример. Рассмотрим события:
А – попадание по мишени при первом выстреле;
В – попадание по мишени при втором выстреле;
С – попадание по мишени при третьем выстреле.
Событие АВС – три попадания по мишени при трех выстрелах.
Используя операции сложения и умножения, можно сложное событие разложить на более простые и наоборот.
Пример. Рассмотрим события:
А – попадание по мишени при первом выстреле;
В – попадание по мишени при втором выстреле;
С – попадание по мишени при третьем выстреле.
События, противоположные А, В, С:
–
промах
при первом выстреле;
![]() –
промах при втором выстреле;
–
промах при втором выстреле;
![]() – промах при третьем выстреле.
– промах при третьем выстреле.
Событие D – ровно одно попадание при трех выстрелах можно записать с помощью операций сложения и умножения над событиями А, В, С:
D=![]() ,
где
,
где
![]() –
попадание только при первом выстреле,
–
попадание только при первом выстреле,
![]() – попадание
только при втором выстреле,
– попадание
только при втором выстреле,
![]() - попадание только при третьем выстреле.
- попадание только при третьем выстреле.
Событие E – ровно два попадания при трех выстрелах :
E
=![]() ,
где
,
где
![]() – попадание при первом и втором
выстрелах,
– попадание при первом и втором
выстрелах,
![]() – попадание при первом и третьем
выстрелах,
– попадание при первом и третьем
выстрелах,
![]() – попадание при втором и третьем
выстрелах.
– попадание при втором и третьем
выстрелах.
Событие F – хотя бы одно попадание при трех выстрелах :
![]() +
+![]()
![]() ,
где ABC
–попадание
при каждом выстреле.
,
где ABC
–попадание
при каждом выстреле.
§3. Вероятность. Классическое определение вероятности Геометрическая вероятность. Статистическая вероятность
Вероятность – числовая характеристика возможностей появления случайного события в определенных условиях, которые могут быть воспроизведены неограниченное число раз.
Вероятность обозначают буквой P (по первой букве латинского слова probabilitas – вероятность).
В XVIII веке сложилось понятие классической вероятности.
3.1. Классическое определение вероятности
Определение. Вероятностью события называется отношение числа m элементарных исходов, благоприятствующих данному событию, к числу n всех равновозможных, образующих полную группу элементарных исходов опыта.
Обозначение:
![]() – вероятность
события
– вероятность
события
![]() ,
,
![]() .
.
Задача 1. В лотерее 1000 билетов, среди которых 20 выигрышных. Приобретен один билет. Какова вероятность того, что этот билет:
а) выигрышный;
б) невыигрышный.
Решение. а) Событие A – “приобретен выигрышный билет”. Общее число исходов n=1000, число исходов, благоприятных для события A: m=20, тогда
![]() .
.
б) Событие B – “приобретен невыигрышный билет”. Общее число исходов n=1000, число исходов, благоприятных для события B: m=1000-20=980 (число невыигрышных билетов), тогда
![]() .
.
Задача 2. Брошены 2 монеты. Какова вероятность того, что появятся:
а) два орла;
б) орел и решка?
Решение. Составим таблицу вариантов, позволяющих определить все возможные исходы в результате подбрасывания двух монет. В таблице появление орла обозначено буквой О, а появление решки – буквой Р.
1 монета 2 монета |
О |
Р |
О |
ОО |
РО |
Р |
ОР |
РР |
Из таблицы видно, что общее число исходов n при подбрасывании двух монет равно 4 (ОО, РО, ОР, РР), т.е. n=4.
Событие A – появление 2-х орлов. Событию A благоприятствует только 1 исход (ОО), т.е. m=1, тогда
 ;
;
Событие B – появление орла и решки. Событию B благоприятствуют 2 исхода (РО, ОР), т.е. m=2, тогда
 .
.
Задача 3. В группе 20 студентов, из них 9 юношей. Два человека из группы получают индивидуальное задание по некоторому предмету. Какова вероятность того, что это задание выдали двум девушкам?
Решение. Пусть A – событие, вероятность которого нужно найти, .
n
– число всех исходов испытания состоит
в отборе 2-х студентов из 20. В этой выборке
важен только состав, порядок роли не
играет; следовательно, по формуле
подсчета числа сочетаний
![]() имеем
имеем
![]()
m – число благоприятствующих исходов. Для нахождения m следует определить число способов выбора 2 девушек из 11 имеющихся (20-9=11). Для выборки важен только состав. По формуле подсчета числа сочетаний имеем:
![]()
По
определению вероятности:
![]()
Классическая вероятность имеет ограниченную область применения. Применяя классическое определение вероятности, предполагается выполнение условий:
число всех элементарных исходов конечно;
2) все элементарные исходы равновозможны.
На практике часто встречаются опыты, для которых множество исходов бесконечно или эти исходы не являются равновозможными. Возникает необходимость введения других определений вероятности (геометрическая вероятность, статистическая вероятность).
