1. Математическое ожидание случайной величины

Определение. Математическим ожиданием дискретной случайной величины X называют сумму произведений всех возможных значений этой величины на соответствующие вероятности их появления.

Обозначение: М(Х) – математическое ожидание случайной величины X.

M(X)= , где – значение случайной величины, – вероятность появления значения случайной величины.

Определение. Математическим ожиданием непрерывной случайной величины X, все возможные значения которой принадлежат [a;b], называют число, определяемое по формуле – плотность вероятности непрерывной случайной величины Х.

Замечание. Если непрерывная случайная величина X распределена на всей числовой оси, то , при условии того, что несобственный интеграл сходится абсолютно, т.е. где а – некоторое число

Вероятностный смысл математического ожидания состоит в том, что математическое ожидание является средним значением СВ.

Свойства математического ожидания.

М(С)=С, где C-const.

1. Математическое ожидание постоянной величины равно значению этой величины.

2. М(CX)=СM(X), где C-const.

Постоянный множитель можно выносить за знак математического ожидания.

2. М(X+Y)=M(X)+M(Y).

Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

Следствие. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий, т.е. М(X-Y)=M(X)-M(Y).

4. .

Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

5. M(X)

Математическое ожидание случайной величины заключено между наибольшим и наименьшим ее значениями.

6. М(X-M(X))=0, где X –М(X) – отклонение СВ Х от математического ожидания.

Математическое ожидание отклонения СВ Х от математического ожидания равно 0.

Доказательство свойств можно провести, используя определение математического ожидания.

Задача 6. Дискретная случайная величина Х задана законом распределения:

Х	2	1	0
Р	0,48	0,44	y

Найти: y, М(Х).

Решение. y=1-(0,48+0,44)=0,08.

По определению математического ожидания ДСВ :

М(Х)=

Задача 7.Заданы законы распределения дискретных случайных величин X и Y:

X	2	4	6	8		Y	-1	0	3
P	0,4	0,2	0,1	0,3		P	0,5	0,2	0,3

Найти M(Z), если Z=2X-3Y.

Решение.

M(Z)=M(2X-3Y)=M(2X)-M(3Y)=2M(X)-3M(Y)

M(X)=

M(Y)=

M(Z)=

Задача 8. Найти математическое ожидание случайной величины Х, заданной функцией распределения вероятностей

Решение. По определению вычислим f(x):

Используя определение математического ожидания НСВ, получим:

=

.

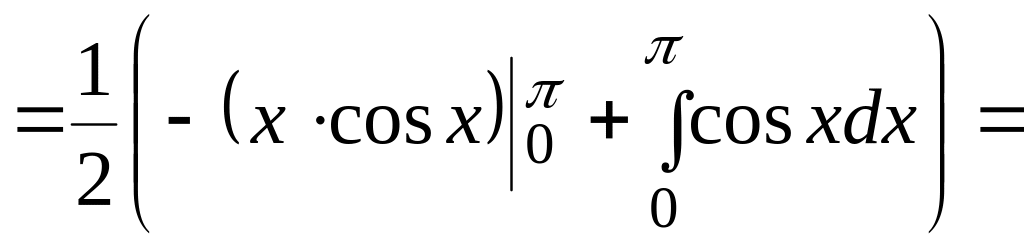
2. Дисперсия случайной величин.

Необходимость введения этой числовой характеристики вызвана тем, что на практике часто встречаются СВ, имеющие равные математические ожидания, но значения одной из них резко отличаются от значений другой, например:

Х	-1	0	1		Х	- 1000	0	1000
Р	0,3	0,4	0,3		Р	0,2	0,6	0,2

М(Х)=М(Y)=0 (проверьте это самостоятельно).

Значения СВ Х более сконцентрированы около математического ожидания, чем значения СВ Y.

Дисперсия – это числовая характеристика, выражающая меру рассеяния значений СВ вокруг математического ожидания.

Определение. Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Обозначение: D(X)

D(X)= .

Определение. Дисперсией непрерывной случайной величины, все значения которой принадлежат [a;b], называют число, определяемое по формуле:

D(X)= – плотность распределения вероятностей.

Замечание. Если значения НСВ X распределены на всей числовой оси, то

D(X)= если интеграл сходится.

Свойства дисперсии.

1. D(С)=0, где C-const.

Дисперсия постоянной величины равна 0.

2. D(CX)= 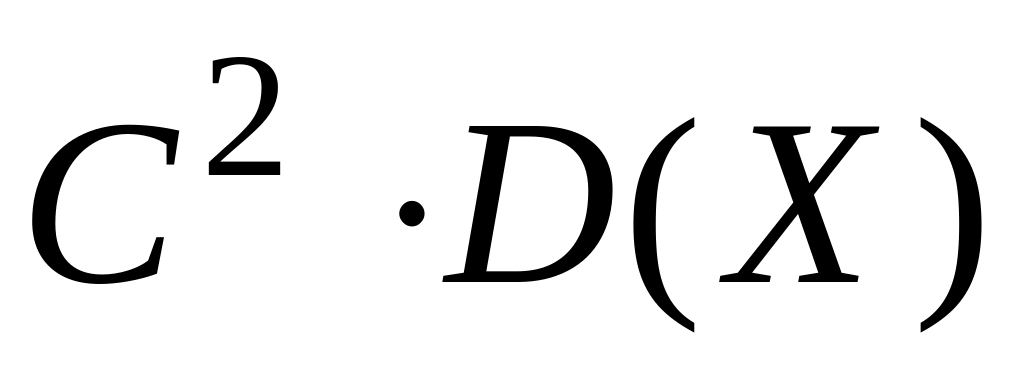, где C-const.

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3. Дисперсия суммы (или разности) двух независимых случайных величин равна сумме их дисперсий.

4. D(X)=

Дисперсия СВ равна разности между математическим ожиданием квадрата СВ и квадратом ее математического ожидания.

Задача 9. Вычислить дисперсию ДСВ Х, заданной законом распределения вероятностей:

Х	0	1	3	5
Р	0,4	0,2	0,1	0,3

Решение.

I способ. Воспользуемся определением дисперсии ДСВ.

X	0	1	3	5
P	0,4	0,2	0,1	0,3
X-M(X)	-2	-1	1	3
(X-M(X))	4	1	1	9

М(Х)=

D(X)= = .

II способ. Для вычисления дисперсии воспользуемся свойством 4.

Х	0	1	9	25
Р	0,4	0,2	0,1	0,3

D(X)= = .

Задача 10. Вычислить дисперсию непрерывной случайной величины Х, заданной функцией распределения вероятностей F(x).

Решение. Найдем плотность распределения вероятностей НСВ Х:

Вычислим M(X) по определению:

I способ. По определению дисперсии НСВ имеем:

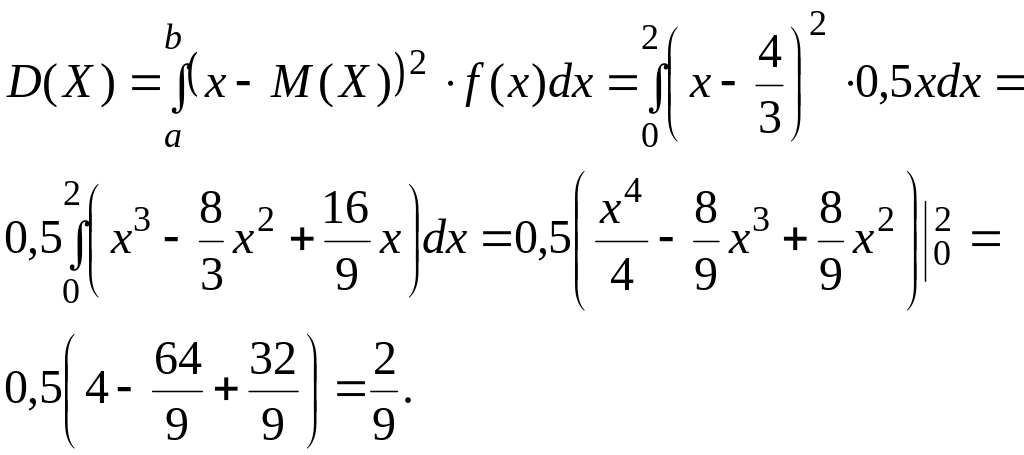
II способ. По свойству 4 :

D(X)= = –

–