3. Порядок выполнения лабораторной работы.

По заданию преподавателя выбрать вариант таблицы содержащей результаты многомерного эксперимента. Ввести предполагаемый вид аппроксимирующего полинома на листе «Вид модели». Рекомендуется проводить исследование и построение модели начиная с полинома первой степени (линейная модель).

На вкладке «Макросы» вызвать программу нахождения параметров модели. По виду модели программно формируется система нормальных уравнений и затем решается одним из методов исследованных в предыдущей лабораторной работе.

На листе «Параметры модели» приводятся значения параметров и оценка средне квадратичной и максимальной погрешности модели выбранного вида. По формулам оценки значимости параметров модели исключить из модели незначимые члены полинома и затем ввести в модель (полином) члены более высоких порядков для снижения погрешности моделирования.

Повторить вышеприведенные операции до получения необходимой точности модели.

Отчет по лабораторной работе должен содержать следующие результаты исследования:

- виды полиномиальных моделей;

- значения погрешностей моделей;

- оценки значимости параметров модели;

- оценки вычислительных затрат.

Лабораторная работа №4 Моделирование процессов в устройствах автоматических систем

1. Цель работы

Целями предлагаемой лабораторной работы является моделирование различных временных процессов в устройствах автоматических систем и получение практических навыков в использовании методов анализа процессов с помощью решения дифференциальных уравнений численными методами.

2. Основные положения методик анализа процессов

Одним из часто используемых элементов автоматических систем является звено второго порядка. Такое звено может быть представлено электрическим аналогом, эквивалентная схема которого приведена на рис. Рассматривая устройство как четырехполюсник в системе G параметров, коэффициент передачи по напряжению будет иметь вид:

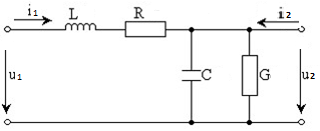
Рис 4.1. Эквивалентная схема

где Z = R + pL; Y = G + pG . Учитывая то, что величина G как правило может быть величиной входной проводимости следующего каскада или проводимостью изоляции в кабельной линии её можно считать близкой к нулю. Тогда коэффициент передачи можно записать в виде

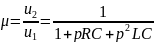(4.1)

и делая замену оператора

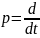
Представим связь между u₁(t) и u₂(t), как модель процесса в виде дифференциального уравнения второго порядка

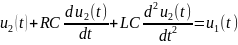(4.2)

Решение полученного уравнения описывает процесс в исследуемом устройстве. Это уравнение приводится к системе уравнений первого порядка для возможности применения численных методов.

Решение систем дифференциальных уравнений

Задача Коши заключается в решении си­стем обыкновенных дифференциальных урав­нений первого порядка, представляемых в виде

……………………………………

……………………………………

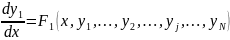
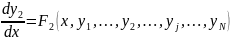
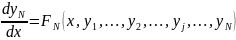
где j=1÷N — номер каждой зависимой переменной у_j,

х — независимая переменная. Если задача Коши решается для анализа поведения системы или объекта во времени, то х является временем (x = t). Решение при заданных начальных условиях х=х₀, у₁ (x₀)=у₀, y₂(х₀)=y₂, …, y_N(x₀)=y_N сводится к нахождению зависимостей (интегральных кривых) у₁ (х), у₂(х),.., у_j (х),...., y_N (х), проходящих через точки, заданные начальными усло­виями (х₀, у₁₀), (х₀, у₂₀), , (х₀, у_j0), …, (х₀, у_N0), Задача Коши сводится к инте­грированию дифференциальных уравнений. Порядок метода численного интегрирования при этом определяет и порядок метода решения.

Обобщенная форма записи каждого из уравнений системы может быть пред­ставлена в общем виде

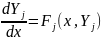
где Y_j в правой части уравнения — векторы переменных

у₁ (х), у₂(х),.. у_j (х),..... y_N (х) а F_j — правая часть каждого из уравнений ()). В частности, одно дифференциальное урав­нение (y=Yj=Yi и F_j = F=F₁) записывается в виде

.

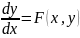Дифференциальные уравнения высшего порядка

(4.3)

где (п) — порядок уравнения, могут быть сведены к системам вида () или () с помощью следующих преобразований:

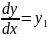
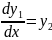
……………. (4.4)

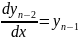
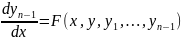
Следовательно, решение (4.3) сводится к ре­шению системы дифференциальных уравне­ний первого порядка( 4.4).

Метод Эйлера — Коши — простейший ме­тод первого порядка для численного инте­грирования дифференциальных уравнений. Он реализуется следующей рекуррентной формулой:

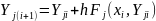(4.5)

где h — шаг интегрирования (приращение переменной х). Этот метод обладает боль­шой погрешностью и имеет систематическое накопление ошибок. Погрешность метода R~(h²) т. е. пропорциональна h².

Метод Эйлера — Коши с итерациями за­ключается в вычислении на каждом шаге начального значения

(4.6)

Затем с помощью итерационной формулы

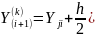(4.7)

решение уточняется. Итерации проводят до тех пор, пока не совпадает заданное число цифр результата на двух последних шагах итераций. Погрешность метода R ~ (h³). Обычно число итераций не должно превы­шать 3—4, иначе нужно уменьшить шаг h.

Модифицированный метод Эйлера второго порядка реализуется следующими рекур­рентными формулами:

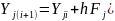(4.8)

где .

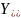Метод дает погрешность R~(h³) и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения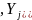

Метод трапеций — одна из модификаций метода Эйлера второго порядка. Он реали­зуется применением на каждом шаге формулы

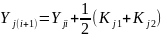(4.9)

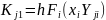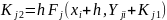где , , и дает погрешность R~(h³). Этот ме­тод относится к общим методам Рунге - Кутта.

Метод Рунге — Кутта четвертого порядка является наиболее распространенным мето­дом решения систем () при шаге h = const. Его достоинством является высокая точность — погрешность R~(h⁵) — и мень­шая склонность к возникновению неустойчи­вости решения. Алгоритм реализации метода Рунге — Кутта заключается в циклических вычислениях Y_j(i+1) на каждом i+1 шаге по следующим формулам:

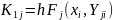
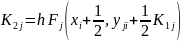
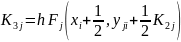(4.10)

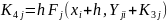
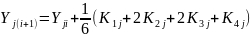
При переходе от одной формулы к дру­гой задаются или вычисляются соответствую­щие значения х и Y_j; и находятся по под­программе значения функций F_j (х, Y_j,).Решение одного дифференциального урав­нения методом Рунге — Кутта производится по приведенным формулам, если в них опустить индекс j, а из алгоритма исклю­чить циклы.. Последнее резко упрощает программу и позволяет получить минималь­но возможное время счета.

Ввиду особого значения и широкого при­менения дифференциальных уравнений вто­рого порядка полезно иметь специальную программу для их решения.

Метод Рунге — Кутта для дифферен­циального уравнения второго порядка вида

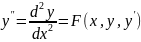(4.11)

имеющий погрешность R~(h⁵), реализуется с помощью следующих формул:

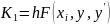
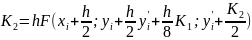
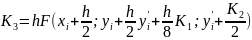
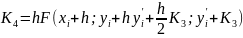(4.12)

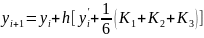
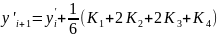
Перед началом вычислений надо задать шаг h и начальные значения х_о, у(х_о)=у_о и у' (х₀) =y₀′.

Автоматическое изменение шага в ходе решения систем дифференциальных уравне­ний необходимо, если решение требуется получить с заданной точностью. При высо­кой точности (погрешность ε=E=10^-3) и решении в виде кривых с сильно разли­чающейся крутизной автоматическое измене­ние шага обеспечивает уменьшение общего числа шагов в несколько раз, резко умень­шает вероятность возникновения числовой неустойчивости, дает более равномерное рас­положение точек графика кривых (решений) при их выводе на печать.

Метод Рунге — Кутта с автоматическим изменением шага заключается в том, что после вычисления y_j(i+1) с шагом h все вы­числения проводятся повторно с шагом h/2. Полученный результат y*_j(i+1) сравнивается с y_j(i+1). Если с |y_j(i+1) ̶ y*_j(i+1)|<е, вычис­ления продолжают с шагом h, в противном случае шаг уменьшают. Если это неравен­ство слишком сильное, шаг, напротив, увели­чивают. При той же погрешности R~(h^s) лучшие результаты дает описанный ниже метод.

Метод Рунге — Кутта — Мерсона с авто­матическим изменением шага обеспечивает приближенную оценку погрешности на каж­дом шаге интегрирования. Погрешность интегрирования имеет порядок п⁵. Этот метод реализуется следующим алго­ритмом.

1. Задается число уравнений N, погреш­ность ε= Е. начальный шаг интегрирования h = H и начальное значение х=х₀, у₁ (x₀)=у₀, y₂(х₀)=y₂, …, y_N(x₀)=y_N

2. С помощью 5 циклов с управляющей переменной j= 1, 2, ...., N вычисляются коэф­фициенты:

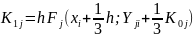
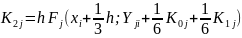
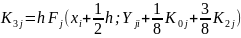
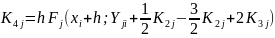
3. Находятся (в последнем цикле) зна­чение

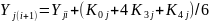
и погрешность

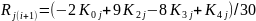
4. Проверяется выполнение условий

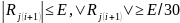
Если первое условие не выполняется, де­лится шаг h на 2 и повторяются вычисления с п. 2, восстановив начальные значения Y_ji. Если это условие выполняется и выпол­няется второе условие, значения x_i+1=x_i+h выводятся на печать. Если второе условие не выполняется, шаг h увеличи­вается вдвое и вычисления опять повто­ряются с п. 2.

Таким образом, Y_j(i+1) выводится на пе­чать только при одновременном выполнении условий этого пункта.

Как отмечалось, погрешность R_j(i+1) на каждом шаге метода Рунге — Кутта — Мер­сона оценивается приближенно. При решении нелинейных дифференциальных уравнений истинная погрешность может отличаться в несколько раз от заданной E.

Метод Рунге — Кутта — Фельберга с ав­томатическим изменением шага дает более точную оценку погрешности на каждом шаге и реализуется последовательным цикличе­ским вычислением по следующим формулам :

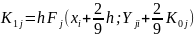
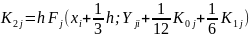
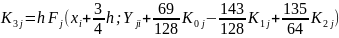
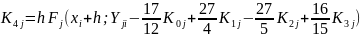
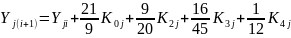
Погрешность

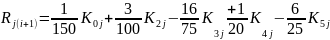
в этом методе — разность приращений Y_j(i+1), вычисленных по двум формулам: порядка n = 4 () и порядка n+1. Последняя формула не приводится, но использована для вычисления R_j(i+1) Если R_j(i+1) >E, шаг n уменьшается вдвое, если R_j(i+1) < E/20, он увеличивается вдвое. Этот метод имеет четвер­тый порядок.

Одношаговые методы решения систем дифференциальных уравнений, к которым от­носятся все описанные выше методы, осно­ваны на вычислениях по рекуррентным фор­мулам, содержащим данные, полученные из решения на одном предшествующем шаге. Эти методы обеспечивают автоматическое начало вычислений при заданных началь­ных условиях и изменение (в том числе автоматическое) шага в ходе вычислений.

Многошаговые методы решения диффе­ренциальных уравнений базируются на ис­пользовании данных решения на нескольких предшествующих шагах. Это позволяет повысить скорость вычислений. Однако для начала вычислений приходится выполнять одношаговыми методами несколько первых шагов. Аналогично это делается при каж­дой смене шага интегрирования.

Методы прогноза и коррекции — разно­видности многошаговых методов, при кото­рых решение вначале проводится по формуле прогноза, а затем уточняется по формуле коррекции.

Ввиду сложности программной реализа­ции многошаговых методов, а также неявных методов численного интегрирования (послед­ние лишены численной неустойчивости реше­ния), они редко используются при решении задач на персональных ЭВМ.