II Оценка точности

8. Вычисляются величины поправок по формуле или .

9. Определяется произведение .

10. Вычисляется суммарное значение .

11. Получается средняя квадратичная погрешность единицы веса

12. Контролируется значение средней квадратичной погрешности единицы веса по формуле , где - коэффициент пропорциональности, принятый при определении весов измерений.

13. Определяется средняя квадратичная погрешность М надежного значения искомой величины по формуле .

14. Проверка выполнения контрольного соотношения: .

III Представление результата обработки неравноточных измерение одной величины в виде

Теперь рассмотрим пример обработки равноточных измерений одной величины.

Пример (взят из [1]). Одна и та же линия измерена светодальномером 15 раз в разное время, разным числом приемов. Принимая веса отдельных измерений пропорциональными числу приемов, найти надежное значение длины линии и её среднюю квадратичную погрешность.

Таблица 2

Результаты измерений

i	, м	Количество приемов,
1	736,30	6
2	736,25	6
3	736,37	10
4	736,48	5
5	736,26	10
6	736,48	10
7	736,39	6
8	736,37	10
9	736,36	12
10	736,48	3
11	736,50	12
12	736,52	6
13	736,37	6
14	736,40	6
15	736,50	3

Проведение вычислений

I Определение надежного значения измеренной величины (округленного значения среднего арифметического искомой величины).

Вычисляем веса измерений и их суммарное значение . В качестве приближенного значения длины линии принимаем наименьшее значение, т.е. «условный ноль» . Вычисляем отклонения по формуле . Затем найдем суммарное значение всех отклонений, умноженных на соответствующие веса , а так же его среднее . Тогда, надежное значение измеренного угла будет .

II Оценка точности.

Вычисляем поправки и определяем квадраты этих поправок, умноженные на соответствующие веса их суммарное значение . Теперь получим среднюю квадратичную погрешность единицы веса по формуле .

Определим среднюю квадратичную погрешность М надежного значения искомой величины по формуле .

Теперь проверим выполнение контрольного соотношения:

782,97=3115,3-160,9²/11,1

782,97=782,97.

III Представление результата обработки неравноточных измерение одной величины в виде .

Окончательно результат обработки равноточных измерений угла будет (736,3950,022)м.

Выполнение расчета в Excel

Пример выполнение в Excel обработки равноточных измерений одной величины представлен на рисунке 1.

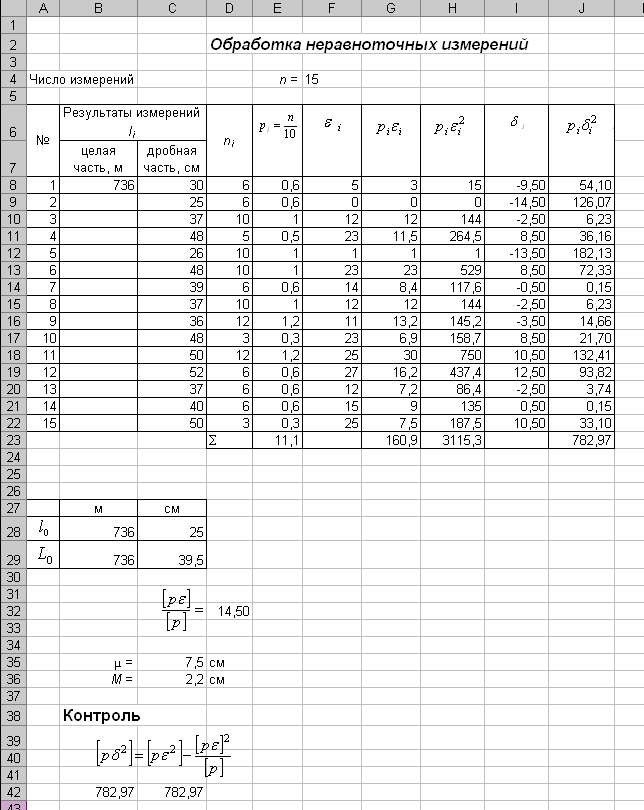
Рис. 1. Пример проведения расчета в Excel

По полученным результатам можно сделать вывод:

Окончательный результат определения угла будет: (736,3950,022)м. Результаты, полученные «вручную» и в Excel совпадают. При проведении вычислений все проверки сошлись.