4.2. Таблица истинности для логического элемента «или»:
Правило: результат равен , если все операнды равны ; во всех остальных случаях результат равен .
Т |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аблица
истинности
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
"1" тогда и только тогда, когда хотя бы на одном входе есть «1»,
"0" тогда и только тогда, когда на всех входах «0»
4.3. Таблица истинности для логического элемента «не» (схема инверии):
И
нвертор
A |
|
0 |
1 |
1 |
0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
"1" тогда и только тогда, когда на входе «0»,
"0" тогда и только тогда, когда на входе «1»
4.4. Инверсия функции конъюнкции. Операция 2и-не (штрих Шеффера)
2
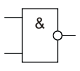И-НЕ
A |
B |
f(AB) |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
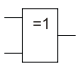
4.5. Инверсия функции дизъюнкции. Операция 2или-не (стрелка Пирса)
2
ИЛИ-НЕ
A |
B |
f(AB) |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
"1" тогда и только тогда, когда на всех входах действуют «0»,
"0" тогда и только тогда, когда хотя бы на одном входе действует «1»
A |
B |
f(AB) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
4.7. Элемент памяти на основе триггера
Триггер- элементарная ячейка памяти,
имеет два устойчивых состояния 0 и1.
Наличие 0 и1 на выходах
определяются в зависимости от комбинации
входных сигналов S (set –
установка уровня сигнала на выходе
в 1) и R ( reset – сброс в 0). Различают
T-григгеры, RS- триггеры, JK триггеры, D-
триггеры, T –триггеры.
Все триггеры разделяют на асинхронные
и синхронные (переключаются при наличии
синхронизирующих импульсов).
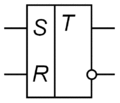
Условное графическое обозначение асинхронного RS-триггера:
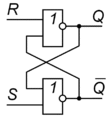
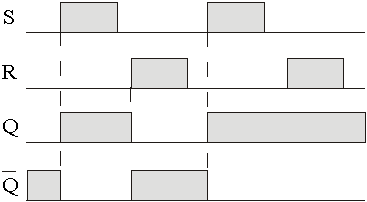
Условное графическое обозначение и временные диаграммы синхронного RS-триггера:
|
|
|
Задача №4 Вписать недостающее логическое выражение в 3-ем столбце.
А B C |
A V B |
? |
0 0 0 |
0 |
1 |
0 0 1 |
0 |
1 |
0 1 0 |
1 |
0 |
0 1 1 |
1 |
0 |
1 0 0 |
1 |
0 |
1 0 1 |
1 |
0 |
1 1 0 |
1 |
0 |
1 1 1 |
1 |
0 |
Решение:
( A V B
) или
Задача № 5 Упростить логическое
выражение
Решение:
Задача № 6 Данной схеме соответствует логическая функция …..
Р
ешение:
В соответствии с требованиями единой
системы конструкторской документации
(ЕСКД) схема имеет вид:
Задача № 7 Поставить соответствующий знак в выражении (X& X) ? (Y& Y), чтобы оно было тождественно истинному.
Решение: Каждое из выражений (в правой и левой скобке ) всегда равно 0, поэтому здесь можно поставить как знак &, так и . То есть при любом знаке между скобками F=0.
З
адача
№ 8 Логическое выражение НЕ ((
Y>4) ИЛИ (Y<1)) И
(Y=2) истинно, когда значение переменной
Y равно …..?
Решение:
Интервал значений от 1 до 4 соответствует
левой части исходного логического
выражения, то есть
=
В этом же интервале находится значение
Y=2. Тогда с учетом того, что операция
«И» соответствует пересечению множеств,
следует решение : Y=2