3. Примеры решения задач на вычисление объема сообщения

и количества информации

Задача № 1: Имеется сообщение объемом 2²³ бит. В мегабайтах объем этого сообщения равен …?

Решение : 2²³ = 2^10+10+3 = 2¹⁰ × 2¹⁰ × 2³ = 2 Mб

Здесь 2¹⁰ × 2¹⁰ = К × К= M ; 2³= 1 б

Задача № 2 : Количество информации в слове «Информатика» при условии, что используется 32-значный алфавит, равно _____ бит.

Решение: Количество информации в n-разрядном слове определяется по формуле Хартли Здесь n=11, q=32 Тогда

Задача № 3 : В конкурсе участвовали 20 студентов, 8 школьников, 4 учащихся колледжа. Количество информации в сообщении о том, что победил школьник, считая, что победа любого участника равновероятна, составит ____ бит.

Решение: Вероятность определяется по формуле

Тогда количество информации определим по формуле Хартли:

Задача № 4 : В текстовом файле хранится текст объёмом 400 страниц. Каждая страница содержит 3200 символов. Определить размер файла, если используется кодировка символов ASC-II (8 бит на 1 символ). Варианты ответов: 1280 Кб; 1 Мб; 1250 Кб; 1,28 Мб.

Решение: . Так как в таблице ASC-II один символ обозначается словом разрядностью 8 бит, т.е. одним байтом, то объём файла равен байт. Определим размер файла в Кб, воспользовавшись переводным коэффициентом 1024 (а не 1000), тогда .

4. Элементарные основы булевой алгебры (алгебры логики). Примеры построения логических схем на элементах интегральной логики

Логика высказываний (или пропозициональная логика от англ. propositional logic) — это формальная теория, основным объектом которой служит понятие логического высказывания. Алгебра логики создана английским математиком Джоржем Булем (1815-1864) и предназначена для выполнения логических операций с двоичными числами. На ее основе выполнены логические схемы современных ЭВМ. Алгебра логики или алгебра высказываний — раздел математической логики (бинарная или двоичная логика), в котором изучаются логические операции над высказываниями, при этом полагается, что высказывания могут быть только истинными или ложными. Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B, , , , 0, 1}, где B — непустое множество, над элементами которого определены три операции:

отрицание («НЕ») ; дизъюнкция («ИЛИ») ; конъюнкция («И») .

Константы: логический ноль 0 и логическая единица 1. Далее в примерах под знаками «плюс» и «умножить» следует понимать логическое сложение (дизъюнкцию) и логическое умножение (конъюнкцию). Логика высказываний является простейшей логикой, максимально близкой к человеческой логике неформальных рассуждений и известна ещё со времён античности.

Знаки и (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками.

Подформулой называется часть формулы, сама являющаяся формулой.

Собственной подформулой называется подформула, не совпадающая со всей формулой.

Тождественно истинной называется формула , если она истинна при любых значениях входящих в неё переменных.

Вот несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

1) ;

2 ) ; или

Закон контрапозиции:

;

Законы поглощения:

1) ;

2) ;

Законы дистрибутивности:

1) ;

2) .

Оценка отрицания задаётся таблицей:

Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация А→B  — это сокращённая запись для выражения .

Значение двуместных логических связок (импликация), (дизъюнкция) и (конъюнкция) определяются так:

0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	1	1	1

АКСИОМЫ:

1. (операция двойного отрицания или двойной инверсии)

2. (операция логического сложения или дизъюнкции xV x =1)

3. 

4. 

5. 

6. 

7. 

8. 

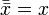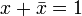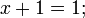
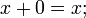
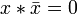
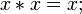
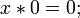
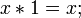9. (операция логического умножения или дизъюнкции x 1 =1 или x &1=1)

4.1. Таблица истинности для логического элемента «И» (схема совпадения):

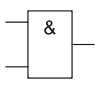
• "1" тогда и только тогда, когда на всех входах есть «1»,

• "0" тогда и только тогда, когда хотя бы на одном входе есть «0»