5.4. Проверочный расчет зубьев на выносливость при изгибе и на контактную выносливость

При проектировании зубчатых передач обычно выполнятся два типа расчетов – проверочный и проектировочный. В локомотивостроении проектировочный расчет, как правило, не проводится, поскольку основные размеры передачи определяются из условия ее вписывания в заданный монтажный объем.

Целью проверочного расчета передачи при известных размерах и нагрузках является определение ее нагрузочной способности. В процессе проверочных расчетов зубьев на выносливость производится определение расчетных напряжений и их сравнение с допустимыми.

Для ведущих и ведомых зубчатых колес тяговых передач приняты допустимыми следующие расчетные напряжения [ ]. При изгибе: шестерня – МПа; колесо – МПа. Контактные напряжения: шестерня – МПа; колесо – МПа.

Напряжения при расчете зубьев передачи на выносливость при изгибе определяются по формуле:

;

где: – коэффициент формы зуба определяется по графику (рис. 5.12) в зависимости от числа зубьев и выбранных коэффициентов смещения; – коэффициент перекрытия зубьев; – коэффициент наклона зубьев, для прямозубой передачи ; – модуль зацепления; – удельная расчетная нагрузка действующая на головку зуба, Н/мм.

Удельная нагрузка на головку зуба определяется по формуле

;

где: – коэффициент неравномерности распределения нагрузки между зубьями, для прямозубой передачи ; – коэффициент неравномерности распределения изгибных напряжений по длине зуба, для прямозубых тяговых передач ; – коэффициент внутренних динамических нагрузок, в соответствии с [ ] ; – окружная сила в зацеплении, Н; – ширина зубчатого венца, мм.

Окружная сила в зацеплении прямозубой цилиндрической передачи рассчитывается по формуле:

;

где: – крутящий момент подведенный к шестерне, Н/м; – делительный диаметр шестерни, м.

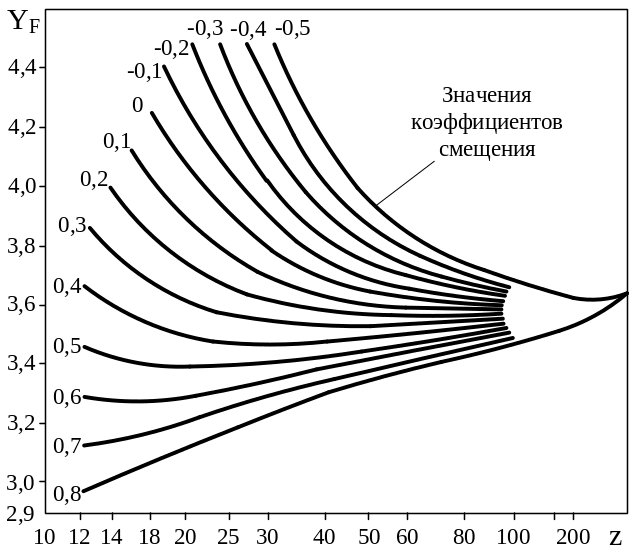
Рис. 5.12. График для определения коэффициента Y_F

Контактные напряжения в зацеплении рассчитываются по формуле:

;

где: – коэффициент формы зуба при расчете на контактную выносливость, определятся по графику (рис. 5.13, а) в зависимости от угла наклона зубьев и отношения суммы коэффициентов смещений к сумме чисел зубьев; – коэффициент суммарной длины контактных линий определяется по графику (рис. 5.13, б) в зависимости от значений коэффициентов торцевого и осевого перекрытий (для прямозубой передачи ); – начальный диаметр шестерни, мм; – передаточное отношение; – удельная нагрузка на середину зуба, Н/мм.

Удельная нагрузка, действующая на середину зуба, определяется по формуле:

;

где: – коэффициент неравномерности распределения нагрузки между зубьями, для прямозубой передачи ; – коэффициент неравномерности распределения контактных напряжений по длине зуба, для прямозубых тяговых передач ; – коэффициент внутренних динамических нагрузок, для прямозубых тепловозных передач .

а) б)

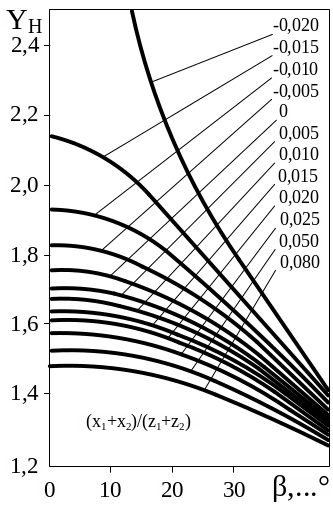
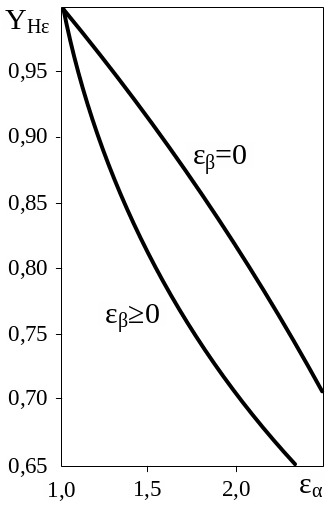
Рис. 5.13. Графики для определения коэффициента формы зуба при расчете на контактную выносливость (а) и коэффициента

суммарной длины контактных линий (б).

Полученные в результате расчета величины , необходимо сравнить с допускаемыми значениями , . Если условия прочности и выполняются, передача является работоспособной по условиям изгибной и контактной выносливости зубьев.