Теория активаторного процесса стирки
На процесс стирки в активаторных стиральных машинах наряду с химическим воздействием моющих средств и температуры воды большое влияние оказывает механическое воздействие потока моющего раствора. В результате загрязнитель отделяется от ткани и уносится потоком воды.
Так как положение кома ткани в процессе стирки непрерывно изменяется, то гидродинамический процесс в стиральном баке представляет собой сложное движение, называемое перемешиванием. При этом в баке возникают два основных режима течения жидкости: ламинарное и турбулентное. Ламинарным называют гидродинамический режим, при котором элементарные частицы жидкости двигаются параллельно в направлении движения потока. Турбулентным называют гидродинамический режим, при котором возникают вихри, хаотически перемещающиеся в объеме движущейся жидкости. Если в ламинарном потоке из одного слоя в другой переходят только молекулы, то в турбулентном – элементарные массы жидкости. Поэтому для получения наибольшей эффективности с точки зрения отстирываемости необходимо создавать турбулентное движение.
В гидродинамике движение жидкостей описывают основным уравнением движения жидкости (уравнение Бернулли):
,
где
– потенциальная энергия положения
элементарной частицы жидкости;
– потенциальная энергия давления
жидкости;
– кинетическая энергия элементарной
точки жидкости.
Если в трубопроводе установившийся процесс, то в единицу времени протекает одна и та же масса жидкости, которую определяют по уравнению непрерывного потока:
,
где
и
– сечения трубопровода;
и
– массовые скорости в сечениях
трубопровода;
и
– плотности жидкости.
Исходя из этих уравнений можно сделать вывод, что при установившемся режиме движения массовые и энергетические характеристики для любого сечения трубопровода остаются постоянными.
При движении реальной жидкости необходимо учитывать потери энергии на преодоление трения и других сопротивлений. В этом случае уравнение Бернулли преобразовывают в выражение, характеризующее изменение напоров:
,
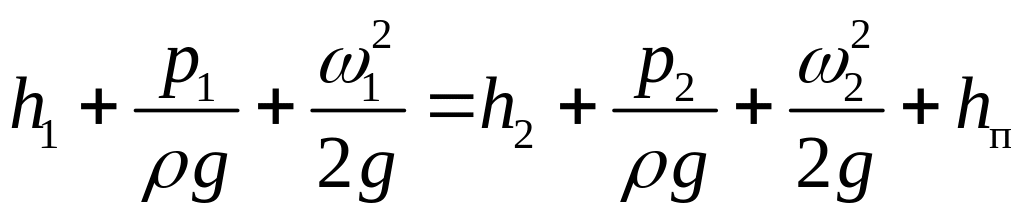где
и
– геометрические напоры, определяемые
высотой столба жидкости над рассматриваемой
точкой;
и
– пьезометрический и скоростной
напоры в разных точках;
– потери напора.
Пользуясь уравнением Бернулли, . определяют скорость, расход жидкости, напор, временные характеристики и другие параметры. Кроме того, из этих уравнений следует, что одинаковые условия течения жидкости можно создать в разных (например по размерам) установках. Условия, необходимые для создания подобных процессов, излагаются в теории подобия. Так, условием подобия двух змеевиков является соблюдение двух равенств:
и
где
,
– длина труб;
,
– радиусы змеевиков;
,
– диаметры труб.
Имеется ряд чисел (критериев) подобия, названных именами ученых, сделавших большие открытия в гидродинамике и теплотехнике.
Критерий Нуссельта
определяет интенсивность конвективного
теплообмена на границе стенка –
жидкость. Чем интенсивнее происходит
теплообмен, тем больше число
и тем больше коэффициент теплоотдачи:
,
где – площадь, в границах которой происходит теплообмен; – теплопроводность жидкости.
Критерий Рейнольдса
определяет характер движения жидкости:
,
где
– средняя скорость жидкости;
– кинематическая вязкость жидкости.
Для стиральных машин критерий Рейнольдса может быть записан в виде:
,
где
и
,
– плотность и вязкость стирального
раствора;
– угловая скорость активатора;
– частота вращения активатора;
– диаметр активатора.
Экспериментальные
исследования показали, что при
обеспечивается интенсивное трехмерное
движение жидкости, а при
– турбулентное движение, при котором
мгновенно изменяется скорость отдельных
частиц и ее направление, т. е. происходит
пульсация скорости. Именно этот режим
благоприятен для стирки.
При вращении активатора в стиральном баке цилиндрической формы возникают три основных потока моющего раствора (Рис. 98): осевой , направленный по оси вращения активатора, радиальный , направленный по радиусу активатора и тангенциальный , направленный по касательной и окружности активатора.
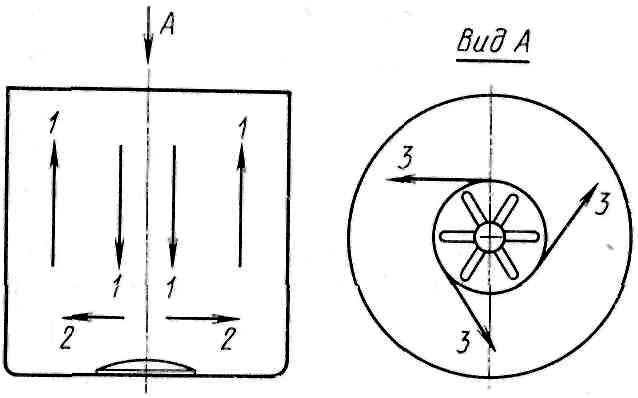
Рис. 98. Схема движения жидкости в стиральном баке с осесимметричным расположением активатора
При установившемся
процессе вращения активатора в жидкости
вокруг оси активатора возникает
однородный цилиндрический вихрь
круглого сечения с постоянной угловой
скоростью (зона
,
Рис. 99). Теоретический диаметр вихря
должен быть равен диаметру
активатора. Скорость частиц в вихре
вдоль радиуса активатора возрастает
линейно. Вне активатора цилиндрический
вихрь возбуждает движение частиц
жидкости вдоль линии радиуса с убывающей
скоростью (зона
).
Между этими двумя зонами возникает
переходная зона
(радиус этой зоны
).
Радиус вихря определен экспериментально:
.
Для потокообразования
первостепенное значение имеет
тангенциальная составляющая.
Тангенциальная скорость в вихре
(где
– угловая скорость жидкости).
В периферийной зоне приближенно можно считать:
в переходной зоне :
.
Тангенциальная скорость достигает своего максимума при:
.
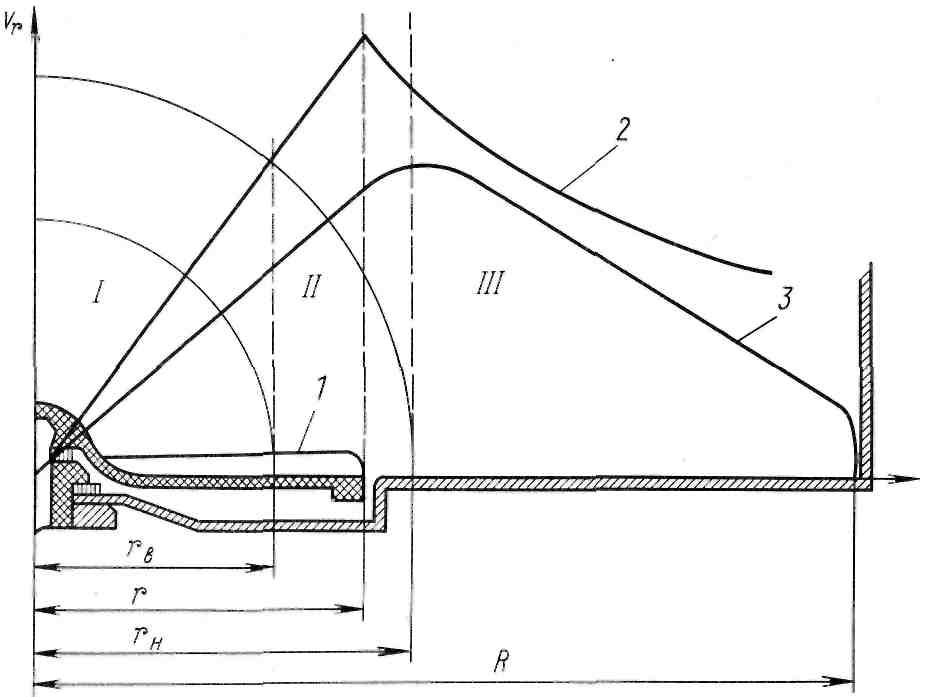
Рис. 99. Распределение скоростей движения частиц раствора в стиральном баке:
– зона цилиндрического однородного вихря; – переходная зона; – зона падающей скорости; – активатор; – теоретическое распределение скоростей; – реальное распределение скоростей
Наличие радиальной скорости жидкости на дне бака у активатора создает повышенное давление у стенки бака и разрежение в центре. Таким образом, возникает восходящий поток у стенки и ниспадающий в центре активатора. При определенных скоростях по оси вращения может образовываться воронка, которая значительно ухудшает условия трехмерного перемешивания.
Характер циркуляции зависит от соотношения размеров активатора и бака, частоты вращения активатора, а также от его формы (Рис. 100). Как видно, в любом случае с осесимметричным активатором имеются условия для образования воронки. Воронка нарушает структуру потока и ткань концентрируется под нею. С увеличением глубины воронки ткань прижимается к активатору и практически не перемешивается. На Рис. 101 показана зависимость глубины воронки от частоты вращения при различных размерах активатора и отражательных элементов.
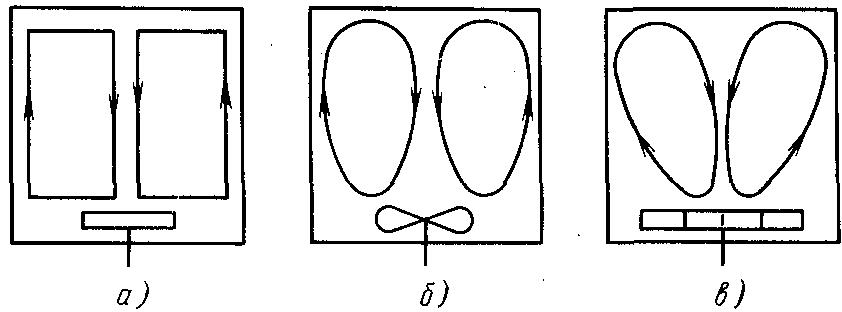
Рис. 100. Образование потока при различных формах активатора:
а – диск с вертикальными лопастями; б – активатор вертикального типа; в – турбинный активатор
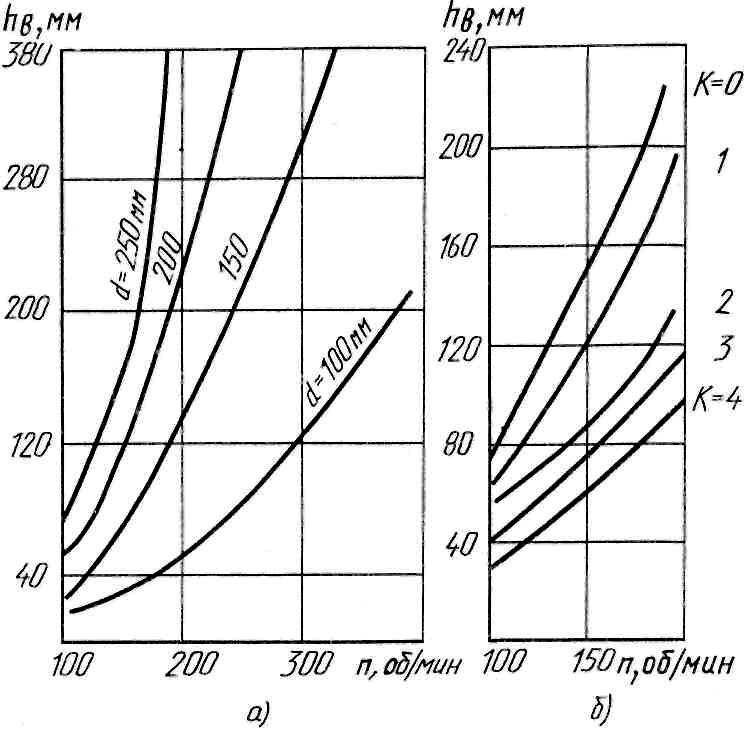
Рис. 101. Зависимость глубины воронки:
а – от частоты вращения активатора; б – от частоты вращения активатора при различном числе отражательных элементов на баке
Для уменьшения воронки применяют различного вида отражательные элементы, которые создают локальные завихрения по периметру бака. Однако отражательные элементы увеличивают сопротивление потока, что приводит к увеличению потребляемой мощности. На Рис. 102 видно, что уменьшение глубины воронки в 2 раза ведет к увеличению потребляемой мощности также в 2 раза. Кроме того, при плоском дне бака потребляемая мощность больше, чем в машинах с полуцилиндрическим или сферическим дном. При увеличении высоты жидкости над активатором потребляемая мощность также увеличивается.
Поэтому стараются не использовать осесимметричное расположение активатора, а применять боковое его расположение или несколько активаторов (Рис. 103).
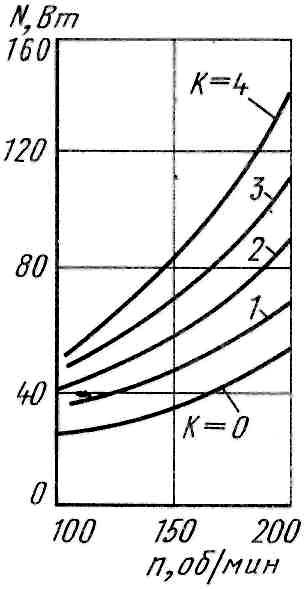
Рис. 102. Зависимость потребляемой мощности от частоты вращения активатора при различных количествах отражательных элементов на баке
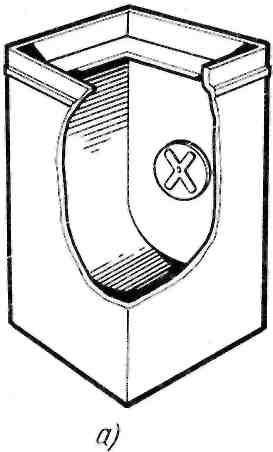
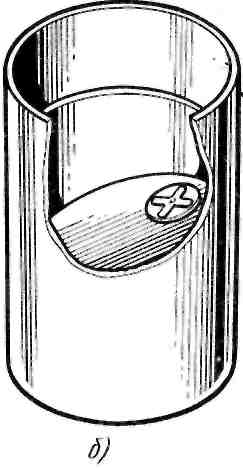
Рис. 103. Несимметричное расположение активатора:
а – боковое; б – наклонное
По экспериментальным данным перегородки на крышке бака повышают отстирываемость на 6– 9%. Кроме этого, применение ребер в крышке дает возможность ликвидировать воронку при меньших затратах мощности, чем при установке их на внутренней поверхности бака. Оптимальной высотой ребер на крышке является такая, при которой, если отсутствует активация, ребра касаются поверхности раствора.
В машинах с цилиндрическим баком активатор располагают наклонно, в машинах с прямоугольным баком – сбоку. Осесимметрично располагают активатор в машинах с несимметричным баком, что уменьшает воронкообразование, а также в машинах, в которых стиральный бак совмещен с центрифугой.