Динамика перемещения ткани во вращающемся барабане
Процессы
стирки и полоскания в машинах барабанного
типа основаны на принципе динамического
взаимодействия материальных систем,
участвующих в относительном движении
барабана. На каждую материальную точку
белья массой
(Рис. 94)
действуют силы: центростремительная,
тяжести и инерции. В совокупности все
эти силы определяют направление и
характер движения данной материальной
точки. Отношение центробежной силы
к силе тяжести
характеризуется критерием Фруда
(фактором разделения):
,
где
- угловая скорость вращения барабана;
– расстояние от оси вращения до
материальной точки.
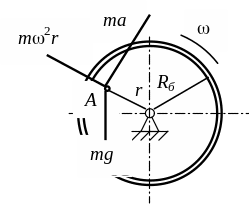
Рис. 94. Силы, действующие на материальную точку во вращающемся барабане
Материальная точка массой приобретает относительное движение в барабане в сторону результирующего ускорения:
.
Движение
материального потока (раствора и белья)
зависит от угловой скорости барабана.
Условно выделяют четыре режима [20]:
лавинообразный
при
(Рис. 95, а),
лавиноводопадный
при
(Рис. 95, б),
водопадный
(критический) при
(Рис. 95, в)
и закритический
при
(Рис. 95, г).
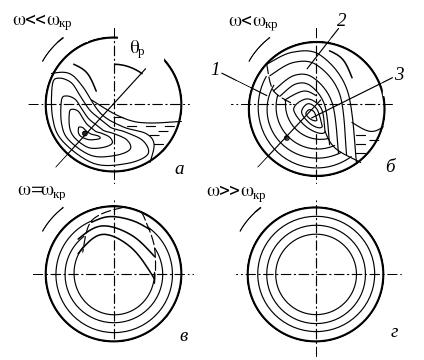
Рис. 95. Режимы движения материального потока при различных частотах вращения барабана:
а – лавинообразый; б – лавиноводопадный: 1 и 2 – восходящая и нисходящая ветви потока;
3 – разграничивающая зона; в – водопадный; г – закритический
Для стирки, полоскания задают лавиноводопадный режим движения. Он характеризуется тем, что в определенных точках пространства барабана происходит отделение частей белья и моющего раствора от общей массы и падение их в другую часть барабана. При этом происходит трение белья друг о друга, удар его о поверхность моющего раствора и интенсивное перемешивание. Различают две части потока: восходящую и нисходящую ветви.
Восхождение потока белья вместе с частью жидкости происходит из левого нижнего квадранта окружности барабана в левый верхний квадрант (Рис. 96).
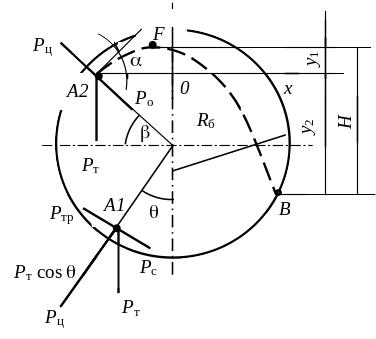
Рис. 96. Движение потока белья
Рассмотрим
движение материальной точки потока
относительно барабана, на поверхности
которого она находится. Сила, стремящаяся
придать точке
скольжение, - составляющая силы тяжести:
,
где
- угол подъема точки в нижнем квадранте.
Силе скольжения противодействует сила трения:
,
где
– коэффициент трения;
- радиус барабана.
Точка
не будет скользить по барабану, пока
,
т.е.
,
или пока не будет достигнуто условие:
Если
барабан неподвижен
,
то
.
Соотнеся
с углом трения
,
получим:
.
Это
означает, что при неподвижном барабане
угол
не может превысить угол трения
.
При вращающемся барабане и подъеме
точки
выше горизонтального диаметра барабана
ее положение будет характеризоваться
углом
.
При этом на точку
перестанет действовать составляющая
силы трения от силы тяжести
.
Если угол
таков, что
,
т.е.
,
то тело в точке
будет падать в нижнюю часть барабана
по параболе как свободное тело, брошенное
со скоростью
под углом к горизонту
.
Угол
называют при этом углом отрыва.
До
наступления отрыва возможно движение
точки с проскальзыванием. Оно наступает,
когда угол
достигает значения, определяемого по
уравнению .
Из-за
различия между коэффициентами трения
движения
и трения покоя
формула дает два значения угла
:
и
соответственно. Это означает, что во
вращающемся барабане точка
поднимается на угол
,
затем начинает скользить вниз до
положения
.
После этого процесс повторяется.
Движение
точки
в
-м
слое восходящего потока происходит
при соответствующих значениях
,
,
и
.
По уравнению можно сделать вывод, что
угол
по слоям восходящего потока – величина
переменная, зависящая от скорости
.
Относительная
скорость скольжения двух смежных слоев
вызывает взаимное трение белья в
процессе стирки и полоскания.
Нисхождение
потока характеризуется падением белья
в нижнюю часть барабана. Траектория
точки
белья
представляет собой кривую
,
состоящую из двух ветвей:
(подъем после отрыва от барабана со
скоростью
)
и
(свободное падение).
Высоту
ветви
можно определить из уравнения движения
тела
,
но
,
следовательно, время падения
,
где
,
– частота вращения и диаметр рабочего
барабана. Учитывая это уравнение,
находим:
.
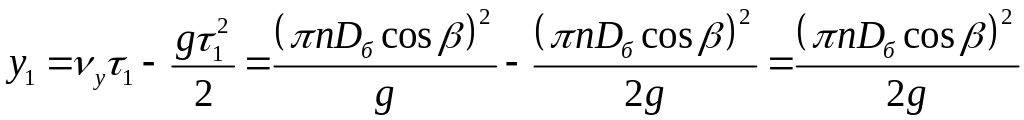Отрыв белья от стенки барабана произойдет в момент, когда составляющая силы тяжести станет равной центробежной силе, т.е.:
.
С учетом данного равенства уравнение примет вид:
После некоторых преобразований найдем координаты точки падения белья:
.
Полная высота падения белья:
.
Величина
достигнет максимума при условии:
0;
;
.
Мощность, необходимую для вращения барабана при стирке и полоскании, можно определить на основе следующей схемы (Рис. 97).
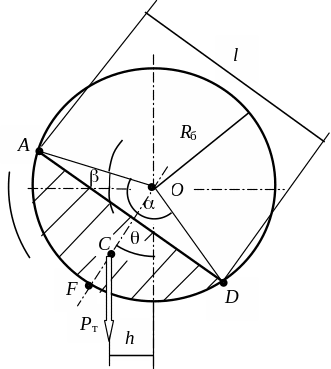
Рис. 97. Схема для определения полезной мощности барабана
Масса белья,
находящегося в жидкости внутри
вращающегося барабана принимает форму,
близкую к форме цилиндрического сегмента
.
Центр тяжести сегмента (точка
)
смещается в сторону вращения. Полезный
момент силы сопротивления вращению
барабана:
,
где
- сила тяжести массы изделий и жидкости
в барабане;
расстояние от оси вращения барабана
до центра тяжести белья и жидкости в
барабане;
- угол поворота сегмента.
Масса мокрого белья в барабане:
,
где
- масса сухого загружаемого белья;
- масса жидкости, впитанной бельем (для
воды и водных моющих растворов в тканых
изделиях
.
Масса жидкости, увлекаемой бельем при вращении барабана:
.
Общая масса
.
Объем, занимаемый мокрым бельем и свободной жидкостью:
,
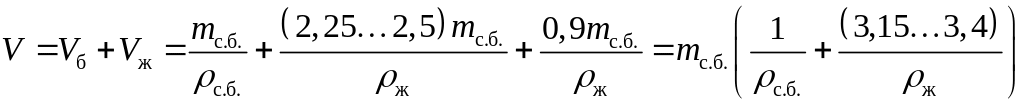где
- плотности сухого белья и жидкости
соответственно.
Обычно принимают
.
Тогда
Положение центра тяжести сегмента находится из геометрических соотношений:
,
где - длина хорды сегмента; - площадь сегмента.
Площадь сегмента
- это часть площади поперечного сечения
барабана
,
где
- длина барабана.
Длина хорды
связана с центральным углом сегмента
через радиус барабана
:
,
а угол
находится из соотношения:
.
Из формулы получим:
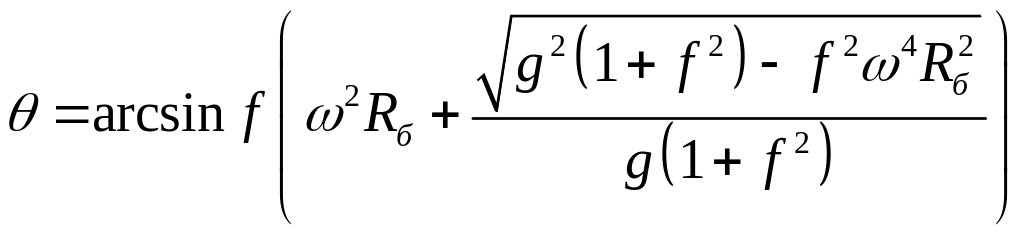
Угловую скорость
следует задавать так, чтобы при
лавиноводопадном режиме обеспечить
наибольшую высоту падения отделившихся
от основной массы частей белья. Этому
соответствует угол отрыва
.
Из соотношений
и
определим оптимальную угловую скорость
барабана при стирке и полоскании:
.
Подставив значения
и других параметров в формулу , определим
.
Мощность на валу барабана для преодоления полезного сопротивления должна составлять:
,
где
– коэффициент, учитывающий неравномерность
полезной нагрузки вследствие падений
и ударов белья внутри барабана
Мощность для преодоления силы трения в подшипниках:
где
– коэффициент трения в подшипниках
(для шарикоподшипников
);
- масса барабана (
,
кг);
- вектор силы натяжения ремня привода
(
Н).
В период пуска барабана необходима дополнительная мощность:
-
на подъем центра тяжести сегмента:
;
-
на преодоление сил инерции масс барабана,
белья и жидкости при разгоне барабана:
,
где
- моменты инерций массы барабана и массы
белья и жидкости
;
);
- время разгона.
Если принять, что разгон барабана совершается за половину оборота, то:
.
Полная мощность при стирке и полоскании:
.