Лабораторная работа №1.2.
Цель работы: Используя 4 варианта элементной базы для представления функции , рассмотренные ранее, построить схему контроля нечетности для 8-ми разрядного кода.
Все этапы выполнения работы №1.2 соответствуют требованиям лабораторной работы №1.1.
Схемы и временные диаграммы входных сигналов и схемы контроля нечетности для 8 разрядов.
1. На элементах И-ИЛИ:
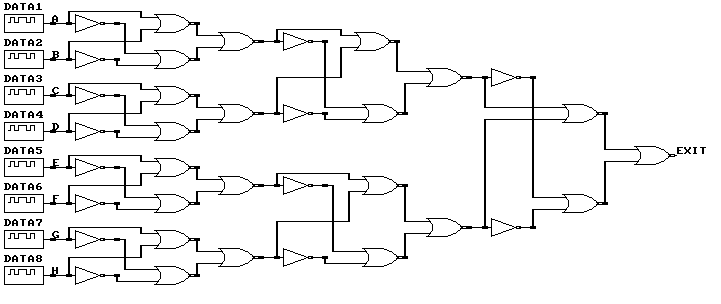
2. На элементах И-ИЛИ-НЕ:
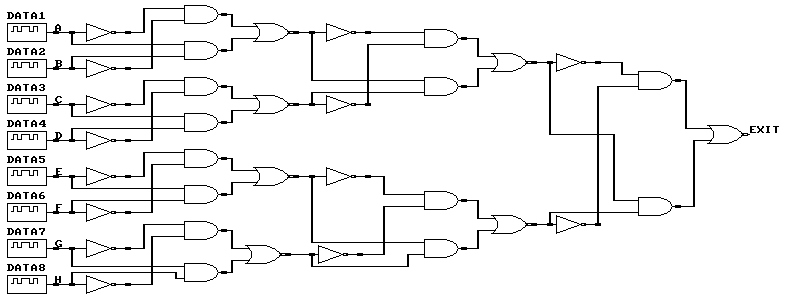
3. На элементах И-НЕ:
4. На элементах ИЛИ-НЕ:
Временные диаграммы:
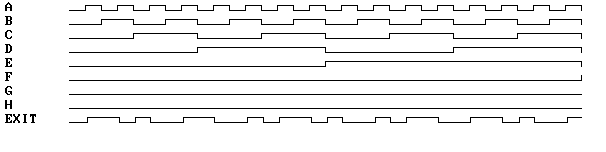
П реобразователи кодов во внешних и внутренних каналах связи в мкс.
ПРi – процессоры.
Гетерогенность источников входной информации, связанная с различными физическими принципами их построения, и необходимость обработки этой информации в одной системе требует наличия во входном интерфейсе внешних преобразователей кодов (ВПК). В зависимости от структуры МКС ее процессоры на аппаратном уровне могут требовать различного кодового представления данных. Преобразователи такого типа относятся к внутренним преобразователям кода. Тип выходных преобразователей определяется структурой исполнительных устройств и будет изучаться в другом разделе.
Наиболее распространенными в МКС являются преобразователи кода Грея, что связано с особенностью построения датчиков в МКС.
Преобразователь кода Грея в простой двоичный код.
Как правило, выходным устройством источника информации, представленной в коде Грея, является матрица следующего вида:
Код Грея называют циклическим двоичным кодом и относят к непозиционным кодам, так как значение любого числа отличается от предыдущего или последующего только значением символа в одном из разрядов. Рассмотрим трехсимвольный код Грея:
Циклический код Грея |
Простой двоичный код |
Эквива- лент |
||||||
G3 |
G2 |
G1 |
B3 |
B2 |
B1 |
|
||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
0 |
0 |
1 |
0 |
0 |
1 |
1 |
||
0 |
1 |
1 |
0 |
1 |
0 |
2 |
||
0 |
1 |
0 |
0 |
1 |
1 |
3 |
||
1 |
1 |
0 |
1 |
0 |
0 |
4 |
||
1 |
1 |
1 |
1 |
0 |
1 |
5 |
||
1 |
0 |
1 |
1 |
1 |
0 |
6 |
||
1 |
0 |
0 |
1 |
1 |
1 |
7 |
||
Синтезировать преобразователь кода Грея в двоичный код с использованием элементной базы М2. Используем метод матриц для получения зависимостей Вi= F(Gi, Вi+1).
-
G3, G2
00 01 11 10
G1
0
0
0
1
1
1
0
0
1
1
B3=G3
-
G3, G2
00 01 11 10
G1
0
0
1
0
1
1
0
1
0
1
-
G3, G2
00 01 11 10
G1
0
0
1
0
1
1
1
0
1
0
Принимая во внимание пункты 1,2,3, возможно для произвольного i-го разряда простого двоичного кода записать соотношение:
Эти выражения являются аппаратной реализацией кода Грея.
Аппаратные затраты на синтезируемый преобразователь определяются разрядностью исходного кода.
N – число разрядов
Минимальные аппаратные затраты приводят к тому что время преобразования входного кода не отвечает режиму реального времени.