2.4. Контрольные вопросы

1. Каким образом могут быть математически описаны случайные погрешности измерений?

2. Какие существуют численные характеристики законов распределения случайных погрешностей? Что они характеризуют?

3. Какие предъявляются требования к оценкам результатов и погрешностей измерений?

4. Какие существуют виды оценок погрешностей результатов измерений?

5. Как рассчитываются оценки математического ожидания, СКО, дисперсии?

6. Какие значения доверительной вероятности при расчёте границ результата рекомендуется принимать? От чего это зависит?

7. Какая величина принимается в качестве результата измерений с многократными наблюдениями?

8. Для чего выполняется проверка подчинения наблюдений нормальному закону распределения?

9. Для чего используются критерии согласия?

10. Как определить уровень значимости критерия? В чём смысл этого понятия?

2.5. Требования к содержанию отчёта

Отчёт по лабораторной работе должен содержать: название лабораторной работы; цель лабораторной работы; схему исследуемой модели с указанием её параметров; массивы неисправленных и исправленных данных; значения всех рассчитанных оценок (с указанием расчётных формул); гистограмму распределения; расчёты по критерию Пирсона, сведённые в таблицу; вывод по работе с записью результата измерения.

3. Лабораторная работа № 3. Косвенные измерения.

Цель работы. Изучение методики обработки результатов косвенных измерений.

3.1. Теоретическая часть Обработка результатов косвенных измерений

При выполнении косвенных измерений задача обработки их результатов заключается в определении оценки искомой величины (функции косвенного измерения) и её погрешности на основании известной зависимости между нею и величинами, функционально, связанными с ней (аргументами косвенного измерения) при известных оценках аргументов и их погрешностей. Уравнение косвенного измерения имеет вид:

, (3.1)

где: X – функция косвенного измерения;

x₁; x₂; … x_m – аргументы косвенного измерения.

Оценку результата косвенного измерения получают путём подстановки в уравнение измерения (3.1) оценок аргументов:

, (3.2)

где – оценки аргументов.

При получении оценок погрешностей результатов косвенных измерений следует различать уравнения линейного и нелинейного вида.

Линейные уравнения косвенных измерений

Линейное уравнение косвенного измерения имеет вид:

, (3.3)

где a_i – числовые константы, принимаемые известными точно (без погрешностей).

Суммарная погрешность результата косвенного измерения определяется по выражению:

, (3.4)

где: _i – оценка систематической погрешности i-го аргумента;

_i – оценка СКО i-го аргумента;

(3.5)

– систематическая погрешность результата косвенного измерения;

(3.6)

– его случайная погрешность.

Оценка СКО случайной погрешности результата косвенного измерения

(3.7)

где _i – оценка СКО i-го аргумента.

Нелинейные уравнения косвенных измерений

Нелинейный характер уравнений косвенных измерений приводит к тому, что закон распределения погрешности результата может существенно отличаться от закона распределения погрешностей аргументов. Оценку погрешности результата при этом выполняют приближённо, путём разложения нелинейного уравнения измерения в ряд Тейлора и отбрасывания членов второго порядка и выше. Оценка систематической погрешности результата измерения при этом определяется по выражению

, (3.8)

где частная производная от уравнения косвенного измерения называется коэффициентом влияния i-го аргумента, а произведение – частной погрешностью.

Оценка СКО случайной погрешности при нелинейном уравнении измерения

, (3.9)

где r_ij – оценка коэффициента парной корреляции между погрешностями i-го и j-го аргументов. На практике определение коэффициента парной корреляции при выполнении косвенных измерений обычно затруднительно, поэтому рассматривают два предельных случая: r_ij = 1 (между погрешностями аргументов существует «жёсткая» линейная связь); и r_ij = 0 (погрешности аргументов некоррелированы). В последнем случае выражение для оценки СКО результата косвенного измерения приобретает более простой вид:

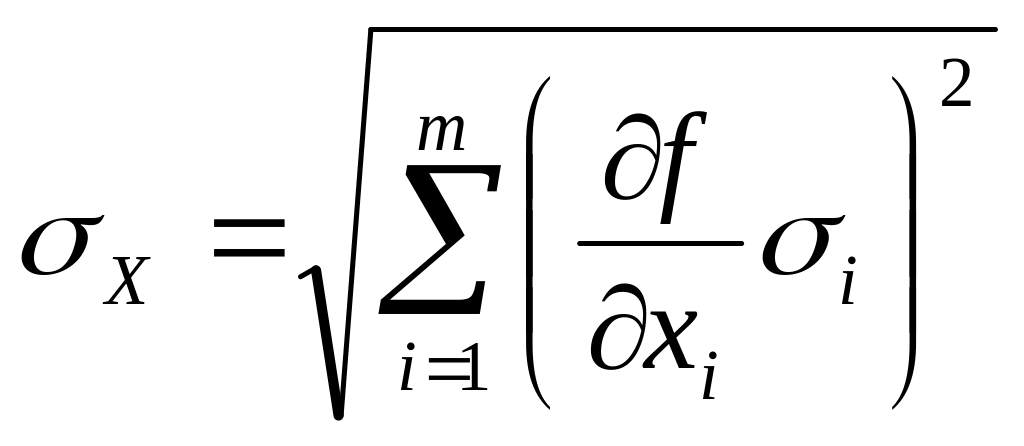, (3.10).

Если случайные погрешности аргументов подчиняются нормальному закону распределения, то их доверительные границы определяются так же, как и при прямых измерениях.