1.5. Требования к содержанию отчёта

Отчёт по лабораторной работе должен содержать: название работы, её цель; чертёж модели с указанием параметров, устанавливаемых в блоках; заполненную таблицу с результатами расчётов; расчётные формулы; графики зависимостей погрешностей от измеряемой величины; класс точности, присвоенный исследуемому «средству измерений»; выводы по работе.

2. Лабораторная работа № 2. Прямые измерения с многократными наблюдениями.

Цель работы. Изучение методики обработки результатов прямых измерений с многократными наблюдениями. Получение точечных и интервальных оценок измеряемой величины и её погрешности. Приобретение навыков использования критериев согласия.

2.1. Теоретическая часть Обработка результатов прямых измерений с многократными наблюдениями

При обработке результатов измерений с многократными наблюдениями, согласно ГОСТ 8.207, в качестве оценки результата принимается среднее арифметическое наблюдений

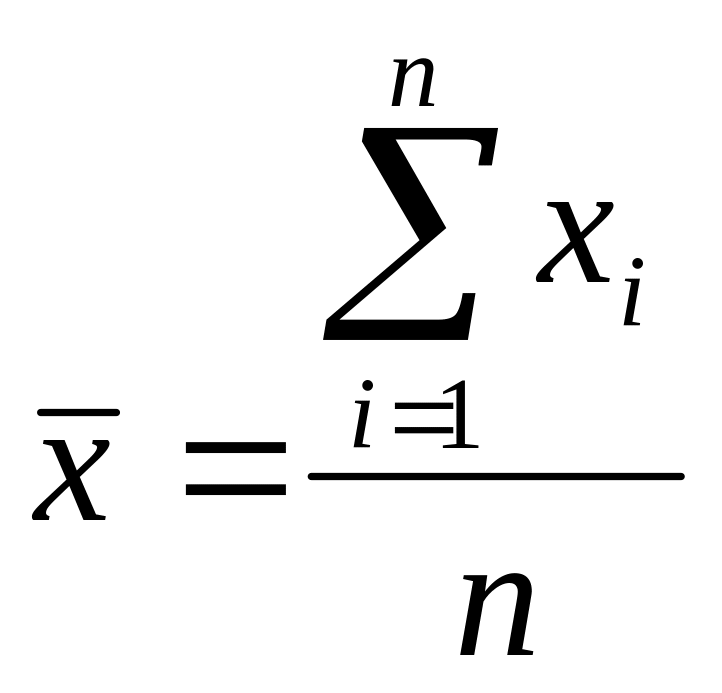, (2.1)

где n – количество наблюдений в серии.

При этом если наблюдения в серии подчиняются нормальному закону, то их среднее подчиняется распределению Стьюдента с n – 1 числом степеней свободы. Мерой рассеяния результата служит СКО среднего арифметического

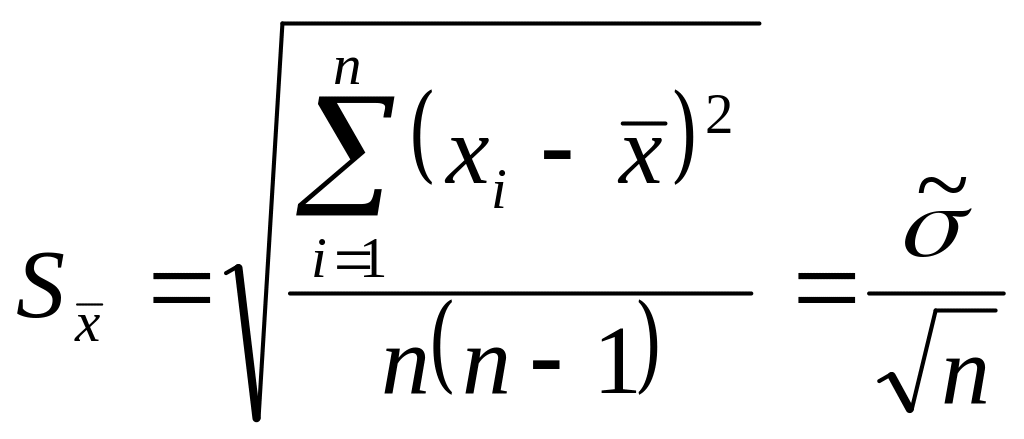, (2.2)

где – оценка СКО наблюдений.

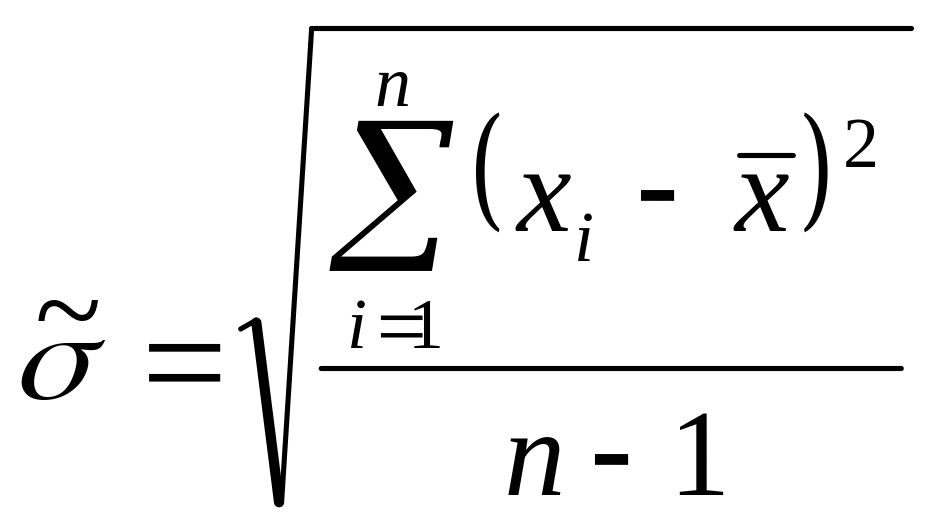. (2.3)

Обработка результатов выполняется в следующей последовательности:

1. Исключаются известные систематические погрешности.

2. Вычисляется среднее арифметическое исправленных наблюдений

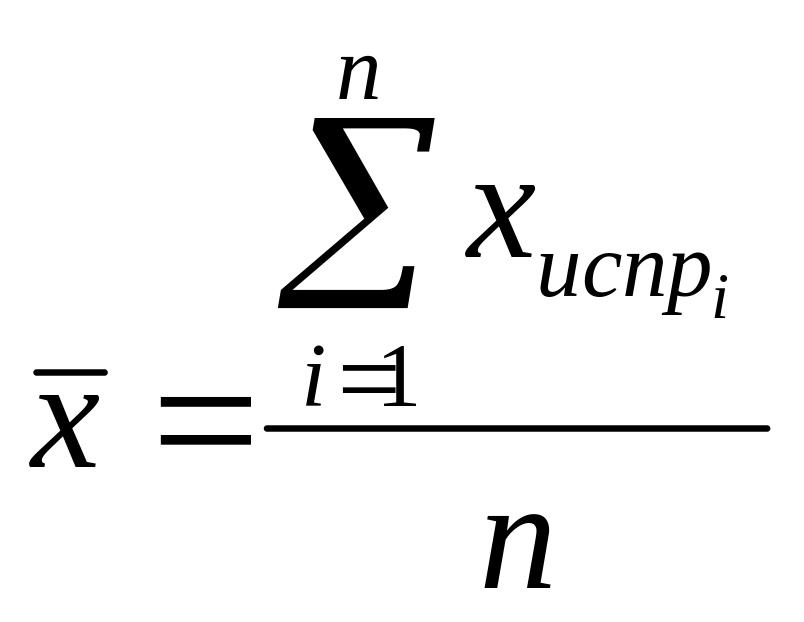. (2.4)

3. Вычисляется оценка СКО наблюдений

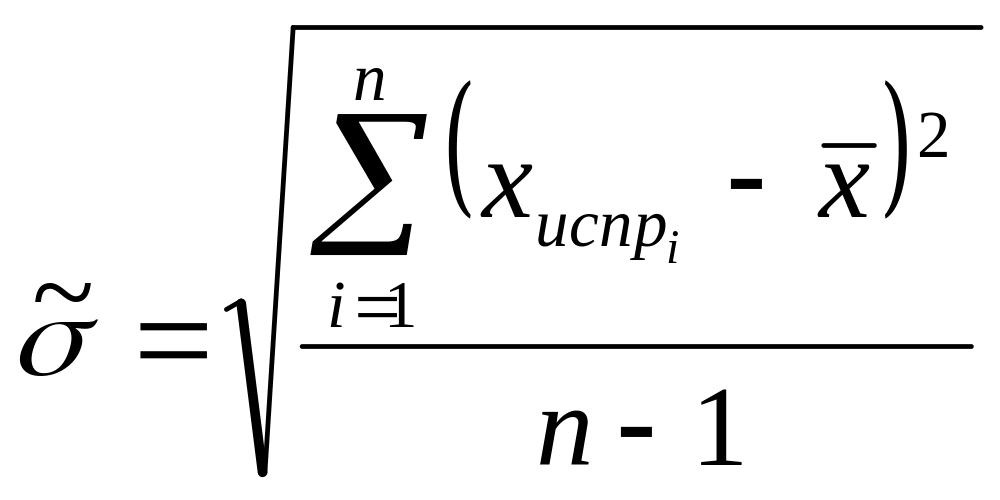. (2.5)

4. Выполняется проверка наблюдений на наличие грубых погрешностей, при необходимости – их исключение и повторное вычисление среднего арифметического и оценки СКО наблюдений (п.п. 2, 3). Критерий, по которому обнаруживаются грубые погрешности, указывается в методике выполнения конкретного измерения. (В качестве примера можно привести критерий «3», согласно которому, если наблюдение не укладывается в интервал [ ; 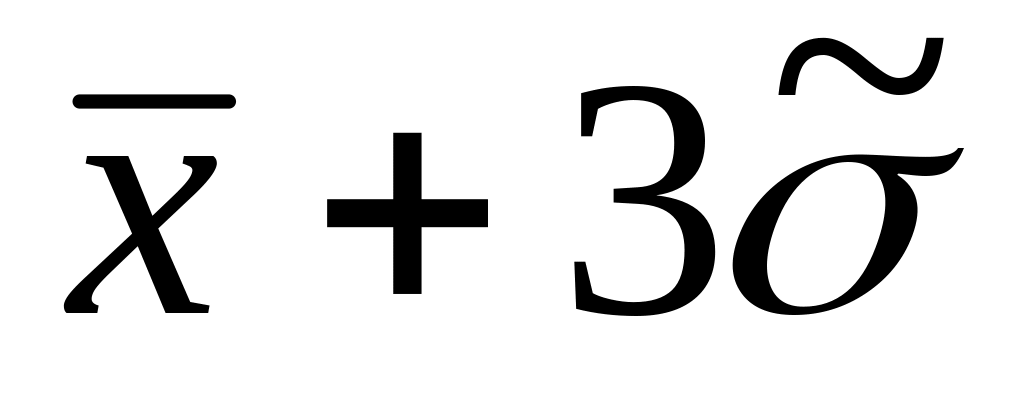], его следует признать ошибочным и отбросить.)

5. Вычисляется оценка СКО результата

. (2.6)

6. Выполняется проверка подчинения результатов наблюдений нормальному закону распределения. При этом если количество наблюдений более 50, рекомендуется применять критерии согласия ² Пирсона или ² Мизеса-Смирнова; если количество наблюдений находится в диапазоне от 15 до 50, предпочтительным является составной критерий; если количество наблюдений не превышает 15, их принадлежность к нормальному закону распределения не проверяется.

7. Вычисляются доверительные границы случайной погрешности результата

, (2.7)

где t_q;n–1 – квантиль распределения Стьюдента с n – 1 числом степеней свободы, соответствующая вероятности q:

; (2.8)

P_д – доверительная вероятность.

8. Вычисляются доверительные границы неисключённой систематической погрешности (НСП) результата

, (2.9)

где _i – доверительная граница i-й составляющей НСП;

m – количество составляющих НСП;

k – коэффициент, определяемый принятой доверительной вероятностью (для P_д = 0,95 k = 1,1).

9. Вычисляются доверительные границы суммарной погрешности результата.

Если

, (2.10)

то НСП пренебрегают, а в качестве доверительных границ погрешности результата  принимают ±.

Если

, (2.11)

то пренебрегают случайной погрешностью и принимают, что граница погрешности результата  = ±.

Если оба неравенства (2.10) и (2.11) не выполняются, при расчёте доверительных границ результата учитывают обе составляющие погрешности:

, (2.12)

где S_ – оценка суммарного СКО результата измерения

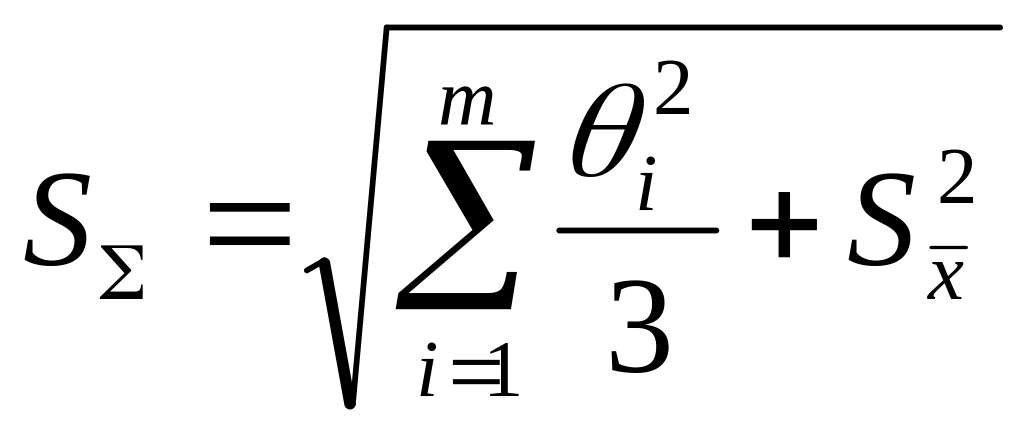; (2.13)

K – коэффициент, вычисляемый по эмпирическому выражению

. (2.14)

Результаты измерений представляют в виде

; P_д. (2.15)

При отсутствии данных о законах распределения погрешностей результата и необходимости дальнейшей обработки или анализа погрешностей, результат представляют в форме

; ; n; . (2.16)