Классы точности средств измерений

Класс точности – обобщённая метрологическая характеристика средства измерений, устанавливающая пределы основных и дополнительных погрешностей.

Согласно ГОСТ 8.401–90, существует четыре способа нормирования основных погрешностей средств измерений, в зависимости от преобладания той или иной погрешности.

1. Для средств измерений с чисто аддитивной погрешностью нормирование выполняется в приведённой форме по выражению

, %, (1.4)

где: X_п – предельная абсолютная погрешность измерения;

X_п – предельная приведённая погрешность измерения;

X_норм – нормирующее значение;

p – положительное число, выбираемое из ряда:

[1; 1,5; (1,6); 2; 2,5; (3); 4; 5; 6]10ⁿ; (1.5)

n = 1; 0; –1; …; –;

(числа, взятые в круглые скобки, не используют для назначения классов точности вновь разрабатываемым средствам измерения).

В качестве нормирующего значения принимают:

1. для шкал, у которых нулевая отметка находится в начале шкалы, или за её пределами – верхний предел измерения;

2. для шкал, у которых нулевая отметка находится между начальным и конечным значениями диапазона измерений – диапазон измерений (сумма по модулю верхнего и нижнего пределов);

3. для шкал с условным нулём (например, температурная шкала Цельсия) – диапазон измерений;

4. для резко неравномерных шкал (например, аналогового омметра) – длину шкалы (угол максимального поворота стрелки прибора).

Класс точности в этом случае обозначается на шкале прибора числом без дополнительных знаков, или, если в качестве нормирующего значения была принята длина шкалы, символом , где вместо X указывается численное значение предельной приведённой погрешности измерения в процентах.

2. Для средств измерения с чисто мультипликативной погрешностью класс точности нормируется в относительной форме по одночленной формуле:

, %, (1.6)

где: X_п – предельная относительная погрешность измерения;

X –значение измеряемой величины;

q – положительное число, выбираемое из ряда (1.5).

Класс точности на шкале прибора в этом случае обозначается числом в окружности, например .

3. Для средств измерений, погрешность которых имеет аддитивную и мультипликативную составляющие, предел основной погрешности нормируется в относительной форме по двучленной формуле:

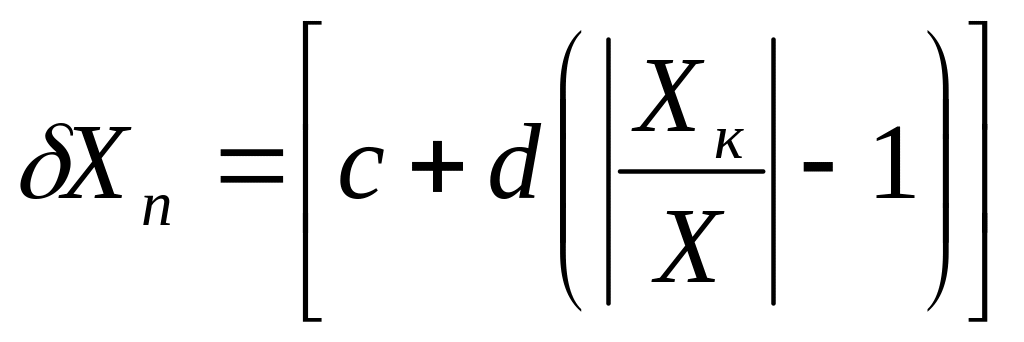, %, (1.7)

где: X_к – конечное значение шкалы (верхний предел измерения);

c, d – положительные числа, выбираемые из ряда (1.5).

Класс точности на шкале или корпусе прибора в этом случае обозначается в виде косой дроби, c / d, (например 0,1 / 0,05).

4. Для некоторых средств измерения (многозначных мер и т. п.) применяется нормирование предельной погрешности в абсолютной форме:

_п. (1.8)

Класс точности при этом обозначается в виде латинской буквы, или римской цифры, причём, чем меньше цифра (или ближе к началу алфавита буква), тем точнее данное средство измерения.

1.2. Порядок выполнения работы.

1. Собрать схему, изображённую на рис. 1.1.

2. В окне настройки блока constant 1 установить значение 0, в окнах блоков constant 2, gaussian и gain – параметры согласно своему варианту (табл. 1.2).

3. Запустить модель в пошаговом режиме (Single Step (F10)). Заданное и полученное значения занести в таблицу (табл. 1.1). (X_ист – значение, введённое в блок constant 1, X_изм – показание блока display.)

4. Повторить п. 3 дважды.

5. Вводя в блок constant 1 следующие значения (согласно своему варианту), повторить п.п. 3, 4. (Для каждого значения, введённого в блок constant 1, должно быть получено по 3 измеренных значения).

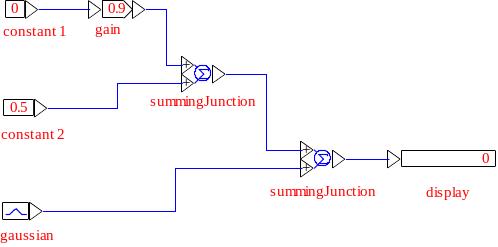
Рис. 1.1

6. Рассчитать абсолютные, относительные и приведённые погрешности результатов измерений, занести их в таблицу.

7. По результатам расчётов построить графики зависимостей абсолютной, относительной и приведённой погрешностей измерения от истинного значения измеряемой величины X = f(X_ист), X = f(X_ист), X = f(X_ист). (Графики должны быть точечного типа без соединения точек линиями).

8. Определить класс точности исследуемого «средства измерения» по приведённой погрешности (в качестве нормирующего значения принять диапазон значений измеряемой величины).

Таблица 1.1

№ опыта	Измерено		Вычислено
	Xист	Xизм	X	X, %	X, %
1
2
					
33