5. Лабораторная работа № 5. Динамический режим работы средств измерений.

Цель работы. Изучение влияния динамических характеристик средств измерений на динамическую погрешность при отсутствии и наличии корректирующего звена.

5.1. Теоретическая часть Динамические погрешности измерений

Динамическим режимом работы средства измерений называют режим, при котором нельзя пренебречь его инерционными свойствами. При этом в общей погрешности результата измерений появляется дополнительная составляющая – динамическая погрешность.

При измерении физической величины, изменяющейся во времени динамическая погрешность в общем виде также будет являться функцией времени:

. (5.1)

Возможно также появление динамической погрешности при изменении постоянной (либо весьма медленно изменяющейся) физической величины средством измерений со значительной инерционностью.

Цель обработки результатов динамических измерений – либо нахождение сигнала на выходе средства измерений по известному сигналу на его входе, либо решение обратной задачи. Для этого необходимо знать динамические характеристики средств измерений.

Различают полные и частные динамические характеристики средств измерений. К полным относят: дифференциальное уравнение; передаточную функцию; переходную и импульсную переходную характеристику; амплитудно- и фазо- и амплитуднофазочастотные характеристики. Частные динамические характеристики являются либо отдельными параметрами полных, либо связаны с ними определёнными функциональными зависимостями (например: постоянная времени, время успокоения и т. п.).

Полные динамические характеристики средств измерений.

1. Дифференциальное уравнение.

Для многих СИ динамический режим может быть описан дифференциальным уравнением вида:

, (5.2)

где A_i, B_i – постоянные коэффициенты.

При x_изм = const и x_ист = const дифференциальное уравнение вырождается в алгебраическое

A₀x_изм = B₀x_ист (5.3)

или

x_изм = Kx_ист, (5.4)

где – номинальный коэффициент преобразования средства измерений.

Несмотря на то, что дифференциальное уравнение позволяет точно определять динамическую погрешность, практическая трудность определения коэффициентов A_i и B_i привела к тому, что дифференциальное уравнение достаточно редко используют в качестве динамической характеристики.

2. Передаточная функция.

Если в дифференциальном уравнении заменить оператор дифференцирования на оператор Лапласа p, то уравнение (5.2) можно записать в операторной форме:

(5.5).

Передаточной функцией W(p) называют отношение изображения по Лапласу выходной величины к изображению входной:

. (5.6)

Часто передаточные функции записывают в виде отношения двух полиномов:

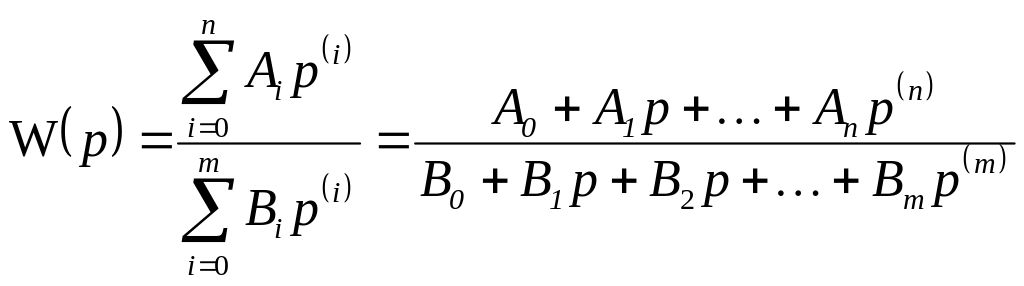. (5.7)

Как правило, передаточные функции такого вида достаточно хорошо характеризуют динамические свойства СИ при n = 2 – 3, причём n < m.

Зная передаточную функцию СИ, можно по известному изображению входного воздействия получить изображение воздействия на выходе СИ, либо решить обратную задачу.

3. Частотные характеристики.

Если в передаточной функции заменить оператор p на j, то получится комплексная амплитуднофазочастотная характеристика (АФЧХ):

, (5.8)

модуль которой A() является амплитудночастотной характеристикой (АЧХ), а аргумент () – фазочастотной характеристикой (ФЧХ).

4. Переходная и импульсная переходная характеристики.

Переходной характеристикой h(t) средства измерений называют его отклик на ступенчатое возмущение единичной высоты 1(t) (единичная функция или функция Хевисайда). Производная от единичной функции называется дельта-функцией Дирака и представляет собой импульс бесконечно малой ширины и бесконечно большой амплитуды. Реакция средства измерений при подаче на его вход дельта-функции называется импульсной (или весовой) переходной характеристикой g(t).

Переходную и импульсную переходную характеристики средства измерений достаточно легко получить, подав на его вход ступенчатый или импульсный сигнал и зарегистрировав его отклик.

Полные динамические характеристики линейных аналоговых звеньев связаны между собой соотношениями:

; (5.9)

; (5.10)

; (5.11)

; (5.12)

. (5.13)