
- •Билет №1. Доказать теорему Ролля.
- •Доказать теорему о предельном переходе в неравенстве.
- •Вывести уравнение наклонной асимптоты.
- •Билет №6. Доказать необходимое условие возрастания дифференцируемой функции.
- •Предел числовой последовательности. Сформулировать признак сходимости монотонной последовательности. Доказать теорему о единственности предела.
- •Билет №7. Доказать необходимое условие экстремума дифференцируемой функции.
- •Вывести 1 замечательный предел:
- •Билет №8-1. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
- •Билет №8-2. Векторная функция скалярного аргумента: и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.
- •Билет №9-1. Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
- •Билет №9-2.
- •Доказать теорему о пределе произведения функций.
- •Билет №16-2.
- •Доказать теорему о связи функции, её предела и бесконечно малой.
- •Билет №22.
- •Вывести уравнение касательной и нормали к плоской кривой.
- •Билет №24. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
- •Вывести формулу для производной частного от деления двух функций.
- •Билет №25. Доказать первое достаточное условие экстремума функции.
- •Сформулировать определение функции, непрерывной на отрезке. Свойства функций, непрерывных на отрезке.
- •Билет №26. Доказать теоремы Ролля и Ферма.
- •Вывести формулу для производной обратной функции.
- •Билет №27. Необходимое и достаточное условие существования точки перегиба графика функции. Доказать достаточное условие. Первое достаточное условие существования точки перегиба.
- •Второе достаточное условие существования точки перегиба.
- •Определение б.Б. Функций. Теорема об их связи с б.М. Функциями.
Билет №1. Доказать теорему Ролля.
Пусть дана функция
![]() .
.
Определена и непрерывна на отрезке
 .
.Дифференцируема на интервале
 .
.И на концах отрезка принимает одинаковые значения.
 .
.
Тогда найдется, по крайней мере, 1
![]()
![]() ,
принадлежащая интервалу
,
принадлежащая интервалу![]() .
.
Доказательство: Т.к. функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то согласно 2 теореме Вейерштрасса она
достигает своего минимального и
максимального значения.
,
то согласно 2 теореме Вейерштрасса она
достигает своего минимального и
максимального значения.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Случаи:
 ,
, - любое из интервала
- любое из интервала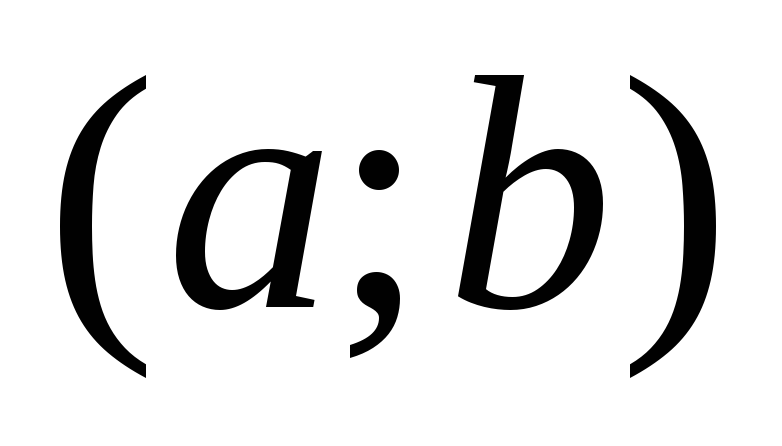
 в силу 3-го условия теоремы, одно из
значений минимального или максимального
достигается функцией во внутренней
точке интервала
в силу 3-го условия теоремы, одно из
значений минимального или максимального
достигается функцией во внутренней
точке интервала .
.
Согласно второму условию теоремы Ролля,
функция дифференцируема на интервале
![]() в любой точке, то по теореме Ферма
существует
в любой точке, то по теореме Ферма
существует![]() .
.
Доказать теорему о предельном переходе в неравенстве.
Пусть
![]() при
при![]() имеет конечный предел А1,
имеет конечный предел А1,![]() при
при![]() имеет конечный предел А2, и
существует
имеет конечный предел А2, и
существует![]() :
:![]() для
для![]() ,
тогда
,
тогда![]() .
.
Доказательство:
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
Пусть
![]()
Это неравенство выполняется для любого
![]() ,
,![]() отсюда
отсюда![]()
Билет №2.
Доказать теорему Лагранжа.
Пусть функция
![]() .
.
Определена и непрерывна на отрезке
 .
.Дифференцируема на интервале
 .
.
Тогда существует
![]() из интервала
из интервала![]() .
.
Доказательство: Рассмотрим вспомогательную
функцию
![]() ,
где
,
где![]() - константа.
- константа.

Она непрерывна на

дифференцируема на
 .
.
Все условия теоремы Ролля выполняются
![]() существует
существует![]() из
из![]()
![]()
Формула Маклорена
для
![]() с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
![]() ,
где
,
где
1)![]() Пеано
Пеано
2) ![]() где
где ![]() - Лагранж
- Лагранж
3) ![]() - Коши
- Коши
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
т.к.sinx-
нечет., то вып. усл.:
,
т.к.sinx-
нечет., то вып. усл.:![]()
Билет №3.
Формула Маклорена
для
![]() с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
![]() ,
где
,
где
1)![]() Пеано
Пеано
2) ![]() где
где ![]() - Лагранж
- Лагранж
3) ![]() - Коши
- Коши
![]() ,
,![]() ,
,![]() ;
;![]()
Сравнение на бесконечности роста показательной, степенной и логарифмических функций.
1)![]()
![]() ,
гдеs>0,x>0;
,
гдеs>0,x>0;![]() .
.![]()
2)
![]() ;
;![]() ;
; =
=![]() ;
; .
.
3)
![]() (по транзитивности)
(по транзитивности)![]()
Билет №4.
Доказать первое достаточное условие экстремума функции.
Пусть функция
![]() определена и дифференцируема в окрестности
точки С. Для того, чтобы точка С являлась
точкой локального экстремума, достаточно
чтобы при переходе значений аргумента
через точку С производная функции меняла
знак с “+” на “-” – локальный максимум,
с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности
точки С. Для того, чтобы точка С являлась
точкой локального экстремума, достаточно
чтобы при переходе значений аргумента
через точку С производная функции меняла
знак с “+” на “-” – локальный максимум,
с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку Xиз указанной окрестности, тогда:
на
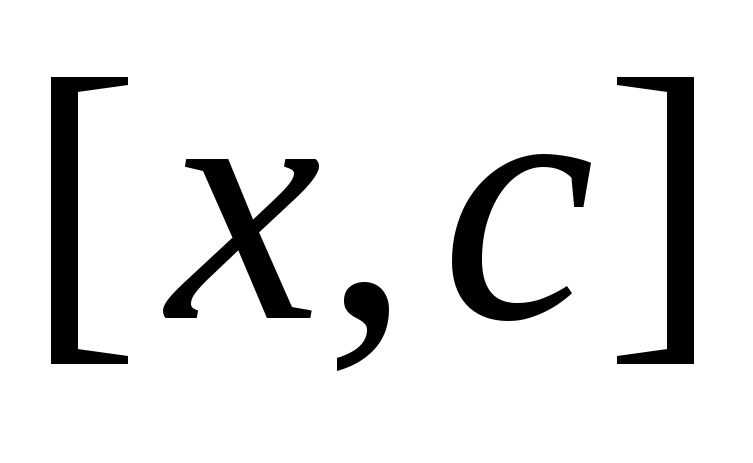
 - непрерывна.
- непрерывна.на
 - дифференцируема.
- дифференцируема.
По т. Лагранжа
![]() ,
где
,
где![]() ,
т.к.
,
т.к.![]() ,
то
,
то![]()
на
![]() :
:![]() где
где![]() ,
,![]()
Доказать теорему о связи функции, её предела и бесконечно малой.
Для того, чтобы функция
![]() ,
определённая в
,
определённая в![]() имела конечный предел при
имела конечный предел при![]() ,
необходимо и достаточно чтобы эту
функцию можно было представить в виде
суммы предела и б.м.ф. при
,
необходимо и достаточно чтобы эту
функцию можно было представить в виде
суммы предела и б.м.ф. при![]() (
(![]() ,
где
,
где![]() - б.м.ф. при
- б.м.ф. при![]() ).
).
Доказательство: IНеобходимость:
Дано:
![]()
Доказать:
![]() ,
где
,
где![]() - б.м.ф. при
- б.м.ф. при![]() .
.
![]()
Пусть
![]() по определению б.м.ф
по определению б.м.ф![]() - б.м.ф. при
- б.м.ф. при![]() .
.
![]()
IIДостаточность:
Дано:
![]() ,
где
,
где![]() - б.м.ф. при
- б.м.ф. при![]() .
.
Доказать:
![]()
![]()
Билет №5.
Доказать второе достаточное условие экстремума.
Пусть функция
![]() определена и имеет в окрестности точки
с производную доn-го
порядка включительно, причем в самой
точке с все производные до (n-1)-го
порядка включительно равны 0, аn-ая
производная в точке С отлична от нуля.
Еслиn– четное, тогда С
– точка локального экстремума, в
частности, если
определена и имеет в окрестности точки
с производную доn-го
порядка включительно, причем в самой
точке с все производные до (n-1)-го
порядка включительно равны 0, аn-ая
производная в точке С отлична от нуля.
Еслиn– четное, тогда С
– точка локального экстремума, в
частности, если![]() ,
тоx=c–
локальный минимум, если
,
тоx=c–
локальный минимум, если![]() ,
тоx=c–
локальный максимум.
,
тоx=c–
локальный максимум.
Доказательство: Запишем формулу Тейлора с остаточным членом в форме Пеано с центром в точке С.
 ,
где
,
где![]() -
б.м.ф. при
-
б.м.ф. при![]() .
Пустьn– четное, тогда
.
Пустьn– четное, тогда![]() не меняет знак при переходе через С.
не меняет знак при переходе через С.![]()
![]() в которой функция сохраняет знак своего
предела.
в которой функция сохраняет знак своего
предела.![]() ,
,![]() .
.![]() .
.![]() ,
если
,
если![]() -
точка локального экстремума.
-
точка локального экстремума.
