
- •Зміст дисципліни за темами
- •Тема 1. Концептуальні аспекти економетричного моделювання економіки
- •Тема 2. Принципи побудови економетричних моделей. Парна та множинна лінійна регресія
- •Економетрика
- •2. Об'єкт, предмет, мета і завдання економетрії
- •3. Основні етапи економетричного аналізу
- •4. Економічні задачі, які розв'язують за допомогою економетричних методів
- •5. Основні етапи зародження та розвитку економетрії
- •Тема: Регресійні моделі
- •1. Поняття регресії
- •3. Парна лінійна регресія
- •4. Теоретична і розрахункова моделі
- •5. Метод найменших квадратів – метод розрахунку параметрів моделі.
- •6. Дисперсійний аналіз моделі
- •Тема: Загальна лінійна економетрична модель
- •1. Множинна лінійна регресія
- •2. Передумови застосування метода найменших квадратів
- •3. Дисперсійний і регресійний аналіз моделей
- •4. Точковий та інтервальльний прогноз
- •5. Перевірка якості та статистичної значущості моделі
- •1. Постановка задачі.
- •4. Розрахункова таблиця:
- •5. Графік моделі у „хмарі” розсіювання
- •6. Дисперсійний аналіз лінійної моделі:
- •7. Значущість оцінок параметрів і моделі:
- •8. Прогноз:
- •9. Аналіз лінійної моделі:
- •Завдання №1 на самостійну роботу
- •1). Побудувати економетричну модель залежності між факторами за допомогою функції «линейн»:
- •Тема: Нелінійні моделі
- •2. Нелінійні регресії 1-го класу
- •2.1. Поліноміальна модель
- •2.2. Гіперболічна модель
- •3. Нелінійні регресії 2-го класу
- •3.1. Показникова моделі
- •3.2. Степенева модель
- •4. Виробнича функція Кобба – Дугласа
- •Завдання №2 на самостійну роботу
- •Тема: Фіктивні змінні в регресійних моделях
- •1. Необхідність використання фіктивних змінних
- •2. Моделі ancova
- •2.1. Ancova - Модель при наявності у фіктивної змінної двох альтернатив
- •2.2. Моделі ancova за наявності у якісних змінних більш двох альтернатив
- •3. Використання фіктивних змінних у сезонному аналізі
- •Завдання № 3* на самостійну роботу Розрахувати моделі із фіктивними змінними :
- •Дослідити розраховану модель на значущість. Тема: Мультиколінеарність факторів моделі
- •Поняття мультиколінеарності
- •Основні наслідки мультиколінеарності:
- •Дослідження наявності мультиколінеарності
- •Ознаки мультиколінеарності
- •Завдання №4 на самостійну роботу
- •Тема: Гетероскедастичність моделі
- •1. Поняття гетероскедастнчності та її наслідки
- •2. Перевірка гетероскедастичності
- •Тема: Автокореляція відхилень (залишків)
- •1. Поняття автокореляції та її наслідки
- •Перевірка наявності автокореляції
- •Завдання № 5 на самостійну роботу
4. Точковий та інтервальльний прогноз
1. Точковий прогноз Х*пр = (1, х*1, х*2 ,..., х*n) , Y*пр = Х*пр· Â.
2. Дисперсія прогнозу D пр = Х*пр · Var  ·( Х*пр )т.
3. Дисперсія інтервального прогнозу DІ = De + D пр , σ І =√ DІ.
4. Інтервальний прогноз Y*пр - tα; ( n-m ) · σ І < Y*пр < Y*пр + tα;( n-m ) ·σ І .
5. Перевірка якості та статистичної значущості моделі
1. Статистична значущість коефіцієнтів множинної регресії з т факторами перевіряється на основі t-статистики з (n – m - 1) ступенями свободи, де
n – кількість спостережень, m – кількість факторів моделі, α – поріг значущості моделі :
t фj = | â1| / σâ1
якщо t фj > tα/2; ( n – m -1 ) , знайденого за таблицею розподілу Стьюдента, то маємо статистично значущий коефіцієнт множинної регресії â1;
якщо t фj < ttα/2; ( n – m -1 ), то коефіцієнт множинної регресії â1 є статистично незначущим, а фактор xj не має серйозного впливу на Y, лінійно з Y не пов’язаний.
2. Перевірка загальної якості моделі за коефіцієнтом детермінації R2 = 1- =
знаходиться для перевірки якості рівняння регресії і визначає характер лінійного впливу зміни значень факторів моделі на змінну Y , тобто на скільки відсотків рівняння регресії пояснює поведінку залежної змінної Y.
оцінка статистичної значущості коефіцієнта детермінації R2 проводиться за критерієм Фішера ( F –статистика):
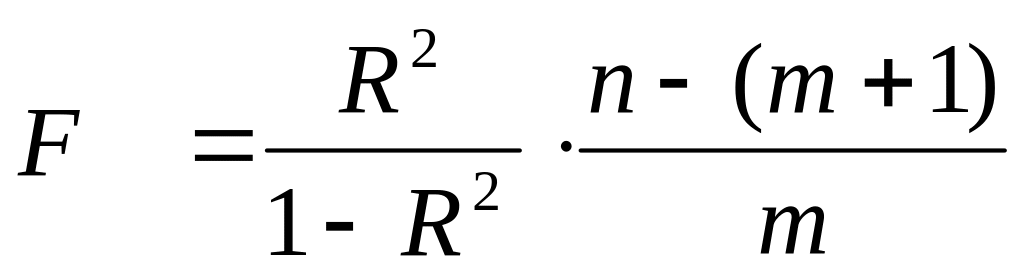 ,
,
F kp = F α; m; n -( m+1 ) , де n – кількість спостережень,
m – кількість факторів моделі, α – поріг значущості моделі.
Якщо F > Fкр, то коефіцієнт R2 є статистично значущим, в протилежному випадку не є статистично значущим.
6. Функція «ЛИНЕЙН» для розрахунку і аналізу багатофакторної лінійної моделі
для отримання результату спочатку треба виділити масив «5 × (m+1)», де m – кількість факторів моделі,
знайти: fх → «Статистические» → «ЛИНЕЙН» і виділити:
- масив Y;
- массив Х;
- константа – «истина» («1»);
- константа – «истина» («1»);
після введення даних натиснути комбінацію клавіш F2 + Ctrl + Shif t+ Enter одночасно.
-
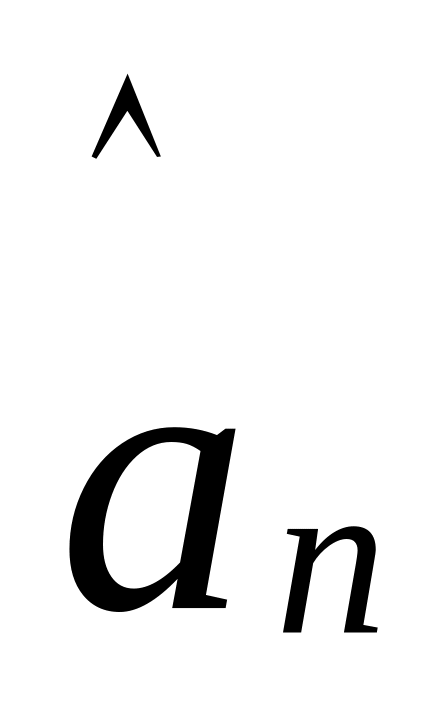
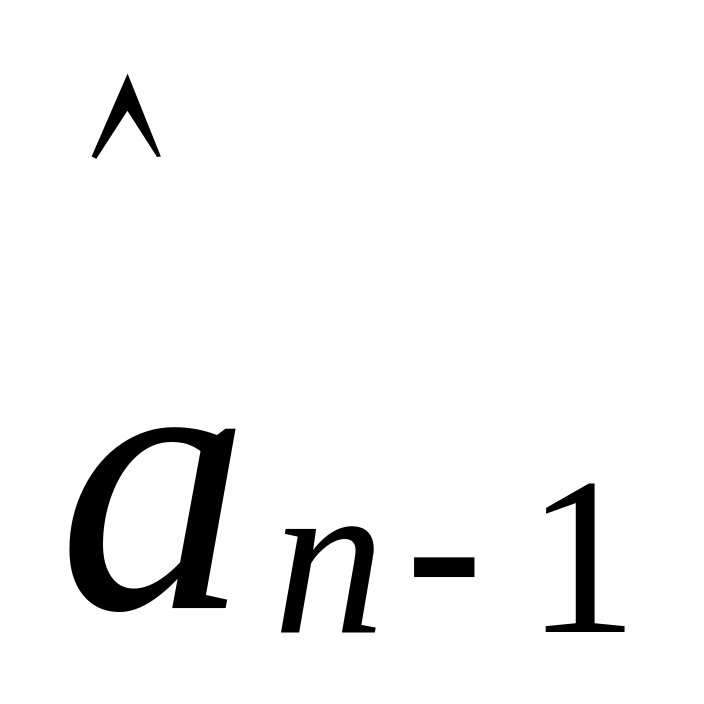
…
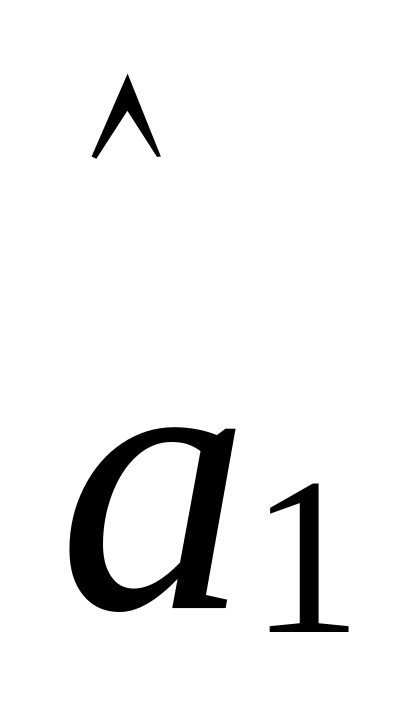
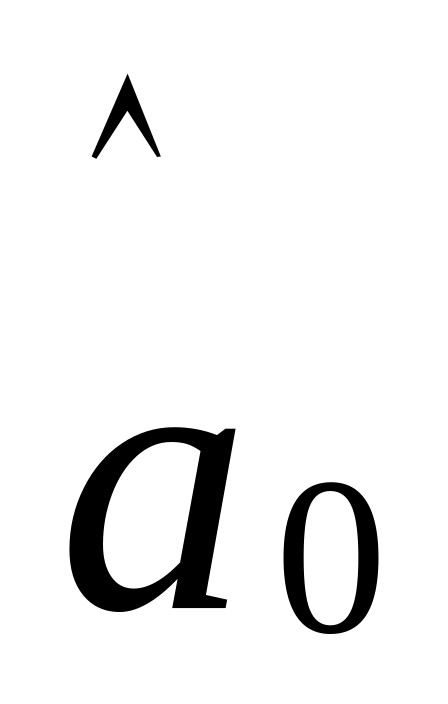

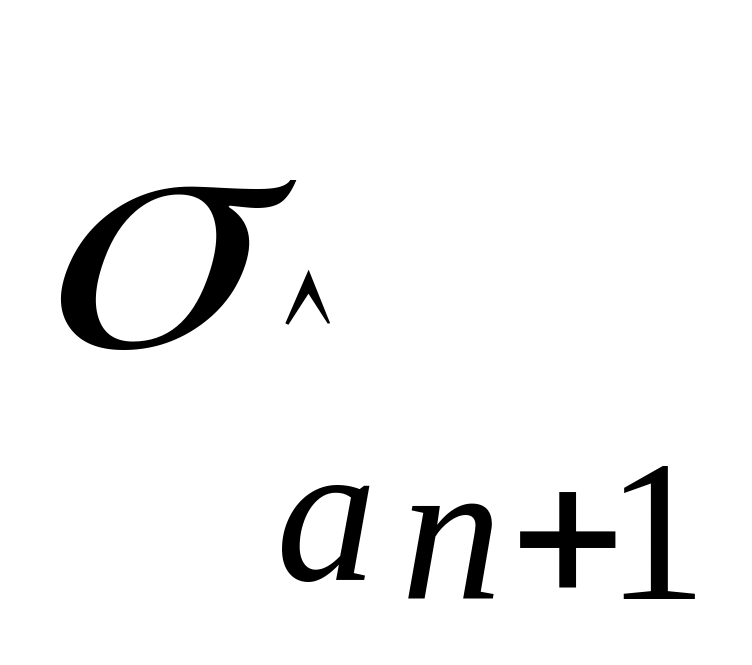
…

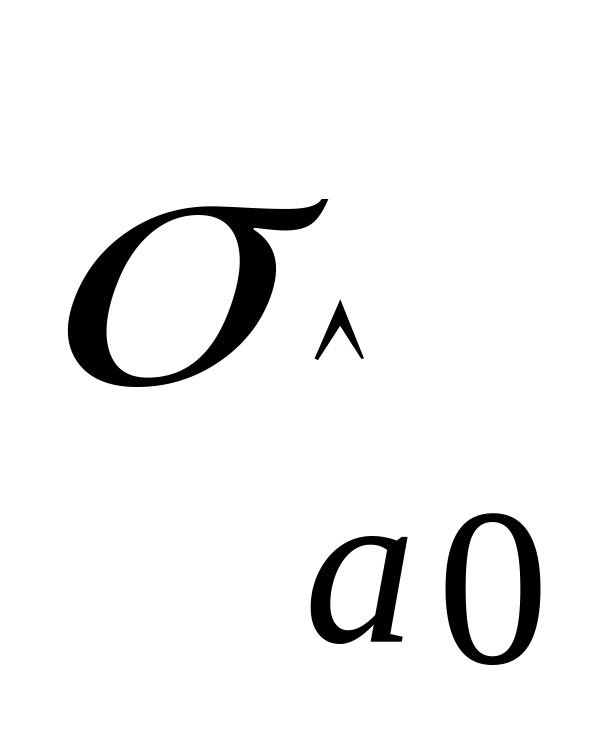
R2
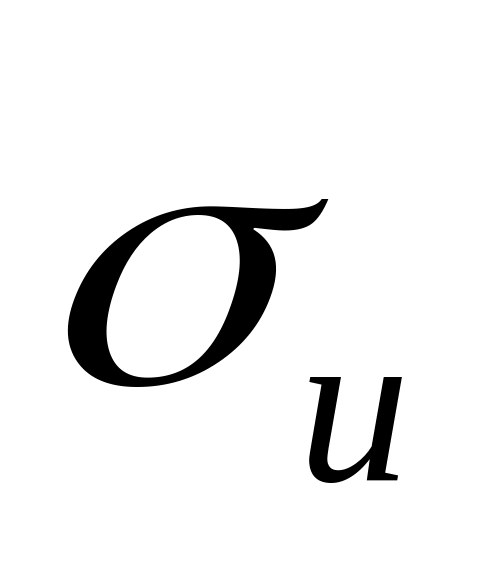
#
#
#
F
Df = n – m -1
#
#
#
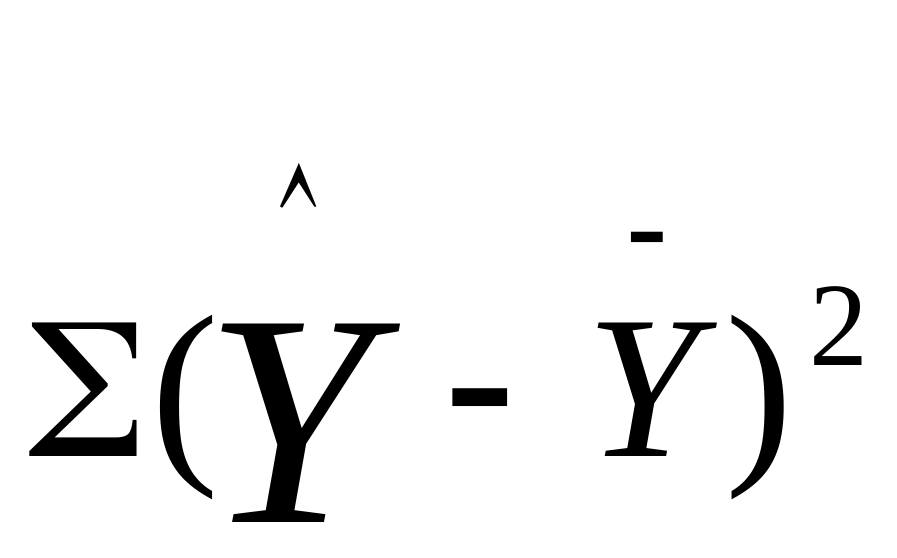
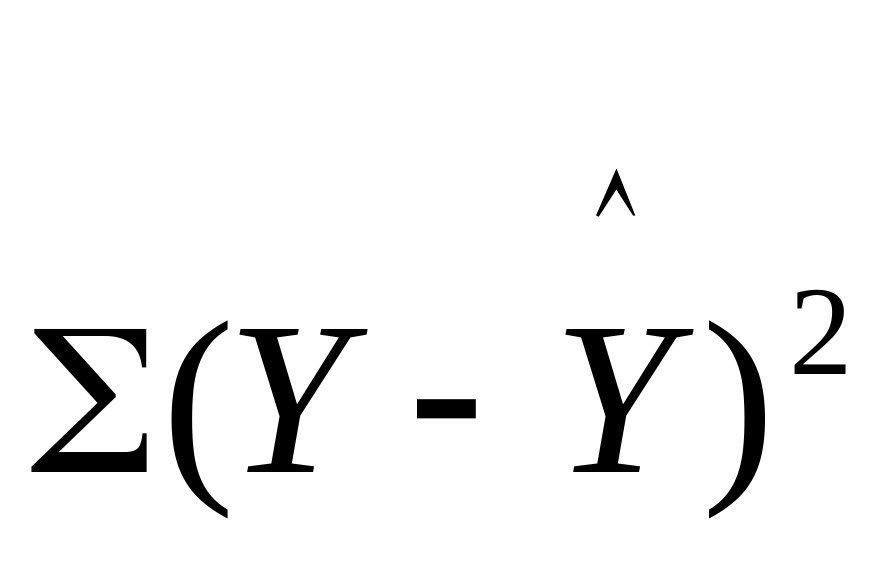
#…
#
#
Розрахункова робота «Економетрична модель парної регресії»
