4. Теоретична і розрахункова моделі

Теоретична лінійна модель Y = a₀ + a_1·x + u, розрахункова модель Y_р= â₀+â_1·x+ û,

де â₀ , â_1, u – відповідні оцінки, наближені значення параметрів теоретичної моделі

â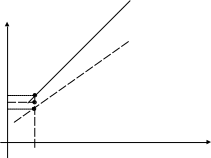 ₀  a_0, â_1· a_1, u  û

у Y_т

Y_р

Y_і(т)

Y_і u

Ŷ_{і (р)} û

x_і х

В цьому рівнянні коефіцієнт a₁ – це частинний коефіцієнт регресії, який характеризує чутливість величини у до зміни фактора х – вплив змінної x на умовне математичне сподівання як зміниться величина фактора Y за умов збільшення фактора Х на одну одиницю.

5. Метод найменших квадратів – метод розрахунку параметрів моделі.

Метод найменших квадратів – метод розрахунку параметрів моделі Y_р= â₀ + â_1·x + û.

Ідея методу базується на тому, що величина е_і має буде мінімальною:

= ∑(y_i - ỳ) або ∑(y_i - ỳ)² або ∑│y_i - ỳ│ min.

Краще всього в ролі функції оцінки відхилень взяти суму квадратів відхилень кожної точки від свого розрахункового значення Q (â₀ , â₁) = = ∑(y_i - ỳ)² = ∑( y_i – (â₀ + â_1·x_і+ û_і))².

Ця функція має min значення в тих точках, де частинні похідні по змінних â₀ , â₁l дорівнюватимуть нулю:

=0, ( y_i – (â₀ + â_1·x_і))(-1) = 0, ∑ y_і – ∑â₀ – ∑ â_1·x_і = 0,

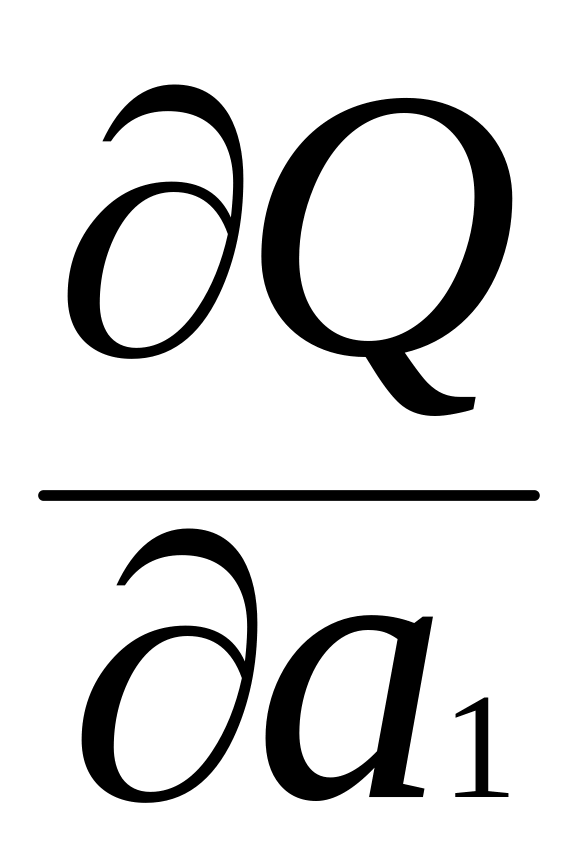=0 (( y_i – (â₀+ â_1·x_і))(- x_i)=0 ∑ y_і·х_і – â₀ ∑ х_і – â₁ ∑ _·x_і² =0,

З аписується остаточна система рівнянь: n â₀ + â₁ ∑ _·x_і = ∑ y_і ,

â₀ ∑ х_і + â₁ ∑ _·x_і² =∑ y_і·х_і ,

n – кількість спостережень.

Розв’язання системи рівнянь проводиться за допомогою оберненої матриці або за правилом Крамера. Основний визначник системи , тому існує єдиний розв'язок системи: . З цього випливає, що лінія регресії проходить через точку, координати якої с середніми значеннями показника Y та фактора X.

ả_{1 = = = .}

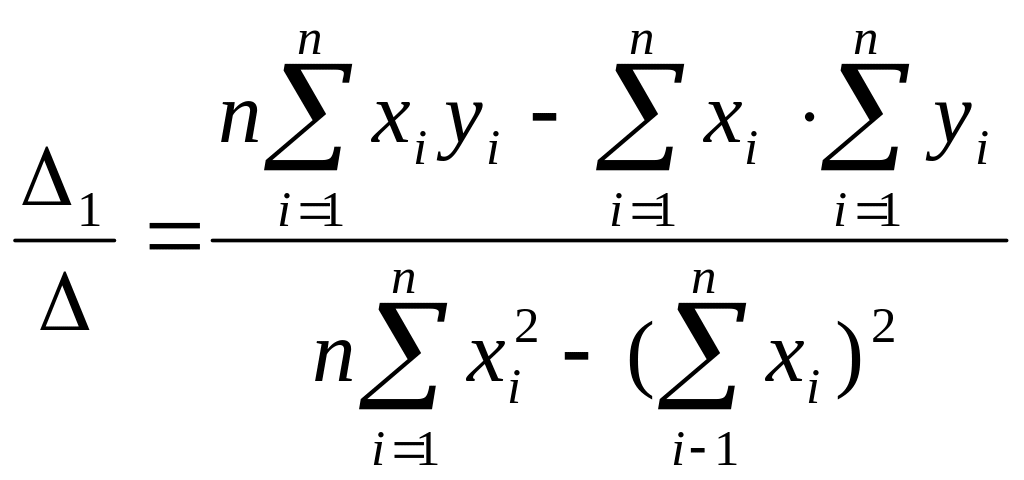Ця рівність означає, що коефіцієнт ả₁ моделі ПЛР дорівнює відношенню кореляційного моменту до дисперсії фактора Х і дорівнює тангенсу кута між лінією регресії і віссю ОХ.

ả_{0 = = = .}

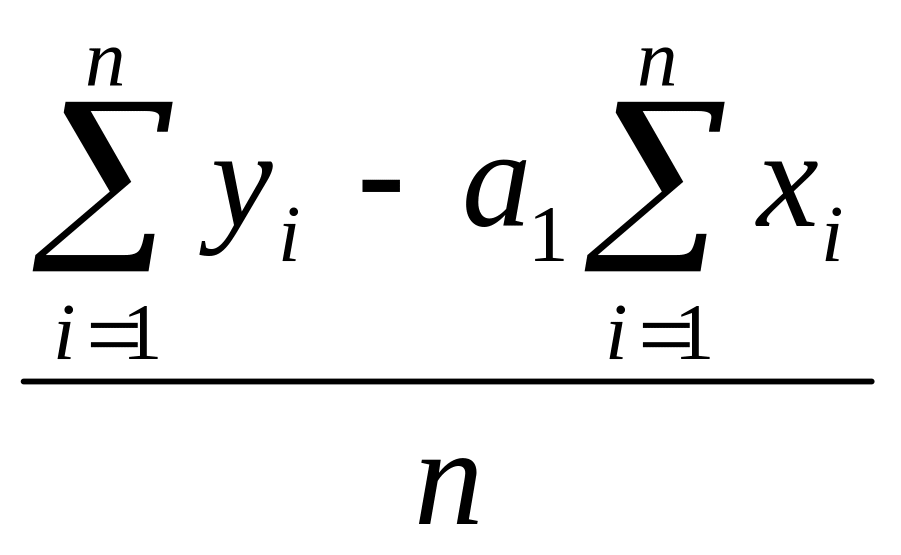Середнє значення прогнозу показника Y _р при значенні фактора Х_р визначається за формулою = ả₀ + ả₁

6. Дисперсійний аналіз моделі

• Дисперсія залишків D_и = 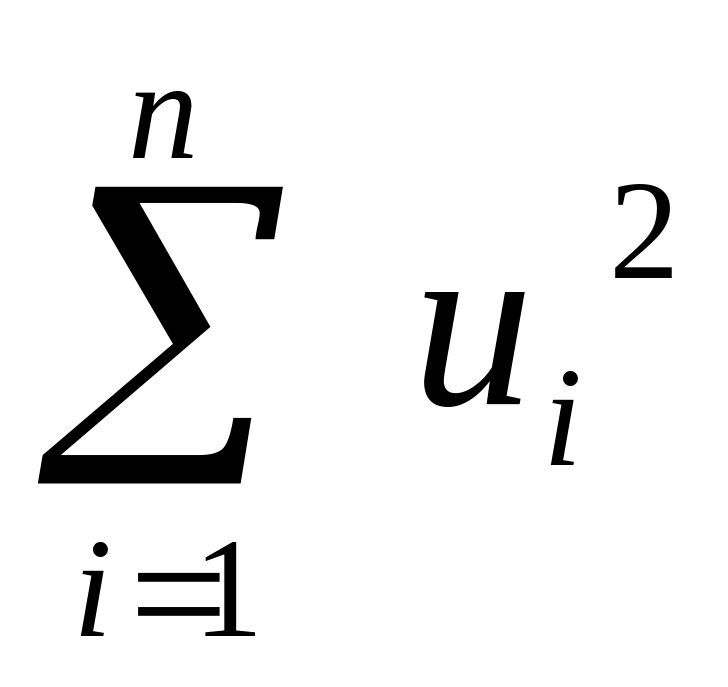= 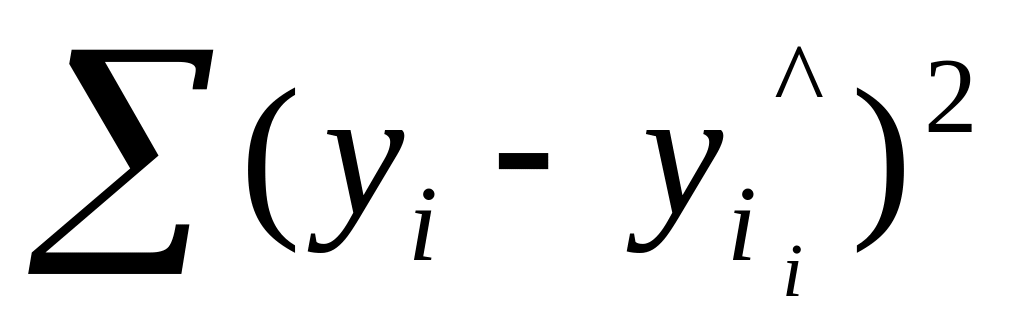характеризує міру відхилень значень залежного фактора y_i від розрахованих значень за моделлю y_i^.

• Дисперсія змінної D_у = 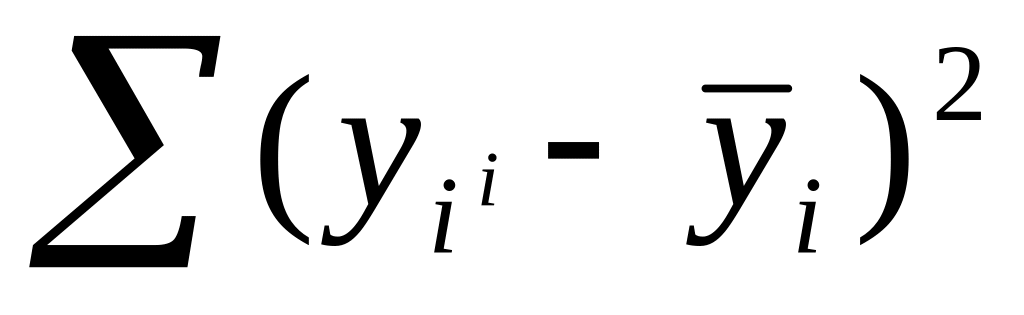характеризує міру відхилень значень залежного фактора y_i від середнього значення

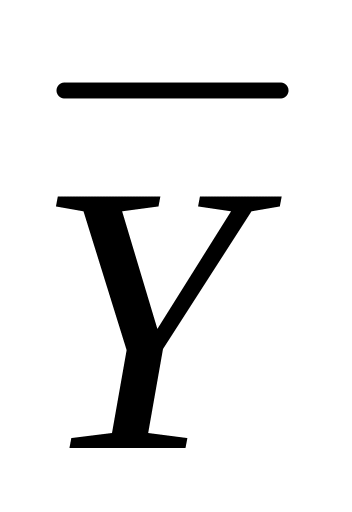
• Коефіцієнт детермінації R² = 1- 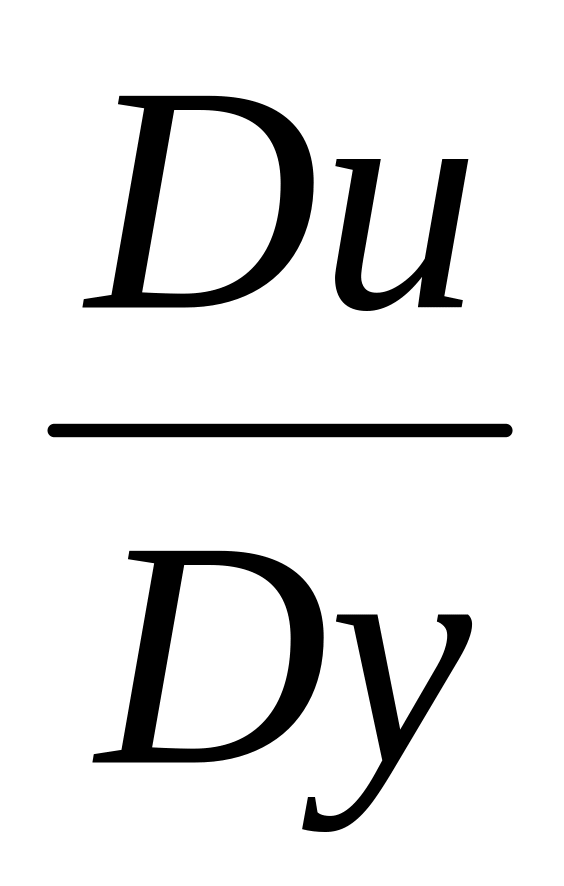= 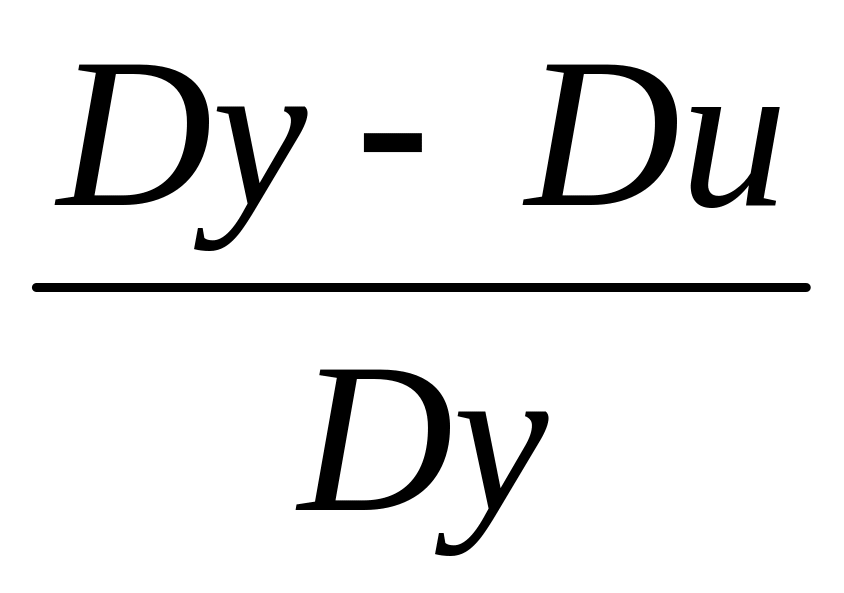є (0;1)

знаходиться для перевірки якості рівняння регресії і визначає характер лінійного впливу зміни значень факторів моделі на змінну Y, тобто на скільки відсотків рівняння регресії пояснює поведінку залежної змінної Y.

Крім того, показник R² може виявитися в ході розрахунків відємним, чому може сприяти: неякісна лінійна модель (звязок в моделі є нелінійним); коефіцієнт моделі а₀ є дуже і дуже малим; малий обсяг статистичних даних.

• Коефіцієнт кореляції R =√ R² характеризує тісноту лінійного зв’язку :

чим тіснішим є лінійний звязок між Х і Y, тим ближче R 1,

чим слабшим є лінійний звязок між Х і Y ,тим ближче R 0.

Крім того, якщо R > 0, то характер зміни Х і Y однаковий ,

якщо R < 0, то характер зміни Х і Y протилежний, (R > 0 при а₁ > 0; R < 0 при а₁ < 0).

якщо r(X,Y) = 0, то величини X та Y некорельовані.

або використовують вибірковий коефіцієнт кореляції R(X,Y ) є (-1;1)

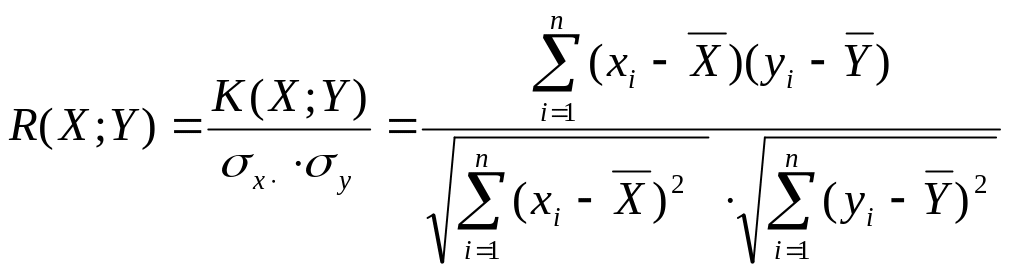
• Стандартне (середнє квадратичне) відхилення оцінки ả₀ : _ả0 = _и

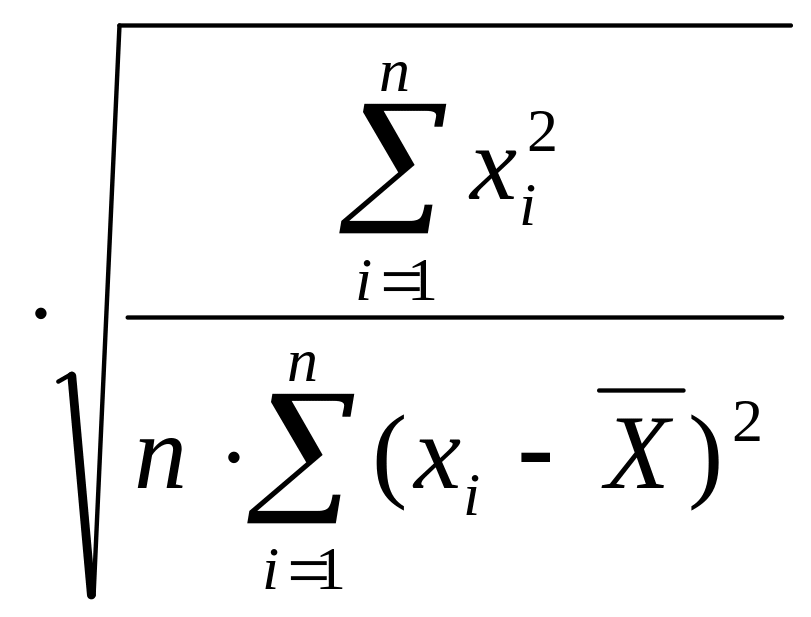
• Стандартне (середнє квадратичне) відхилення вільного члена рівняння регресії оцінки ả₁ знаходять за формулою _ả1 = _и

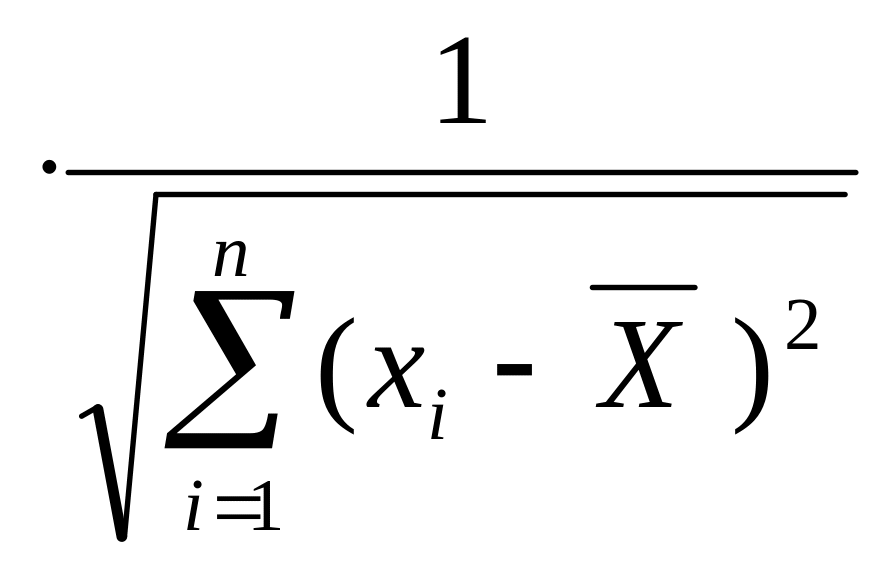
• Інтервали надійності для оцінок :

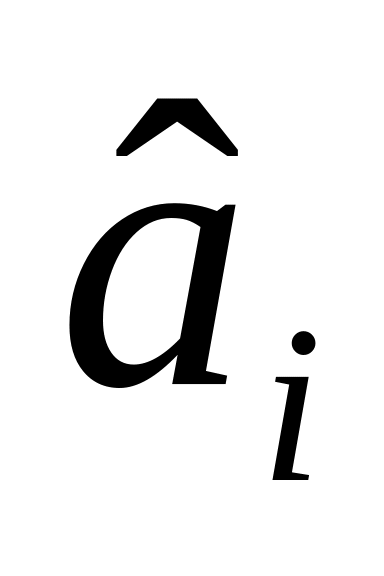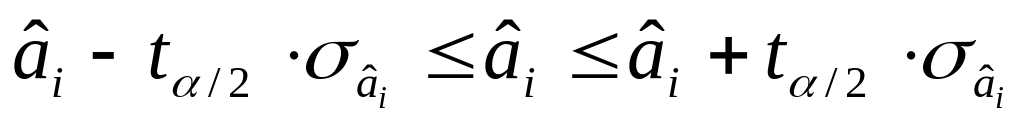
• Межі (інтервали) надійності індивідуальних прогнозних

Y^*_пр - t_{(α/2; ( n-2 ))} · σ _и < Y^*_пр < Y^*_пр + t _{(α/2 ( n -2))} · σ _и

де t_a - статистика Ст'юдента, α- рівень значущості, k = n - 2 ступені свободи.