Московский Государственный Университет им. М.В, Ломоносова

Основы геотехники в криолитозоне.

Часть V. Задачи теплового и механического взаимодействие инженерных сооружений с мерзлыми и оттаивающими грунтами.

(Курс лекций для магистрантов 1-го года обучения)

Москва, 2011.

Тепловое взаимодействие.

Задача 1. Расчет температуры ВМГ у подошвы слоя с годовыми теплооборотами.

Постановка задачи. Рассматривается задача формирования температуры ВМГ у подошвы слоя с годовыми теплооборотами.

Предполагается, что теплообмен между глубинными и поверхностными слоями грунта существует только в период времени от окончания сезонного промерзания грунта до начала его сезонного оттаивания. В остальное время года он практически отсутствует из-за наличия фазовой границы, на которой поддерживается постоянная температура. Поэтому искомая температура определяется суммой градусочасов поверхности грунта только за часть зимнего периода. Эта сумма градусочасов называется импульсом охлаждения. Расчетная схема задачи показана на рис. 5.1.

Рис. 5.1 Схема к расчету температуры ВМГ.

1 – изменение температуры поверхности грунта в течение года; 2 – ход сезонного оттаивания грунта; 3 – ход сезонного промерзания грунта.

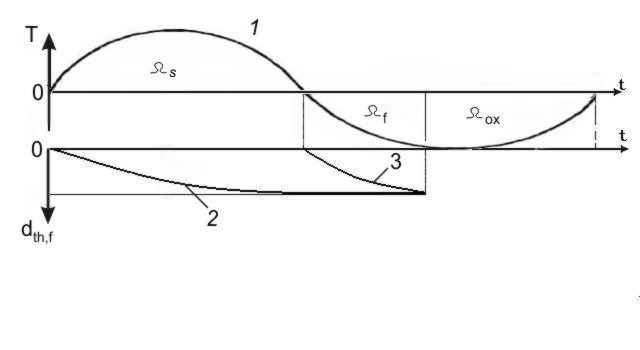
Теоретические основы метода решения задачи. Согласно И.В.Шейнину (Порхаев, 1970) искомая температура равна охлаждающему импульсу деленному на период сезонного колебания наружной температуре воздуха t_y (8760 час):

(5.1)

В свою очередь находится как разность (см. рис. 5.1):

(5.2)

где – сумма градусочасов на дневной поверхности грунта в период охлаждения ВМГ, ⁰С∙ч; - сумма градусочасов на дневной поверхности грунта в зимний период, принимается равным сумме зимних градусочасов атмосферного воздуха, ⁰С∙ч; - сумма градусочасов на дневной поверхности грунта в период промораживания слоя сезонного оттаивания, ⁰С∙ч.

находим из условия равенства слоя сезонного оттаивания слою сезонного промерзания:

, (5.3)

находим по формуле Стефана. Последняя при наличии на дневной поверхности снега записывается:

(5.4)

где - среднее зимнее термическое сопротивление снежного покрова, м²∙ ⁰С/Вт; остальные обозначения даны выше.

Подставляя (5.4) в (5.3) и решая полученное уравнение относительно будем иметь:

, (5.5)

Подставляя (5.5) в (5.2) находим охлаждающий импульс . Последний затем подставляем в (5.1) и получаем расчетную формулу для определения средней температуры вечномерзлого грунта у подошвы слоя с годовыми теплооборотами, при этом отчет температуры ведем от температуры начала замерзания грунта T_bf:

(5.6)

где - температура ВМГ при отсутствии на дневной поверхности снега, определяется по формуле (11.20), ⁰С; - температурная поправка на отепляющее влияние снежного покрова, определяется по формуле (11.21), ⁰С.

(5.7)

где принимается равной средней зимней температуре атмосферного воздуха

(5.8)

Формула (11.19) выведена для условий T₀ < T_bf. При больших снежных отложениях может оказаться, что T₀ > T_bf. Для этого случая формула выводится аналогично и имеет вид:

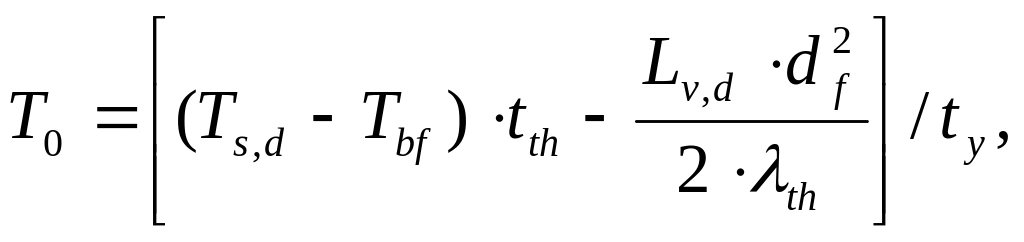(5.9)

где - средняя летняя температура поверхности грунта, ⁰С.

Задача 2. Расчет температурного поля в основании здания, возводимого с сохранением грунтов основания в мерзлом состоянии (принцип I).

Постановка задач. Рассматриваются задачи – формирования расчетных температур грунта для определения несущей способности столбчатых и свайных фундаментов. Предполагается, что процесс теплообмена в системе «здание-основание» развивается в мерзлом грунте ниже подошвы слоя сезонного оттаивания, на которой происходят гармонические колебания температуры, обусловленные условиями теплообмена выше этой подошвы. При выводе расчетных формул сделаны следующие допущения:

- длина здания значительно больше его ширины и считается бесконечной, в этом случае задача сводится к двухмерной;

- температура грунта на подошве слоя сезонного оттаивания под зданием остается постоянной по координате в пределах контура здания;

- температура грунта на подошве слоя сезонного оттаивания за зданием остается постоянной по координате вне контура здания;

- среднегодовая температура грунта на подошве слоя сезонного оттаивания под зданием определяется из условия линейной задачи т.е. считается, что ширина здания бесконечно большая.

Теоретические основы метода решения задачи. При принятых допущениях задача формулируется следующим образом:

(5.10)

начальные условия: ;

граничные условия: при .

при и .

где - коэффициент температуропроводности мерзлого грунта, м²/ч; - время, ч; - горизонтальная координата, отсчитываемая от середины здания, м; - вертикальная координата, отсчитываемая от подошвы слоя сезонного оттаивания, м; - среднегодовые температуры грунта на подошве слоя сезонного оттаиванитя внутри и вне контура здания, ⁰С; - амплитуды колебаний температуры грунта на подошве слоя сезонного оттаивания внутри и вне контура здания, ⁰С; - частота колебаний, рад/ч; - период колебаний, равный одному году, 8760 ч; - начальная фаза колебаний, рад; - ширина здания, м.

Решение уравнения (5.10) дается Г.В. Порхаевым (1970) в виде двух функций, одна из которых (*) описывает формирование средних годовых температур, а другая (**) сезонные колебания температуры вокруг своего среднегодового значения Далее Г.В. Порхаев утверждает, что одного зимнего сезона достаточно, чтобы в дальнейшем сезонные колебания принимать для установившегося периодического температурного режима, учитывая лишь изменения средних годовых температур. Однако и здесь по прошествии 3-5 лет температура достигает своего стационарного состояния и в целом под зданием устанавливается квазистационарный температурный режим, для которого полученное решение значительно упрощается и принимает вид.

Для середины здания:

(5.11)

Для края здания:

(5.12)

где .

Теперь перейдем к определению расчетных температур грунта: максимальной температуры под подошвой столбчатого фундамента , эквивалентной температуры по поверхности свайного фундамента и расчетной температуры на глубине z для столбчатого и свайного фундаментов .

Своего максимального значения на глубине заложения фундамента температура грунта под серединой и краем здания достигают, как следует из выражений (13.2) и (13.3), при значении синуса равным единице. Известно, что

амплитуда колебаний температуры на подошве слоя сезонного оттаивания за контуром здания (в естественных условиях) равна , естественно предположить, что , поскольку определение исходит из допущения, что . С учетом сказанного перепишем выражения (5.11) и (5.12).

Максимальная температура под серединой здания:

(5.13)

Максимальная температура под краем здания:

(5.14)

где - глубина заложения подошвы фундамента, отсчитываемая от подошвы слоя сезонного оттаивания, м.

Для облегчения расчетов выражения (5.13) и (5.14) записаны в виде формул (1.4) и (1.5), где параметры табулированы. Сравнивая выражения (5.13) с (4.4) и (5.14) с (1.5) легко показать, что:

; ; .

Как отмечалось выше под эквивалентной температурой понимается температура, определяющая минимальную несущую способность свайного фундамента по боковой поверхности. Известно, что сопротивление мерзлого грунта сдвигу прямо пропорционально квадратному корню из его абсолютной температуры. Однако Г.В. Порхаевым показано, что без большой погрешности для значений эквивалентной температуры параболическая зависимость может быть заменена линейной. В этом случае эквивалентная температура равна средней температуре грунта в пределах боковой поверхности сваи при минимальном значении площади эпюры температур.

Так, например, для середины здания можно записать:

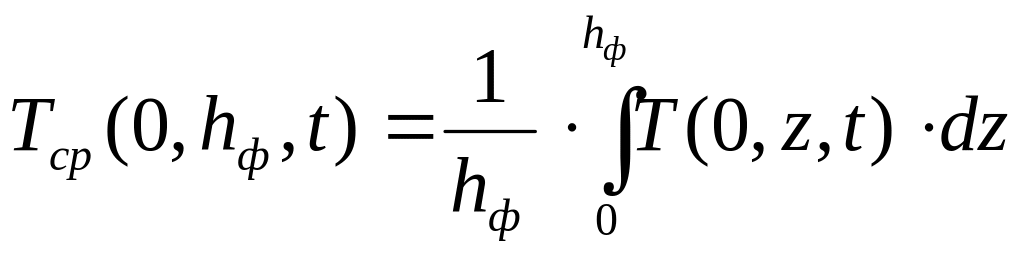. (5.15)

при минимальном абсолютном значении интеграла в правой части выражения (5.15).

Подставляя значение (5.11) в (5.15) интегрируя и преобразуя полученный результат, будем иметь:

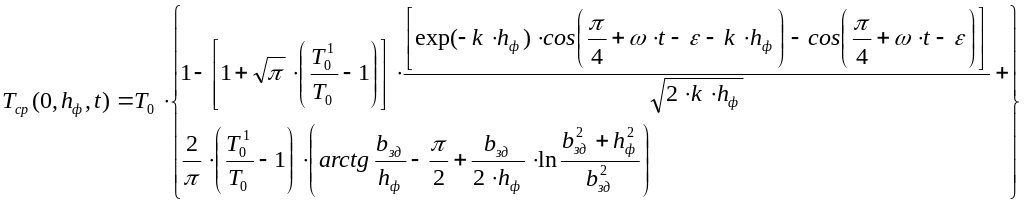(5.16)

Время, при котором абсолютное значение средней температуры будет минимальным, найдем из уравнения:

(5.17)

После дифференцирования и преобразования имеем:

, (5.18)

Подставляя из выражения (5.18) в (5.16), получим значение эквивалентной температуры , а в уравнение (5.10) – значение расчетной температуры под серединой здания. Аналогично вычисляются и для края здания.

Для облегчения расчетов этих температур составлены формулы (1.4) и (1.5), в которых параметры табулированы.

Задача 3. Pасчет среднегодовой температуры воздуха в подполье и модуля вентиляции холодного подполья здания

Постановка задач. Рассматриваются две задачи - формирование температуры воздуха в вентилируемом подполье и назначение режима вентиляции, обеспечивающего заданную температуру грунта на подошве слоя сезонного промерзания-оттаивания под зданием.

При постановке первой задачи предполагается равенство температуры поверхности грунта и воздуха в подполье, равенство температуры воздуха в подполье и температуры наружного воздуха в летний период, кроме того допускается, что в период сезонного промерзания-оттаивания грунта под зданием температура грунта на подошве слоя сезонного оттаивания равна нулю градусов.

При постановке второй задачи считается, что среднегодовым потоком тепла из грунта (в грунт) можно пренебречь ввиду его малости по сравнению с потоками тепла через перекрытие подполья, цоколь здания и вентиляционные отверстия в цоколе.

Теоретические основы метода решения задачи 1. Рассматривается задача определения температуру воздуха в подполье по известной расчетной температуре грунта . При этом за расчетную температуру грунта принимается температура грунта на глубине нулевых годовых теплооборотов, которая сформировалась бы, если размеры подполья были бы бесконечно большими. Эта температура задается нормами (СНиП 2.02.04-88) в зависимости от наружной температуры воздуха и температуры вечномерзлого грунта в районе строительства. Вначале предположим, что , тогда среднегодовая температура воздуха в подполье может быть определена из выражения (5.19).

(5.19)

где - сумма градусочасов температуры воздуха в подполье в зимний и летний периоды; - коэффициенты теплопроводности грунта слоя сезонного промерзания-оттаивания в талом и мерзлом состоянии, Вт/(м∙⁰С), - продолжительность года, 8760 ч.

Прибавив и отняв от левой части выражения (5.19) и сгруппировав члены получим:

, (5.20)

Принимая во внимание, что а окончательно запишем:

(5.21)

где – среднелетняя температура наружного воздуха, ⁰С; - продолжительность летнего периода, ч.

Далее предположим, что , тогда среднегодовая температура воздуха в подполье может быть определена из выражения (5.22).

(5.22)

Из выражения (5.22) найдем неизвестную сумму градусочасов температуры воздуха в подполье в зимний период через сумму градусочасов в летний и сумму градусочасов расчетной температуры за год:

(5.23)

Далее преобразуем выражение (5.22) как было преобразовано выражение (5.19) и найдем среднегодовую температуру воздуха в подполье:

(5.24)

Подставив вместо неизвестной величины ее значение из выражения (5.23), окончательно получим:

. (5.25)

Теоретические основы метода решения задачи 2. Рассматривается задача определения модуля вентиляции холодного подполья М по заданной среднегодовой температуре воздуха в подполье . Под модулем вентиляции понимается отношении суммарной площади вентиляционных отверстий в цоколе здания к площади пятна здания . Модуль вентиляции найдем из уравнения баланса тепла , поступающего и уходящего из подполья за год. Тепло в подполье поступает от здания и от расположенных в подполье санитарно-технических коммуникаций. Уходит из подполья через цоколь здания и выносится вентиляционным потоком. Уравнение теплового баланса вентилируемого подполья за годовой период может быть записано:

(5.26)

где - поток тепла из здания, поток тепла через цоколь здания, поток тепла, выносимого из подполья вентиляцией, поток тепла, выделяемого санитарно-техническими коммуникациями, Вт∙ч.

Величины тепловых потоков определяются по формулам:

(5.27)

где – температура воздуха в здании, ⁰С; - площадь пятна здания, м²; - термическое сопротивление перекрытия над подпольем, м²∙⁰С/Вт.

(5.28)

где – среднегодовая температура наружного воздуха, ⁰С; - площадь цоколя здания, м²; - термическое сопротивление цоколя, м²∙⁰С/Вт (5.29)

где М – модуль вентиляции, - теплоемкость воздуха, Вт∙ч/(м³∙⁰С); - среднегодовая скорость ветра, м/ч; -обобщенный ародинамический коэффициент, зависящий от формы здания в плане и его расположения на местности; - сумма местных аэродинамических сопротивлений воздуховода (вентиляционного отверстия).

(5.30)

где n – число трубопроводов в холодном подполье здания; - длина i–го трубопровода, м; -термическое сопротивление теплоизоляции i–го трубопровода, м∙⁰С/Вт; - температура жидкости в i–ом трубопроводе, ⁰С; - продолжительность работы i–го трубопровода в течение года, ч.

Подставляя (5.27) - (5.30) в (5.26) и решая полученное уравнение относительно М, получим:

(5.31)

где (5.32)

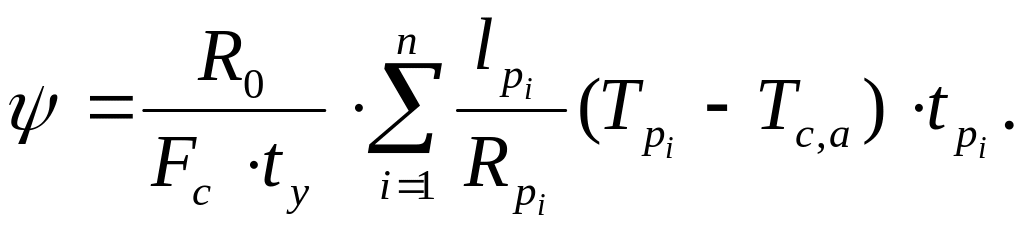(5.33)

Упростим формулу (5.31), допустив, что теплоемкость воздуха не зависит от его температуры и равна постоянной величине Вт∙ч/(м³∙⁰С), далее будем измерять скорость ветра в метеорологических единицах (м/с), введя в формулу пересчетный множитель 3600, и наконец введем в формулу эмпирический коэффициент , учитывающий расположение здания в черте застройки. С этими добавлениями формула примет окончательный вид:

(5.34)

Задача 4. Pасчет среднегодовой температуры вечномерзлого грунта на подошве слоя сезонного оттаивания под зданием, основание которого охлаждается системой труб.

Постановка задач. Рассматривается температурное поле вечномерзлого грунта под зданием, основание которого охлаждается системой труб. Трубы прокладываются в крупноскелетной подсыпке поперек здания. Требуется определить среднегодовую температуру грунта на подошве слоя сезонного оттаивания, глубину заложения труб и мощность крупноскелетной подсыпки.

При выводе расчетных формул сделаны следующие допущения:

- глубина заложения труб равна глубине сезонного оттаивания подсыпки под зданием;

- в конце зимнего периода положение нулевой изотермы (границы оттаивания) соответствует ее положению при стационарном режиме.

- в зимний период температура грунта на подошве слоя сезонного оттаивания изменяется во времени по линейному закону;

- в летний период температура грунта на подошве слоя сезонного оттаивания равна нулю;

- длина здания значительно превосходит его ширину, и задача рассматривается как двухмерная, при этом краевые эффекты теплообмена не учитываются.

Теоретические основы метода решения задачи. Вначале определим параметры температурного поля грунта в основании здания к концу зимнего периода. Расчетная схема приведена на рис. 5.2.

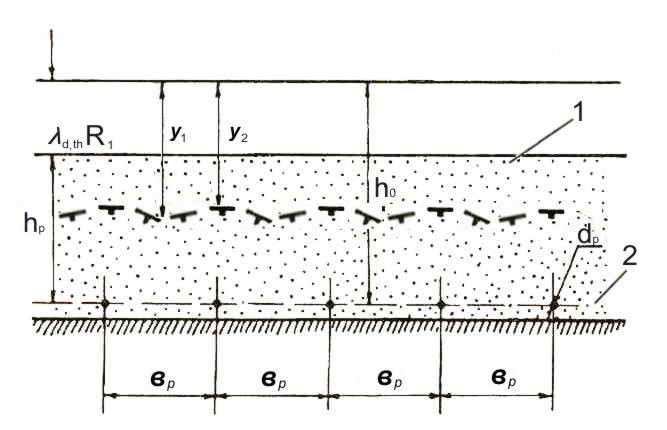
Рис. 5.2 Схема к расчету стационарного температурного поля грунта под зданием, основание которого охлаждается системой труб.

1 – талый грунт; 2 – мерзлый грунт.

Стационарное температурное поле в полуплоскости, охлаждаемое системой равностоящих цилиндрических стоков тепла описывается уравнением (Порхаев, 1970):

(5.35)

где - температура поверхности трубы, ⁰С; - температура воздуха в здании, ⁰С; - координатная функция.

, (5.36)

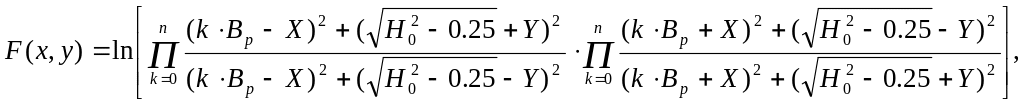(5.37)

(5.38)

где X = x / d_p, Y = y / d_p, B_p = b_p / d_p, H₀ = h₀ / d_p, h₀ = h_p + λ_d,th∙R₁, d_p – диаметр труб, м; b_p – расстояние между трубами, м; h_p – глубина заложения труб, м; R₁- термическое сопротивление пола здания с учетом термического сопротивления теплообмену на поверхности пола, м²∙⁰С/Вт; λ_d,th – коэффициент теплопроводности крупноскелетной подсыпки в талом состоянии, Вт/(м∙⁰С).

Положив из уравнения (5.35) получим выражение для для глубины залегания границы оттаивания под зданием на конец зимнего периода.

При (над трубами) это выражение принимает вид:

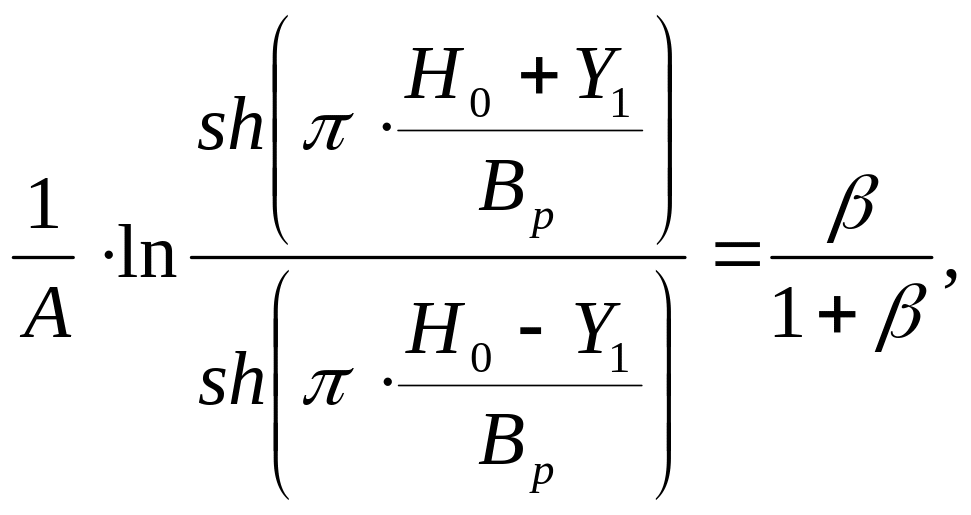(5.39)

где - безразмерная температура; ; - глубина оттаивания над центром труб, считая от условной дневной поверхности (см. рис. 5.2), м.

(5.40)

где λ_d,f – коэффициент теплопроводности крупноскелетной подсыпки в мерзлом состоянии, Вт/(м∙⁰С).

При x = b_p / 2 (между трубами) имеем:

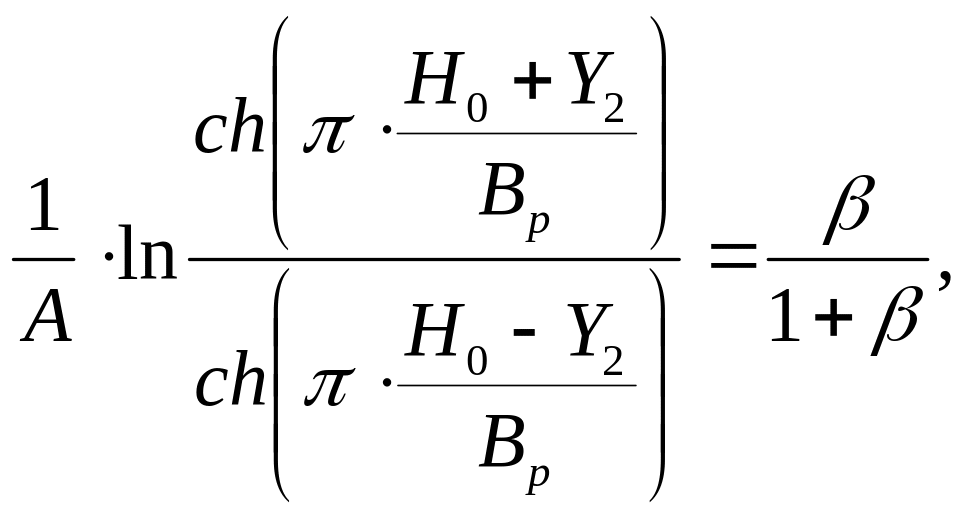(5.41)

где ; - глубина оттаивания по центру между трубами, считая от условной дневной поверхности (см. рис. 5.2), м.

С достаточной для практических расчетов точностью можно принять гиперболический синус равным в этом случае можно решить уравнение (5.30) относительно :

. (5.42)

Для вычисления безразмерной температуры необходимо знать температуру поверхности трубы , которая для труб, вентилируемых наружным воздухом принимается равной полусумме температур воздуха на входе (принимается равной среднезимней температуре атмосферного воздуха ) и выходе (принимается равной ) из трубы:

(5.43)

где - повышение температуры воздуха по мере его движения по трубе, зависит от его скорости и для воздушных систем допускается принимать 5 ⁰С.

Температура подземного теплообменника для жидкостных и парожидкостных термосифонов определяется из балансового уравнения: ( - количество тепла, поступающего из грунта к 1 п.м. подземного теплообменника в единицу времени; - количество тепла, отводимое от 1 п.м. подземного теплообменника в единицу времени его надземным теплообменником.)

(5.44)

(5.45)

где k_h – безразмерный коэффициент, учитывающий снижения тепловосприятия термосифонов в результате их горизонтального расположения, определяется по данным табл. 1.8; - температура надземного теплообменника, принимается равной среднезимней температуре атмосферного воздуха с поправкой на разогрев , последняя считается равной 1 ⁰С; R_in – внутреннее термическое сопротивление термосифона теплообмену, определяемое для парожидкостных термосифонов по формуле (1.7), для жидкостных термосифонов – по формуле (1.9), м^{2 0}С / Вт.

Приравняв (5.44) к (5.45) и решив полученное уравнение относительно , получим:

(5.46)

где - критерий Био: (5.47)

Средняя температура грунта на уровне заложения труб к концу зимнего периода в общем случае определяется по формуле:

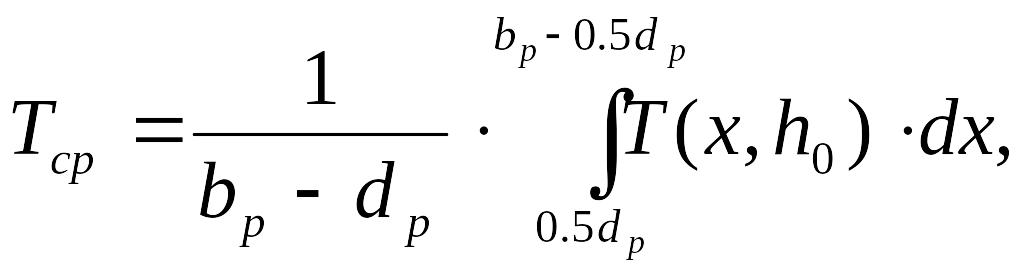(5.48)

Однако, если предположить, что нулевая изотерма (фазовая граница) располагается параллельно дневной поверхности на глубине , то можно определить из условия равенства теплопотока, приходящего к нулевой изотерме и уходящего от нее:

(5.49)

Очевидно, что глубина должна находится в интервале глубин и . С запасом принимаем (в этом случае значение будет максимально) и из подобия треугольников на рис. 13.2 находим искомую температуру:

(5.50)

Неизвестную глубину находим по формуле Стефана, т.к. согласно допущению трубы лежат на подошве слоя сезонного оттаивания под зданием:

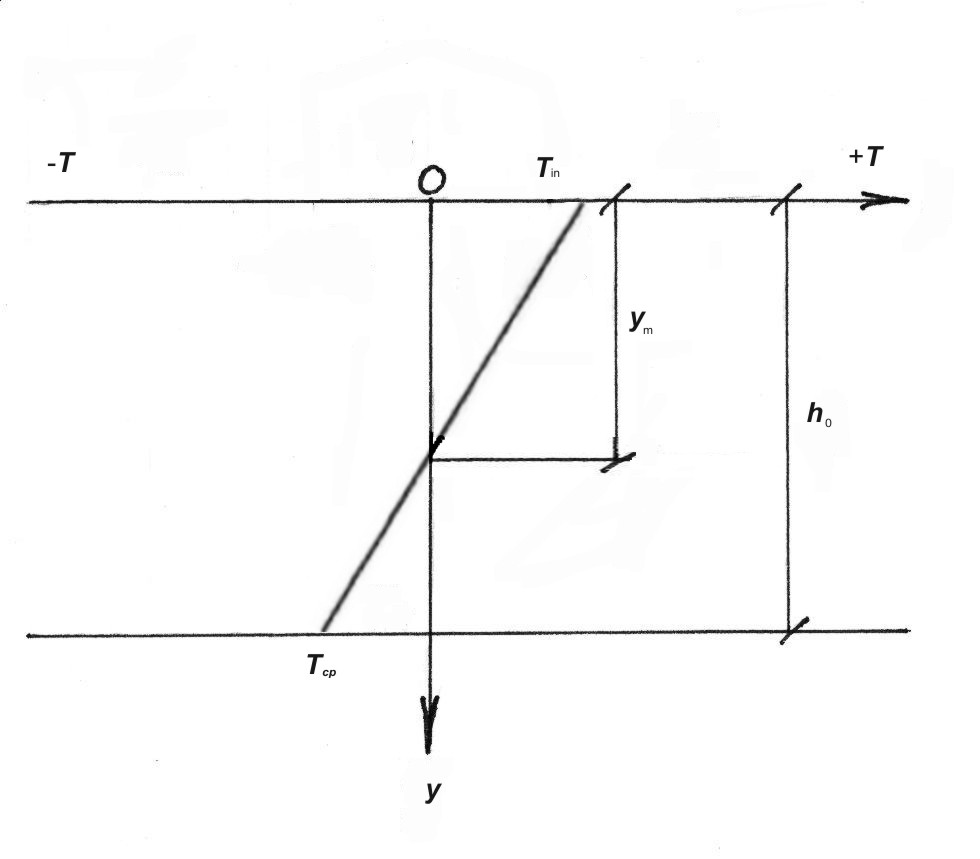
Рис. 5.3 Схема к определению средней температуры грунта на уровне заложения труб.

(5.51)

где - продолжительность летнего периода, ч; L_d,v - удельные затраты тепла на оттаивание подсыпки, определяются по формуле (1.23), Втч/м³.

Средняя годовая температура грунта на подошве слоя сезонного оттаивания под зданием вычисляется по формуле:

(5.52)

где - среднегодовая, среднелетняя и среднезимняя температура на подошве слоя сезонного оттаивания под зданием, ⁰С; - продолжительность зимнего периода и

года, ч.

Согласно сделанным допущениям и Последнее выражение соответствует допущению о линейном изменении температуры грунта на подошве слоя сезонного оттаивания в зимний период от 0 до Тогда окончательно получаем:

(5.53)

В результате имеем систему совместных уравнений (5.41), (5.50), (5.51) и (5.53), решая которую находим неизвестные значения . На этом расчет термосифонов заканчивается, а для вентиляционных труб дополнительно определяется необходимая минимальная скорость движения в них атмосферного воздуха.

Вынос тепла одной вентиляционной трубой определяется по формуле:

(5.54)

где - объемная теплоемкость воздуха, Вт∙ч/(м³∙⁰С); - скорость движения воздуха, м/ч.

Приток тепла к трубе из грунта будет равен:

(5.55)

где - теплопоток, определяемый по формуле (5.35), Вт/м; - ширина здания (трубы расположены поперек здания), м.

Кроме того к трубе поступает тепло от промерзающего грунта:

(5.56)

Приравняв сумму теплопотоков, поступающих к трубе, к теплопотоку, выносимому трубой, получим уравнение, из которого найдем необходимую скорость движения в трубе воздуха:

(5.57)

Задача 5. Расчет глубины оттаивания вечномерзлого грунта под зданием с полами по грунту.

Постановка задачи. Рассматривается оттаивание вечномерзлого грунта сливающегося типа под зданием. Процесс происходит во времени от начала эксплуатации здания.

Требуется определить на любой заданный момент времени t форму границы между талой и мерзлой зонами грунта. При выводе расчетных формул сделаны следующие допущения:

- длина здания значительно больше его ширины и считается бесконечной, в этом случае задача сводится к двухмерной;

- граница оттаивания (фазовая граница) перемещается по изотермам стационарного состояния;

- в каждый момент времени температурные поля в талой и мерзлой зонах грунта стационарны;

- сезонное промерзание-оттаивание за контуром здания не учитывается;

- за расчетную температуру на поверхности грунта под зданием принимается температура поверхности пола T₁, вне здания – температура вечномерзлого грунта на глубине нулевых годовых теплооборотов в естественных условиях T₂.

Теоретические основы метода решения задачи. Вначале запишем решение стационарного температурного поля в полуплоскости, на границе которой заданы многочисленные источники и стоки тепла. Эта задача формулируется следующим образом:

. (5.58)

Граничные условия:

Она известна как первая краевая задача Дирихле и ее решением является следующее выражение (см., например, Смирнов, 1959):

(5.59)

Если кусочная, то выражение (13.41) преобразуется:

(5.60)

где n – число теплоисточников и стоков тепла на полуплоскости, - температура источника или стока тепла на i–ом участке границы, ⁰С; - координатная функция i–го участка, при этом сумма всех координатных функций равна единице

(5.61)

где - координаты левой и правой границы i–го участка, м; - текущие координаты, м.

Пользуясь выражением (5.60) запишем формулу для определения стационарного температурного поля в основании здания (рис.5.4):

(5.62)

По формуле (13.43) определяем координатную функцию:

(5.63)

где - ширина здания, м.

Стационарное температурное поле внутри и снаружи любой изотермы под зданием может быть записано через численное значение этой изотермы, температуры на границе и координатные функции. Проделаем эту операцию применительно к изотерме, численное значение которой равно .

Температурное поле внутри изотермы : . (5.64)

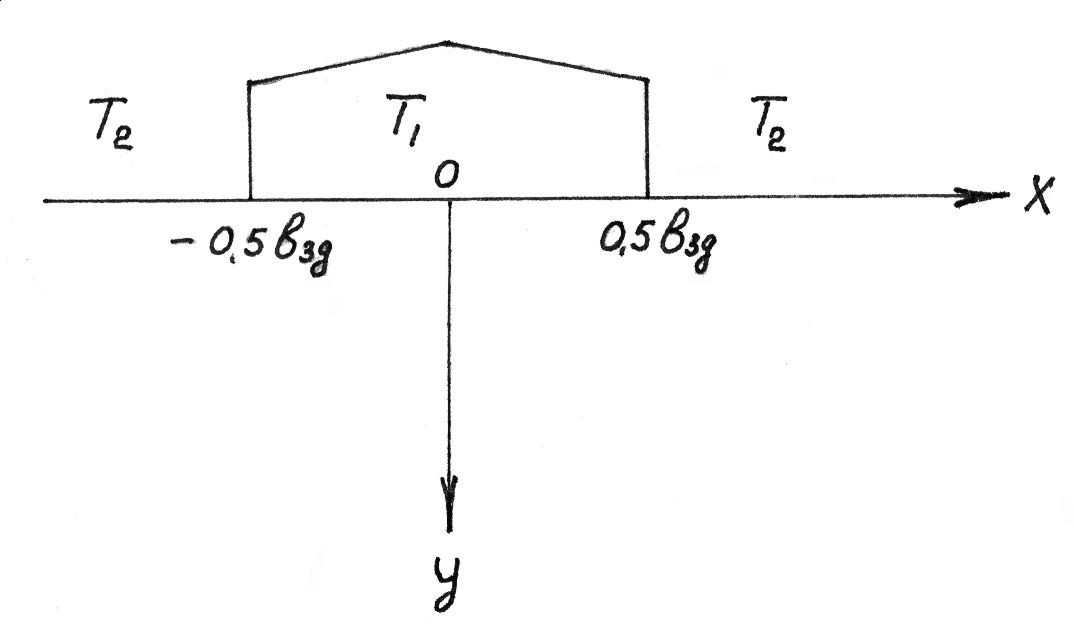
Рис. 5.4 Схема к определению стационарного температурного поля под полосообразным теплоисточником, расположенным на полуплоскости.

Температурное поле снаружи изотермы : . (5.65)

Значение изотермы запишем через одну из ее координат, например :

(5.66)

Выразим неизвестные координатные функции через известные и .

Вначале проделаем эту операцию для координатных функций и . Поскольку выражение (5.62) и (5.64) описывают одно и то же температурное поле, то их можно приравнять, предварительно подставив значение из выражения (5.57). В результате получим: (5.67)

Равенство (5.67) означает, что коэффициенты при одних и тех же температурах равны между собой, т.е.:

(5.68)

Решая систему уравнений (5.68), получим:

Аналогично находим координатные функции :

Зная координатные функции , перепишем выражения (5.64) и (5.65).

Температурное поле внутри изотермы :

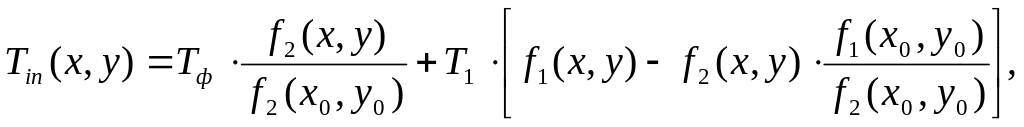(5.69)

Температурное поле снаружи изотермы :

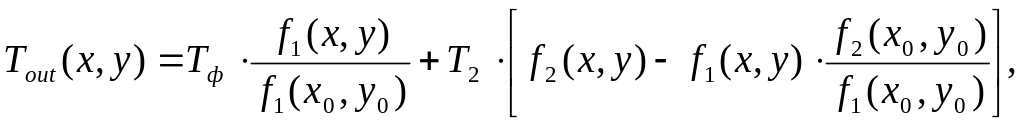(5.70)

Теперь перейдем к рассмотрению нестационарного температурного поля. Предположим, что изотерма есть граница оттаивания (граница оттаивания перемещается по изотермам стационарного состояния), тогда ( - температура фазового перехода лед-вода) и выражение (5.69) описывает температурное поле в талой зоне основания здания, а выражение (5.70) – в мерзлой. Запись можно упростить, если отсчет температуры вести не от 0, а от . С учетом этого перепишем выражения (5.69) и (5.70), имея в виду, что :

, (5.71)

, (5.72)

где и - распределение температуры в талой и мерзлой зонах основания здания, отсчитываемые от .

Зная температурные поля в талой и мерзлой зонах основания, из уравнения теплового баланса найдем перемещение фазовой границы:

(5.73)

где – количество тепла, приходящее к фазовой границе из талой зоны (от здания), Вт/м²; - количество тепла уходящее в мерзлую зону, Вт/м²; - количество тепла, идущее на фазовые переходы грунтовой влаги, Вт/м².

Для середины здания в силу симметрии задачи уравнение (5.73) перепишется особенно просто:

, (5.74)

где - коэффициенты теплопроводности талого и мерзлого грунта в основании здания, Вт/(м∙⁰С); L_v – удельная теплота таяния мерзлого грунта, определяется по формуле (4.6), Втч / м³; t – время, ч.

Разделяя переменные, переходя к безразмерной координате и интегрируя, окончательно получим:

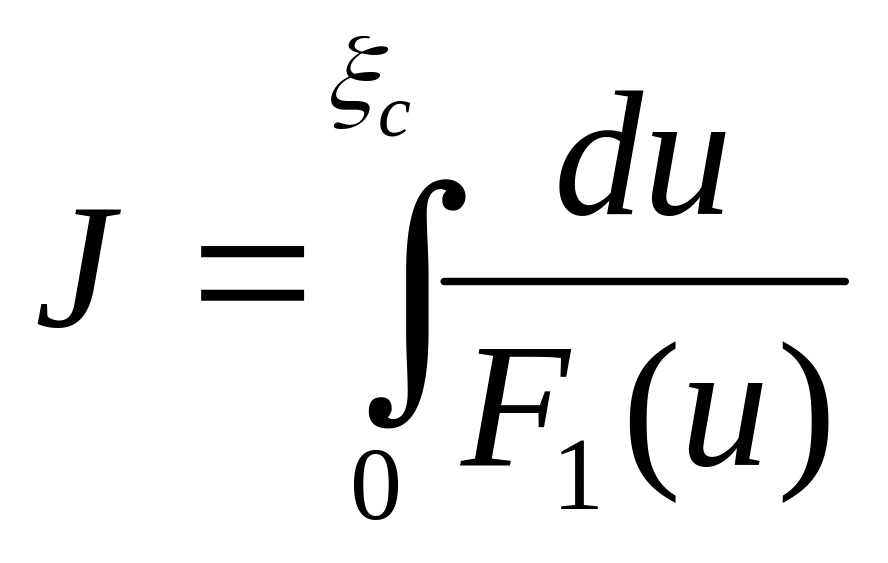, (5.75)

где J- безразмерное время, определяется по формуле (5.76); - безразмерная глубина оттаивания под серединой здания ; - глубина оттаивания под серединой здания, м; - безразмерная функция, определяется по формуле (5.77).

. (5.76)

(5.77)

где - безразмерная температура, определяется по формуле (13.69).

. (5.78)

Интеграл в выражении (5.75) вычисляется численным методом.

После того как глубина оттаивания под под серединой здания найдена, можно определить форму чаши оттаивания. Из допущения о перемещении границы оттаивания во времени по изотермам стационарного состояния следует, что если граница оттаивания проходит через некоторую точку с координатами ( , то форма чаши оттаивания будет описываться уравнением: Задавая, например, точку ( на границе чаши оттаивания под серединой здания получим:

, (5.79)

Это уравнение легко привести к виду:

, (5.80)

где 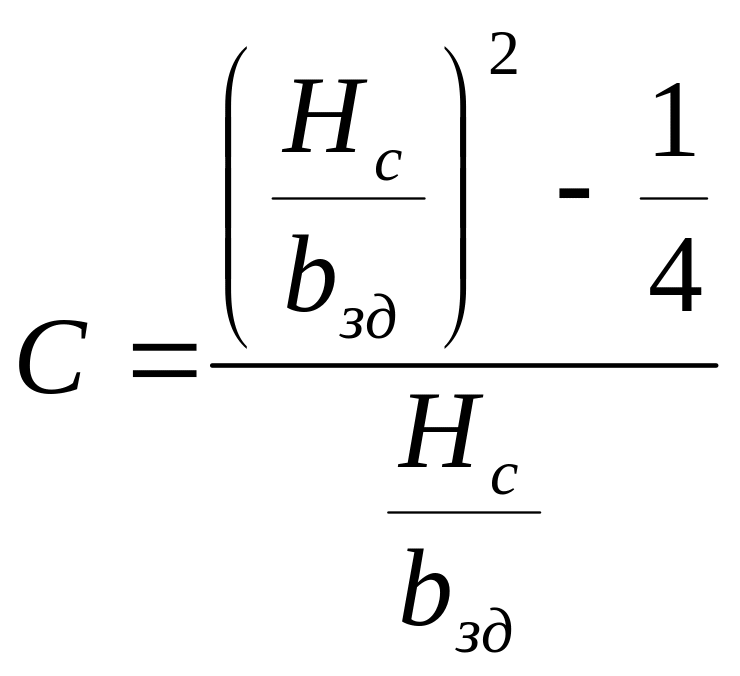, (5.80)

Уравнение (5.80) описывает окружность с радиусом и центром, расположенным под (над) серединой здания на глубине (высоте) (рис. 5.5).

Рис. 5.5 Графическое построение формы чаши оттаивания под зданием на вечномерзлых грунтах сливающегося типа.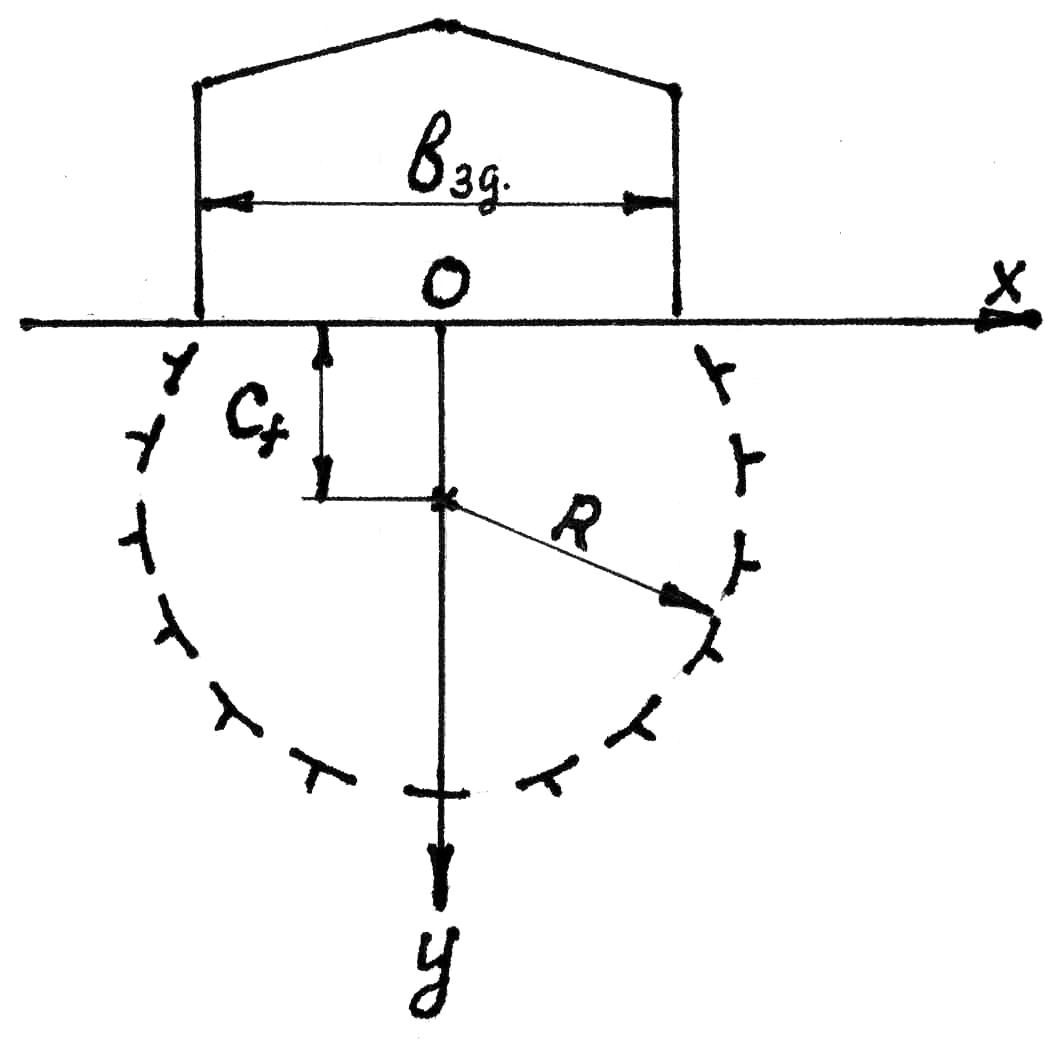

Из уравнения, описывающего форму чаши оттаивания, легко получить, что глубина оттаивания под краем здания при и при .

Задача 6. Расчет ореола оттаивания вечномерзлого грунта вокруг подзем ного трубопровода.

Постановка задачи. Рассматривается оттаивание вечномерзлого грунта вокруг цилиндрического теплоисточника. Требуется определить на любой заданный момент времени t форму границы между талой и мерзлой зонами грунта. При выводе расчетных формул сделаны следующие допущения:

- длина теплоисточника считается бесконечной, в этом случае задача сводится к двухмерной;

- граница оттаивания (фазовая граница) перемещается по изотермам стационарного состояния;

- в каждый момент времени температурные поля в талой и мерзлой зонах грунта стационарны;

- сезонное промерзание-оттаивание грунта не учитывается;

- за расчетную температуру на внутренней поверхности трубы принимается температура теплоносителя (газ, жидкость) , на поверхности грунта – температура вечномерзлого грунта на глубине нулевых годовых теплооборотов в естественных условиях T₀;

- температура внешней поверхности трубопровода с изоляцией или внешней поверхности горизонтальной горной выработки с крепью постоянна по всей поверхности.

Теоретические основы метода решения задачи. Вначале запишем решение стационарного температурного поля в полуплоскости с круговым вырезом (рис. 5.6), на границе выреза и поверхности плоскости заданы постоянные температуры. Задача формулируется следующим образом:

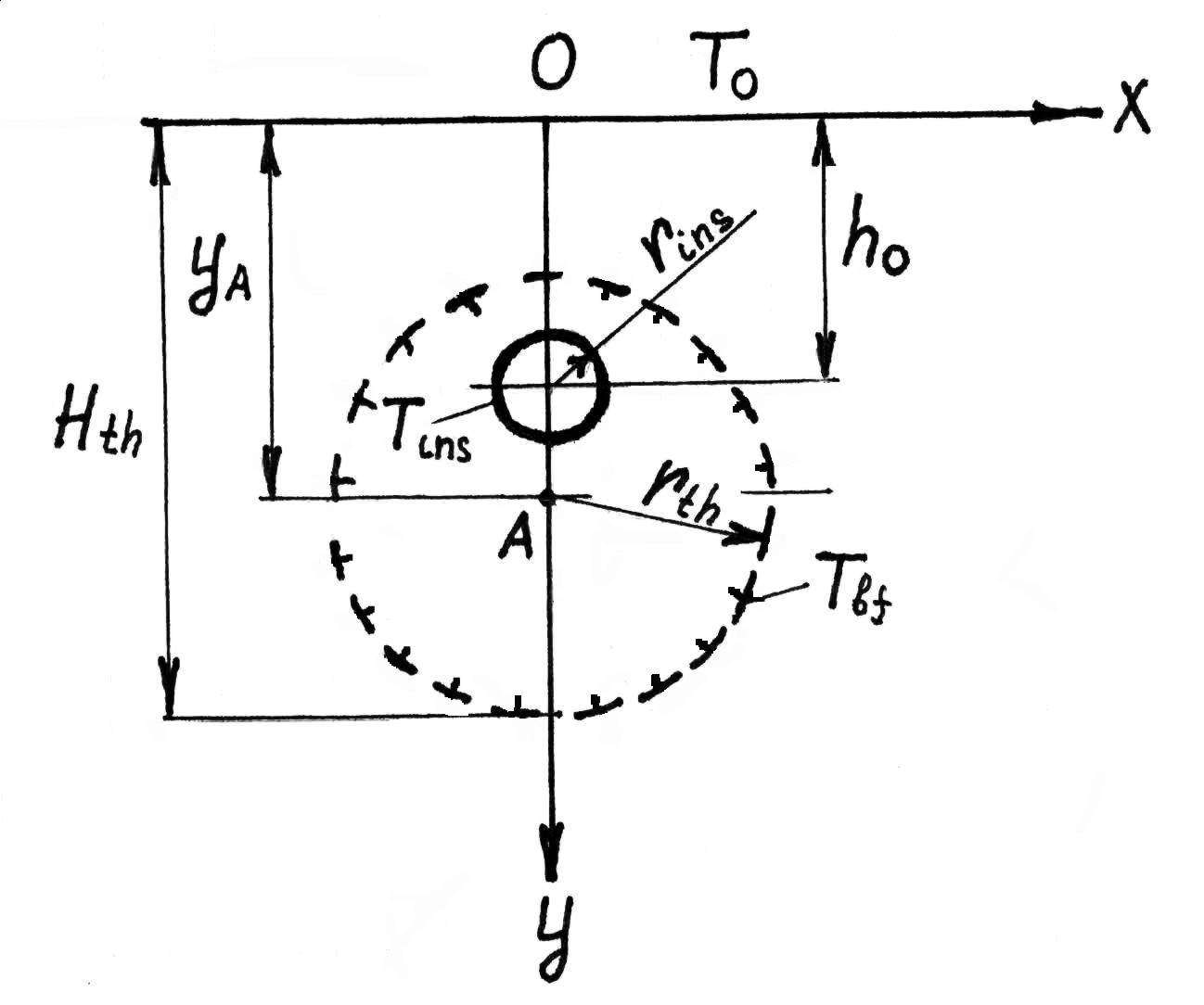
Рис. 5.6 Схема к расчету ореола оттаивания вечномерзлых грунтов вокруг подземного трубопровода

(5.81)

Граничные условия: , , (5.82)

где - координаты внешней поверхности трубопровода, м.

Решением задачи является уравнение Форхгеймера (Шорин, 1964), которое запишем через координатные функции:

, (5.83)

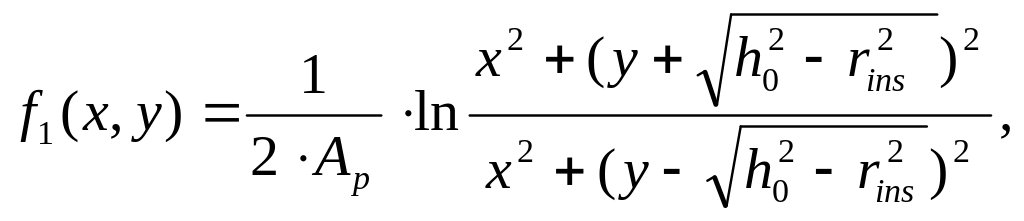(5.84)

(5.85)

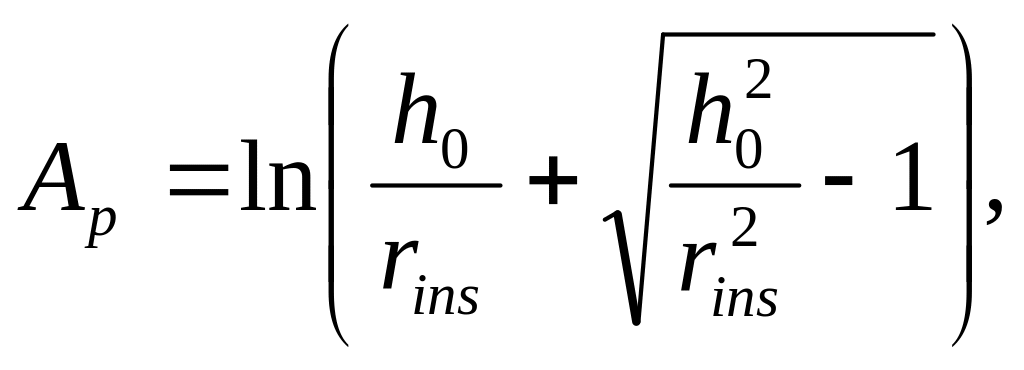(5.86)

где – глубина заложения трубопровода (горной выработки), считая от поверхности грунта, м; - радиус трубопровода (горной выработки) с учетом толщины изоляции (крепи), м.

Согласно решению Форхгеймера теплопоток от кругового теплоисточника будет равен:

(5.87)

где - коэффициент теплопроводности грунта (средний между его талым и мерзлым состоянием), Вт/(м∙⁰С).

С другой стороны теплопоток от перемещаемого газа или жидкости с положительной температурой будет равен:

(5.88)

(5.89)

где – коэффициент теплообмена между внутренней стенкой трубопровода (выработки) и перемещаемым продуктом, определяется по формуле (5.90), Вт/(м²∙⁰С); - коэффициент теплопроводности материала изоляции трубопровода, Вт/(м∙⁰С); - внутренний радиус трубопровода, м.

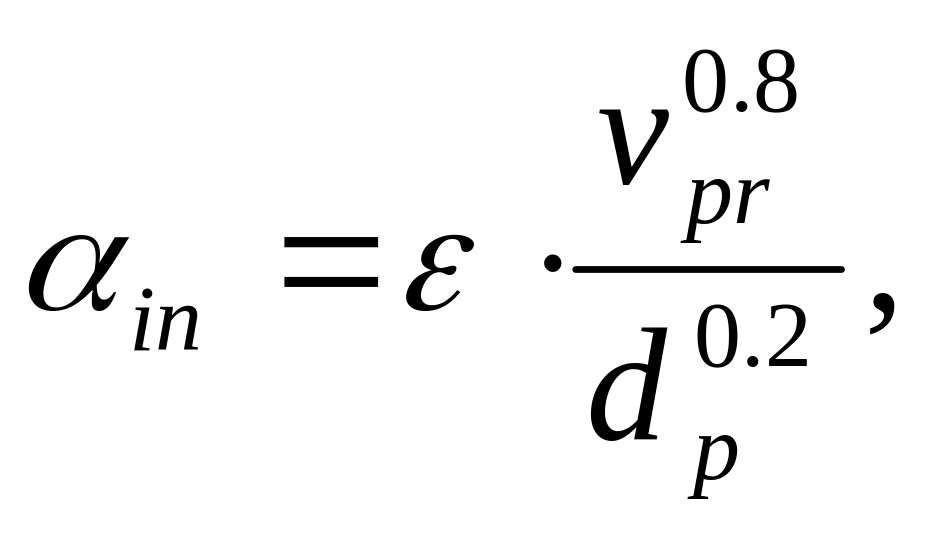(5.90)

где – эмпирический коэффициент, принимаемый для газа равным 4.67∙10^-3, для жидкости – 1220; - скорость перемещения продукта, м/с; - внутренний диаметр трубопровода (горной выработки), м.

Приравнивая теплопотоки , получим уравнение, из которого найдем неизвестную температуру внешней поверхности трубопровода:

(5.91)

Как отмечалось выше, стационарное температурное поле внутри и снаружи любой изотермы поля может быть записано через численное значение этой изотермы, температуры на границе и координатные функции. Проделаем эту операцию применительно к изотерме, численное значение которой равно .

Температурное поле внутри изотермы : . (5.92)

Температурное поле снаружи изотермы : . (5.93)

Значение изотермы запишем через одну из ее координат, например :

(5.94)

Выразим неизвестные координатные функции через известные и .

Вначале проделаем эту операцию для координатных функций и . Поскольку выражение (5.83) и (5.92) описывают одно и то же температурное поле, то их можно приравнять, предварительно подставив значение из выражения (5.94). В результате получим: (5.95)

Равенство (5.95) означает, что коэффициенты при одних и тех же температурах равны между собой, т.е.:

(5.96)

Решая систему уравнений (5.96), получим:

Аналогично находим координатные функции :

Зная координатные функции , перепишем выражения (5.41) и (5.42).

Температурное поле внутри изотермы :

(5.97)

Температурное поле снаружи изотермы :

(5.98)

Теперь перейдем к рассмотрению нестационарного температурного поля. Предположим, что изотерма есть граница оттаивания (граница оттаивания перемещается по изотермам стационарного состояния), тогда и выражение (5.97) описывает температурное поле в талой зоне основания здания, а выражение (5.98) – в мерзлой. Запись можно упростить, если отсчет температуры вести не от 0, а от . С учетом этого перепишем выражения (5.97) и (5.98), имея в виду, что :

, (5.99)

, (5.100)

где и - распределение температуры в талой и мерзлой зонах вокруг кругового теплоисточника, отсчитываемые от .

Зная температурные поля в талой и мерзлой зонах основания, из уравнения теплового баланса найдем перемещение фазовой границы:

(5.101)

где – количество тепла, приходящее к фазовой границе из талой зоны (от трубопровода или горной выработки), Вт/м²; - количество тепла уходящее в мерзлую зону, Вт/м²; - количество тепла, идущее на фазовые переходы грунтовой влаги, Вт/м².

Для середины трубопровода в силу симметрии задачи уравнение (5.101) перепишется особенно просто, т.к. линия симметрии совпадает с линией тока:

, (5.102)

где - коэффициенты теплопроводности талого и мерзлого грунта, Вт/(м∙⁰С); L_v – удельная теплота таяния мерзлого грунта, определяется по формуле (2.20), Втч / м³; t – время, ч.

Разделяя переменные, переходя к безразмерной координате и интегрируя, окончательно получим:

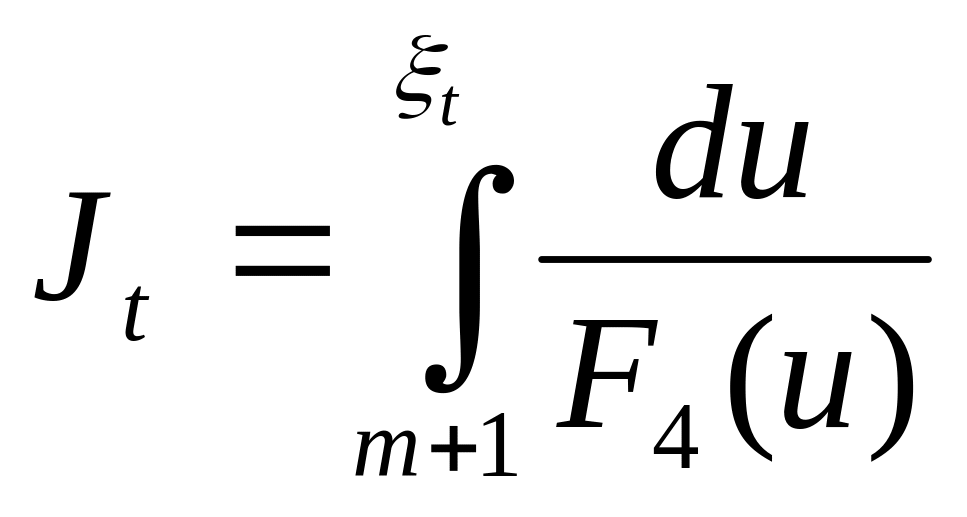. (5.103)

где - безразмерное время, определяется по формуле (5.104); безразмерная глубина оттаивания под серединой трубопровода ; - глубина оттаивания под серединой трубопровода, м; - безразмерная функция, определяется по формуле (5.105).

. (5.104)

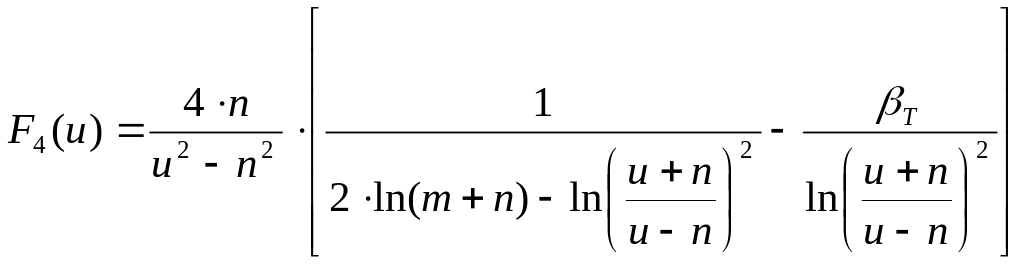, (5.105)

где , , . (5.106)

Интеграл в выражении (5.103) вычисляется численным методом.

После того как глубина оттаивания под серединой трубопровода найдена, можно определить форму ореола оттаивания. Из допущения о перемещении границы оттаивания во времени по изотермам стационарного состояния следует, что если граница оттаивания проходит через некоторую точку с координатами ( , то форма чаши оттаивания будет описываться уравнением: Задавая, например, точку ( на границе ореола оттаивания под серединой трубопровода получим:

, (5.107)

Из выражения (5.107) следует, что ореол оттаивания представляет собой круг с радиусом и центром, расположенным в точке: .

Задача 7. Расчет остывания продукта (газ, нефть) по мере его движения по трубопроводу.

Постановка задачи. Рассматривается процесс остывания продукта за счет теплопотерь в системе продукт – атмосфера (надземная прокладка трубопровода) и в системе продукт – грунт – атмосфера (подземная прокладка трубопровода). Требуется определить температуру продукта в конечной точке трубопровода, зная температуру в начальной, и наоборот по температуре в конечной точке определить температуру в начальной. Кроме того найти необходимые затраты тепла на подогрев продукта в начальной точке, чтобы обеспечить его заданную температуру в конечной.

При выводе расчетных формул сделаны следующие допущения:

- процесс теплопотерь считается стационарным, фактор времени не учитывается;

- за расчетную температуру воздуха (надземная прокладка) принимается средняя температура воздуха наиболее холодной пятидневки , за расчетную температуру поверхности грунта (подземная прокладка) – минимальная температура грунта на глубине заложения трубопровода , определяется по формуле (2.12);

- коэффициенты теплопроводности талого и мерзлого грунта равны между собой

Теоретические основы метода решения задачи. Вначале выведем расчетные формулы для определения остывания продукта. Предположим, что по мере движения продукта по трубопроводу на элементарном отрезке пути его температура понизится на элементарную величину (рис. 13.14). Это вызовет потерю тепла продуктом равную:

(5.108)

где – теплоемкость продукта, Вт∙ч/(м³∙⁰С); - расход продукта, м³/ч.

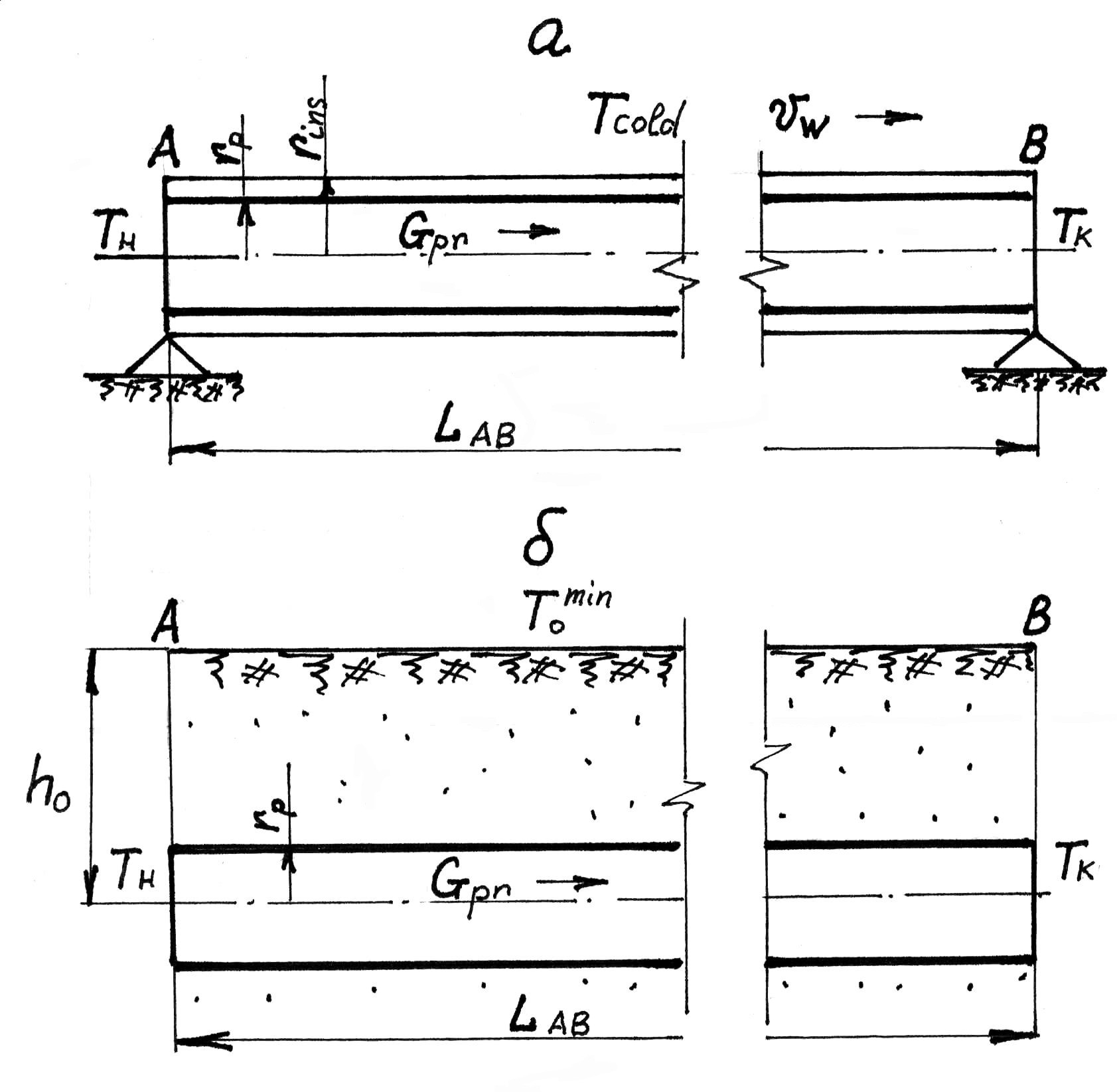
Рис. 5.7 Схема к расчету охлаждения продукта по мере его движения по надземному (а) и подземному (б) трубопроводу.

Это тепло через стенку трубопровода и теплоизоляцию поступит в атмосферу и составит величину пренебрегая малыми второго порядка, можем записать: (5.109)

где – температура продукта в начале участка , ⁰С; - расчетная температура окружающей среды, определяется по формуле (5.110); - внутреннее термическое сопротивление трубопровода (сопротивление между продуктом и поверхностью теплоизоляции), определяется по формуле (2.19), м²∙⁰С/Вт; - внешнее термическое сопротивление трубопровода (сопротивление между поверхностью изоляции и атмосферным воздухом в случае надземной прокладки и поверхностью грунта в случае подземной прокладки), определяется по формуле (5.111), м²∙⁰С/Вт.

(5.110)

(5.111)

где – максимальная скорость ветра зимой, м/с; - радиус трубопровода с учетом толщины теплоизоляции, м; - безразмерный параметр, определяемый по формуле (2.9).

Приравнивая к и разделяя переменные получим следующее дифференциальное уравнение:

(5.112)

Произведем интегрирование правой и левой части этого уравнения:

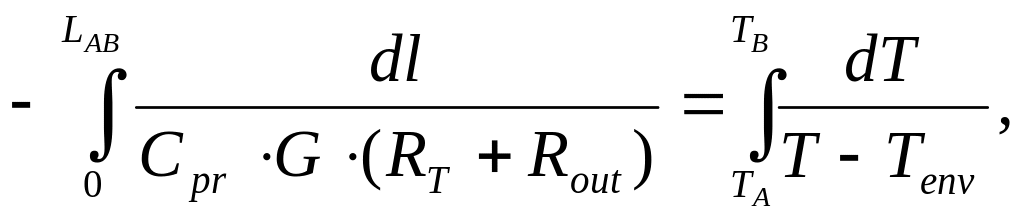
В результате будем иметь:

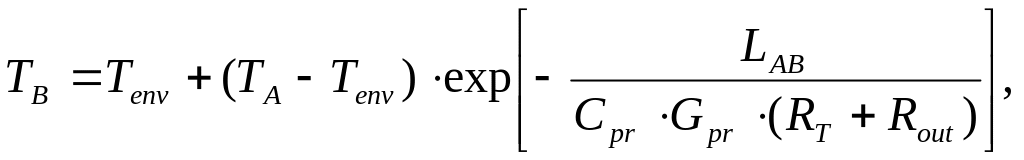(5.113)

где – температура продукта в начале трассы в точка А, ⁰С; - температура продукта в конце трассы в точке В, ⁰С, - протяженность трассы, расстояние от точки А до точки В, м.

Далее определим необходимое количество тепла, которое требуется сообщить продукту в начале трассы трубопровода, чтобы его температура в конце трассы была не ниже . Для этого перепишем выражение (5.113):

(5.114)

где - допустимая температура продукта в конечной точке трассы трубопровода, ⁰С.

Если в точках А и В находятся пункты подогрева транспортируемого продукта, то легко вычислить затраты тепла на подогрев:

(5.115)

где - интенсивность подачи тепла на подогрев транспортируемого продукта, Вт.

Задача 8. Расчет радиуса оттаивания мерзлых грунтов вокруг нефтяной или газовой скважины.

Постановка задачи. Рассматривается процесс оттаивания мерзлого грунта вокруг нефтяной или газовой скважины. Температура флюида всегда положительна, поэтому вокруг скважины образуется растущая во времени талая зона (зона 1), сопрягающаяся с мерзлой зоной (зона 2). Считается, что температура грунта в зоне 1 и зоне 2 на каждый момент времени стационарна. Тепловой поток по вертикальной координате отсутствует. Тепловое влияние скважины сказывается только на расстоянии r₂ = 6.5∙r_th от ее центра. Требуется определить радиус оттаивания вокруг скважины r_th как функцию времени t_th. Обоснование перечисленным допущениям приводится в работе Х.Р.Хакимова (1957). Расчетная схема показана на рис.5.8.

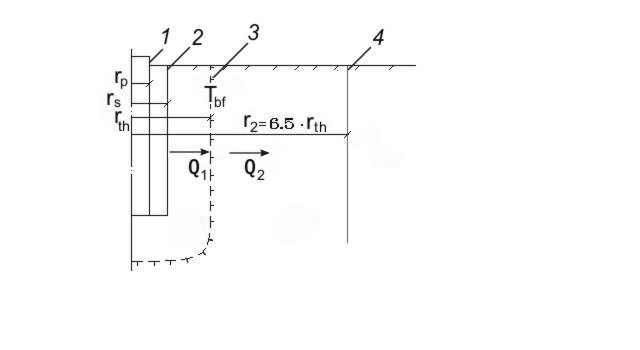
Рис. 5.8 Схема к расчету радиуса оттаивания вокруг скважины.

1 – эксплуатационная колонна труб нефтяной или газовой скважины; 2 – цементное кольцо вокруг скважины ; 3 – граница оттаивания; 4 – граница теплового влияния скважины.

Теоретические основы метода решения задачи. Поскольку мы допустили, что тепловой поток по вертикальной координате отсутствует, то тем самым превратили нашу задачу в линейную осесимметричную.

Математически она формулируется следующим образом:

при , (5.116)

при , (5.117)

где T₁(r), T₂(r) – соответственно температура грунта в талой и мерзлой зоне, ⁰С; r - текущий радиус, м; r_p, r_th, r₂ - соответственно радиус скважины, оттаивания и теплового влияния, м.

Граничные условия:

r = r_р : , (5.118)

r = r_th : , (5.119)

r = r₂ : (5.120)

где T_in – средняя по длине скважины температура флюида, ⁰С; T_bf - температура начала оттаивания грунта, ⁰С; T₀ - температура мерзлого грунта в естественных условиях, ⁰С.

Решение этого уравнения будет (см., например, Шорин, 1964):

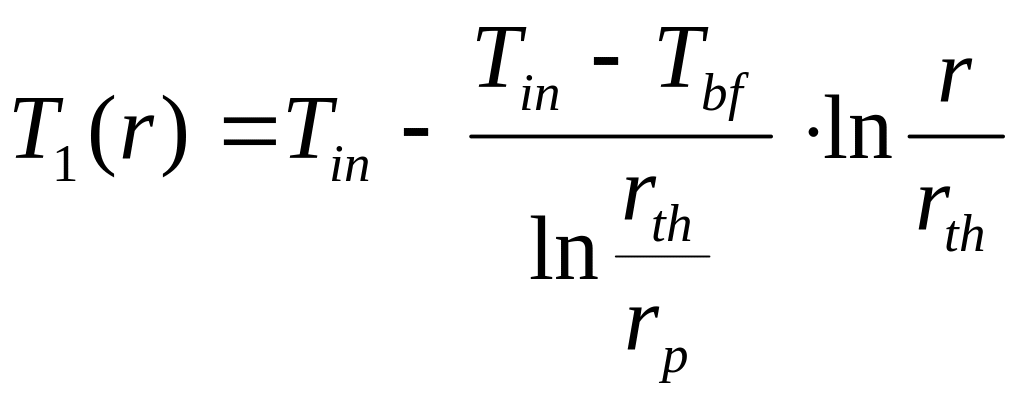, (5.121)

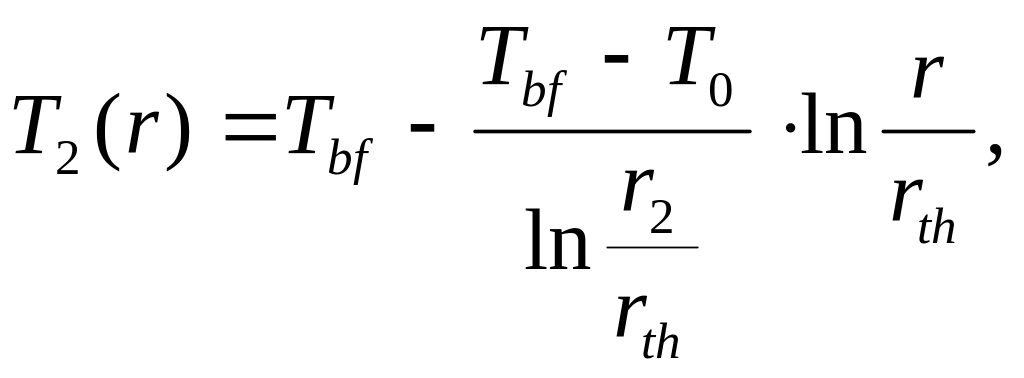(5.122)

Tаким образом, если известен радиус оттаивания, то известно и температурное поле в зонах 1 и 2. Найдем этот радиус из калориметрического уравнения Стефана:

(5.123)

где – соответственно количество тепла, поступающего к границе оттаивания от скважины, количество тепла, уходящего от границы оттаивания в мерзлую зону, количество тепла, поглощаемое грунтом при оттаивании находящегося в нем льда, Вт∙ч.

Для определения и вначале вычислим интенсивность потоков. Интенсивность теплового потока по всей длине границы оттаивания будет равна:

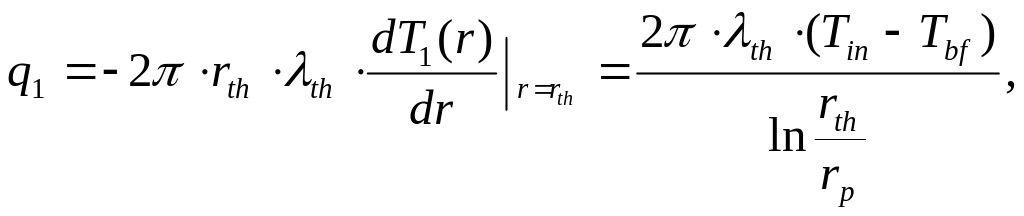(5.124)

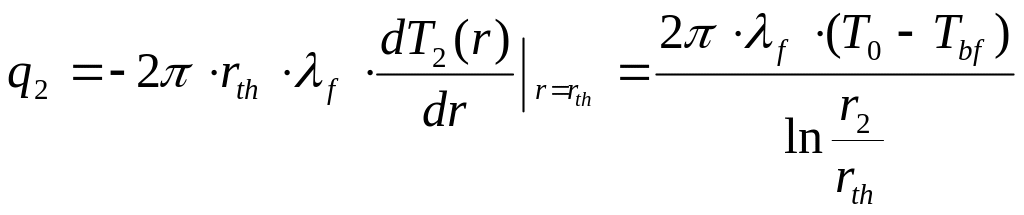или учитывая, что , можем записать: (5.125)

где , – коэффициент теплопроводности талого и мерзлого грунта, Вт/(м∙⁰С).

Величину найдем как произведение средней интенсивности теплового потока q₁ за расчетный период на величину периода:

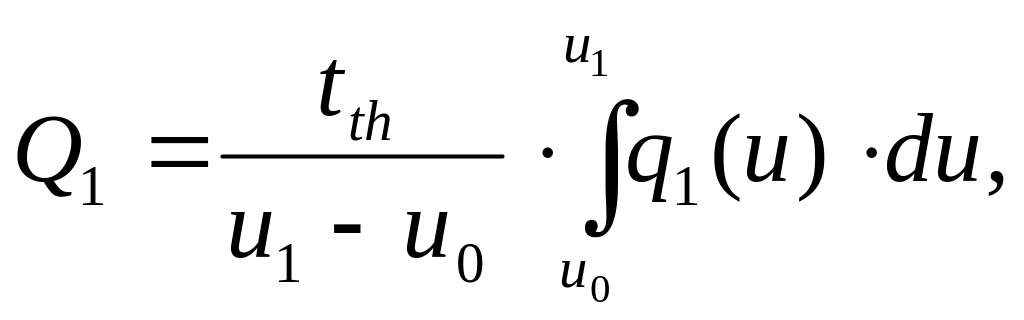(5.126)

где u = r / r_p, u₁ = r_th / r_p, u₀ = r_s / r_p, r_s – радиус бетонного кольца вокруг скважины, м.

Произведя интегрирование, получим:

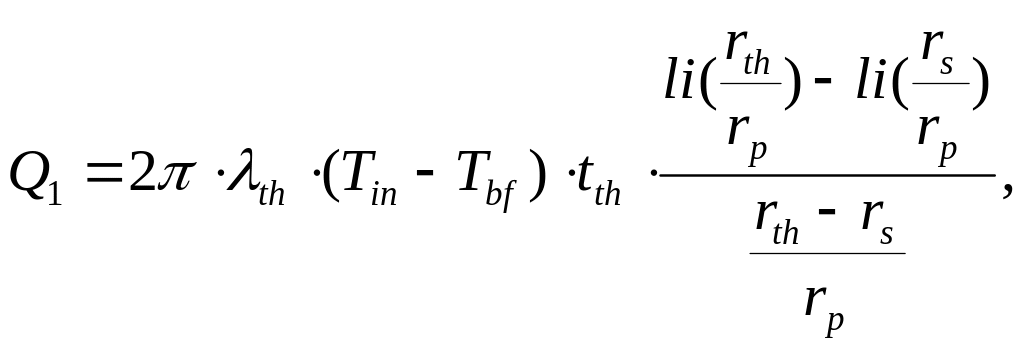(5.127)

Аналогично выводится формула для величины Q₂, опуская вывод, запишем окончательный результат:

(5.128)

Величина Q_ф определяется как произведение площади мерзлой зоны на удельную теплоту, поглощаемую при оттаивании грунта:

(5.129)

где L_v – удельная теплота, поглощаемая при оттаивании грунта, определяется по формуле (4.6), Вт∙ч/м³.

Подставляя (5.127), (5.128), (5.129) в (5.123), получим формулу, связывающую время оттаивания с радиусом оттаивания:

, (5.130)

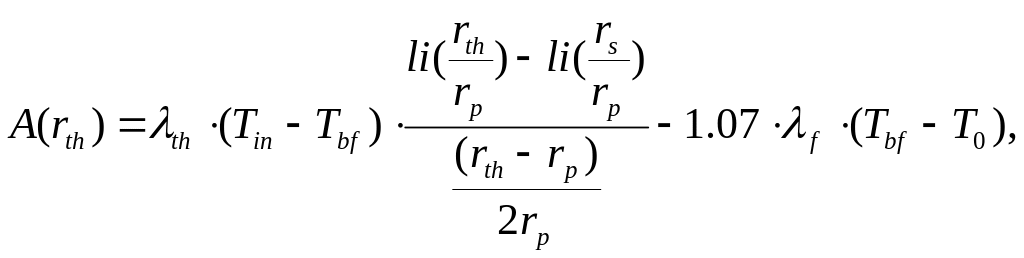(5.131)